Inhaltsverzeichnis
Dieser Anhang enthält einige häufig genutzte Tabellen für fünf wichtige Verteilungen für die weiterführende Statistik: die t-Verteilung, die Binomialverteilung, die Chi-Quadrat-Verteilung, die Verteilung für den Rangsummentest und die F-Verteilung.
zeigt rechtsseitige Wahrscheinlichkeiten für die t-Verteilung (siehe Kapitel 3). Um verwenden zu können, benötigen Sie vier Informationen über die Aufgabenstellung, die Sie bearbeiten:
Die Stichprobengröße (n) Den Mittelwert von x (für eine gegebene Normalverteilung) Die Standardabweichung Ihrer Daten (s) Den Wert von x, für den Sie die rechtsseitige Wahrscheinlichkeit ermitteln wollenNachdem Sie diese Information besitzen, wandeln Sie Ihren x-Wert in eine t-Statistik (oder einen t-Wert) um, indem Sie von Ihrem x-Wert den Mittelwert subtrahieren und dann durch den Standardfehler dividieren (siehe Kapitel 3). Dazu verwenden Sie die Formel 
Anschließend schlagen Sie diesen Wert von t in nach, indem Sie die Zeile suchen, die den Freiheitsgraden für die t-Statistik (n – 1) entspricht. Suchen Sie in dieser Zeile zwei Werte, zwischen denen Ihre t-Statistik liegt. Anschließend gehen Sie in dieser Spalte nach oben und lesen die Wahrscheinlichkeiten ab. Die Wahrscheinlichkeit, dass t außerhalb Ihres x-Werts liegt (die rechtsseitige Wahrscheinlichkeit), liegt irgendwo zwischen diesen beiden Wahrscheinlichkeiten. Beachten Sie, dass in der letzten Zeile der t-Tabelle df = ∞ steht, was die Werte für die z-Verteilung darstellt, weil t und z für große Stichprobengrößen sehr ähnlich sind.
: t- Verteilung,
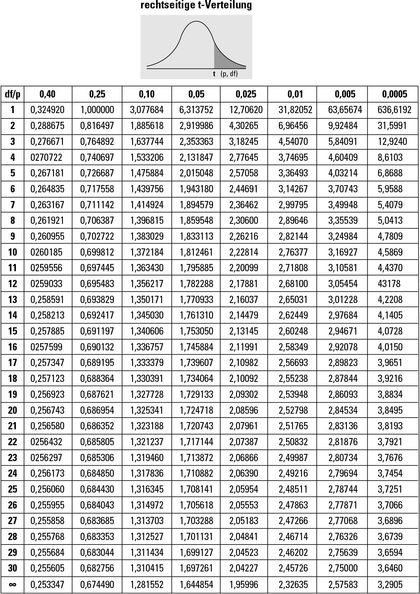
zeigt die Wahrscheinlichkeiten für die Binomialverteilung (siehe Kapitel 17). Um nutzen zu können, benötigen Sie drei Informationen aus der Aufgabenstellung, die Sie bearbeiten:
Die Stichprobengröße n Die Erfolgswahrscheinlichkeit p Den Wert von x, für den Sie die kumulative Wahrscheinlichkeit bestimmen wollenBestimmen Sie den Teil von , der für Ihr n vorgesehen ist, und lesen Sie in der Zeile für Ihr x und in der Spalte für Ihr p nach. Lesen Sie am Schnittpunkt dieser Zeile und Spalte die Wahrscheinlichkeit für x ab. Um die Wahrscheinlichkeit zu erhalten, kleiner, größer, größer oder gleich oder zwischen zwei Werten von x zu liegen, summieren Sie die entsprechenden Werte aus unter Verwendung der in Kapitel 16 beschriebenen Schritte.
: Die Binomialtabelle
Zahlen in der Tabelle stellen die Wahrscheinlichkeiten für Werte von x von 0 bis n dar.
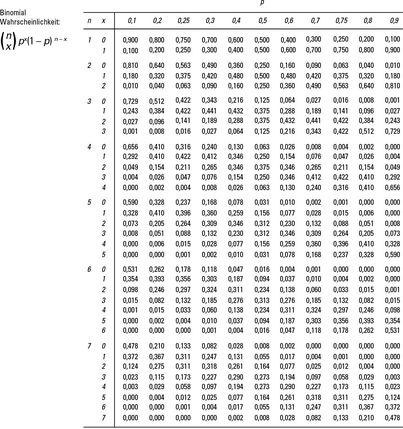
zeigt die rechtsseitigen Wahrscheinlichkeiten für die Chi-Quadrat-Verteilung (weitere Informationen über den Chi-Quadrat-Test finden Sie in Kapitel 14). Um nutzen zu können, benötigen Sie drei Informationen aus der Aufgabenstellung, die Sie bearbeiten:
Die Stichprobengröße n Den Wert von χ-Quadrat, für den Sie die rechtsseitige Wahrscheinlichkeit benötigen
: Chi-Quadrat-Tabelle
Wenn Sie mit einer Kreuztabelle arbeiten, benötigen Sie r = Anzahl der Zeilen und c = Anzahl der Spalten. Wenn Sie mit einem Test auf Güte der Anpassung arbeiten, benötigen Sie k - 1, wobei k die Anzahl der Kategorien ist.Die Freiheitsgrade für die Chi-Quadrat-Teststatistik sind (r - 1) * (c - 1), wenn Sie auf eine Assoziation zwischen zwei Variablen testen, wobei r und c die Anzahl der Zeilen bzw. Spalten in der Kreuztabelle sind. Bei einem Test auf Güte der Anpassung sind die Freiheitsgrade k - 1, wobei k die Anzahl der Kategorien darstellt (siehe Kapitel 15).
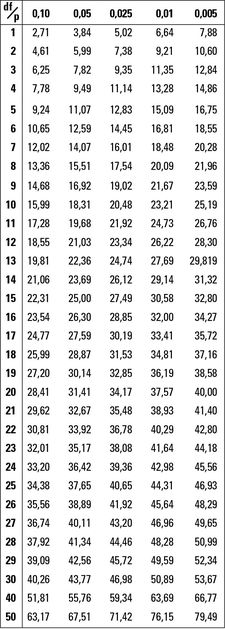
Suchen Sie in der Zeile für Ihre Freiheitsgrade den Wert, der Ihrer Chi-Quadrat-Teststatistik am nächsten kommt. Der Wert in der Spaltenüberschrift ist der Bereich rechts von der betreffenden Chi-Quadrat-Statistik (der über diese hinausgeht).
zeigt die kritischen Werte für den Rangsummentest, wobei α = 0,05 für zweiseitige Tests verwendet wird (das entspricht 0,025 für einseitige Tests). Weitere Informationen zu diesem Test finden Sie in Kapitel 18. Um nutzen zu können, benötigen Sie zwei Informationen über die Aufgabenstellung, die Sie bearbeiten:
Die Rangsummenstatistik T Die Stichprobengrößen der beiden Stichproben, n1 und n2Um den kritischen Wert für Ihre Rangsummenstatistik in zu finden, gehen Sie in die Spalte für n1 und die Zeile für n2. Am Schnittpunkt dieser Zeile und Spalte finden Sie den oberen und unteren kritischen Wert (TL und Tu) für den Rangsummentest.
Tabelle A 4: Rangsummentest
: Rangsummentabelle
zeigt die kritischen Werte für die F-Verteilung, wobei α gleich 0,05 ist. (Kritische Werte sind die Werte, die die Grenze zwischen dem Ablehnen von Ho und dem Beibehalten von Ho darstellen, siehe Kapitel 9.) Um nutzen zu können, benötigen Sie drei Informationen über die Aufgabenstellung, die Sie bearbeiten:
Die Stichprobengröße n Die Anzahl der Populationen (oder der zu vergleichenden Behandlungen), k Den Wert von F, für den Sie die kumulative Wahrscheinlichkeit benötigenUm in den kritischen Wert für Ihre F-Teststatistik zu finden, gehen Sie in die Spalte für die benötigten Freiheitsgrade (k – 1, n – k). Schneiden Sie die Spalte der Freiheitsgrade (k – 1) mit der Zeile der Freiheitsgrade (n – k), um den kritischen Wert auf der F-Verteilung zu finden. Weitere Informationen über den F-Test finden Sie in Kapitel 9.
: F-Tabelle
Diese Tabelle hilft Ihnen, zu vergleichen, zu unterscheiden und zu entscheiden, welche Analyse Sie wann verwenden sollten. Nutzen Sie sie als einfache Referenz oder zur Wiederholung für Prüfungen.
Diese Seite erklärt den Aufbau der Computerausgabe für die Mehrfachregression und ANOVA. Lehrer legen in Prüfungen gerne Computerausgaben vor und fordern Sie auf, diese zu interpretieren. Manchmal lassen sie auch Stellen frei und bitten Sie, diese anhand der vorliegenden Informationen auszufüllen – seien Sie also bereit! (Hinweis: Weitere Informationen darüber, wie die Computerausgaben in die Themenbereiche dieses Buches eingebunden sind, finden Sie in der Einführung sowie in Kapitel 1.)
[Zeile 1] = Dies ist das Modell für die Abschätzung von y anhand von x1 und x2 (Ebenengleichung).
[Zeile 2] = Der Koeffizient von x1 ist 0,007; die t-Statistik für das Testen seiner Signifikanz (vorausgesetzt, x2 ist im Modell enthalten) ist 2,16, was signifikant ist (p-Wert = 0,04, was kleiner als 0,05 ist).
[Zeile 3] = Der Koeffizient von x2 ist 0,026; die t-Statistik für das Testen seiner Signifikanz (vorausgesetzt, x1 ist im Modell enthalten) ist 2,22, was signifikant ist (p-Wert = 0,035, was kleiner als 0,05 ist).
[4] = Variabilität von y in Hinblick auf die vorhergesagten Werte (ein kleiner Wert ist gut).
[5] = Prozentsatz der Variabilität in y, der durch x1 und x2 erklärt wird (ein höherer Prozentsatz ist gut).
[6] = [5] korrigiert für die Anzahl der Variablen im Modell (hoch ist gut).
[Zeile 1] = Behandlung = Gruppe; k = 3 Gruppen, weil df = k - 1 = 2; SST = 20,58; MST = SST/df = 20,58/2 = 10,29. F = MST/MSE = 1,13 ist nicht signifikant (p-Wert = 0,329 > 0,05). (MSE siehe Zeile 2.) Es gibt also keinen Unterschied zwischen den Gruppen in Hinblick auf die y-Variable.
[Zeile 2] = df = n - k = 63, also ist n = 66 (aufgrund von k = 3 aus Zeile 1). MSE = SSE/df = 572,45/63 = 9,09. MSE ist der Nenner des F-Tests in Zeile 1.
[Zeile 3] = Bekannt ist: df Gesamt = n – 1, deshalb ist n = 66. Beachten Sie, dass SSTO = SST + SSE ist.
[Zeile 4] = Siehe [4], [5] und [6] aus der Regressions-Ausgabe. Sie erkennen, dass die Unterscheidung der Gruppen y nicht beeinflusst, weil R2 so klein ist – und das für die Anzahl der Gruppen korrigierte R2 noch kleiner.