CONTENTS

PREFACE

1: INTRODUCTION

1.1 HISTORICAL BACKGROUND

1.2 FUNDAMENTAL CONCEPTS OF LUMPED CIRCUITS

1.3 OUTLINE OF THE BOOK

1.4 “LOOP” INDUCTANCE VS. “PARTIAL” INDUCTANCE

2: MAGNETIC FIELDS OF DC CURRENTS (STEADY FLOW OF CHARGE)

2.1 MAGNETIC FIELD VECTORS AND PROPERTIES OF MATERIALS

2.2 GAUSS’S LAW FOR THE MAGNETIC FIELD AND THE SURFACE INTEGRAL

2.3 THE BIOT-SAVART LAW

2.4 AMPÈRE’S LAW AND THE LINE INTEGRAL

2.5 VECTOR MAGNETIC POTENTIAL

2.6 DETERMINING THE INDUCTANCE OF A CURRENT LOOP: A PRELIMINARY DISCUSSION

2.7 ENERGY STORED IN THE MAGNETIC FIELD

2.8 THE METHOD OF IMAGES

2.9 STEADY (DC) CURRENTS MUST FORM CLOSED LOOPS

3: FIELDS OF TIME-VARYING CURRENTS (ACCELERATED CHARGE)

3.1 FARADAY’S FUNDAMENTAL LAW OF INDUCTION

3.2 AMPERE’S LAW AND DISPLACEMENT CURRENT

3.3 WAVES, WAVELENGTH, TIME DELAY, AND ELECTRICAL DIMENSIONS

3.4 HOW CAN RESULTS DERIVED USING STATIC (DC) VOLTAGES AND CURRENTS BE USED IN PROBLEMS WHERE THE VOLTAGES AND CURRENTS ARE VARYING WITH TIME?

3.5 VECTOR MAGNETIC POTENTIAL FOR TIME-VARYING CURRENTS

3.6 CONSERVATION OF ENERGY AND POYNTING’S THEOREM

3.7 INDUCTANCE OF A CONDUCTING LOOP

4: THE CONCEPT OF “LOOP” INDUCTANCE

4.1 SELF INDUCTANCE OF A CURRENT LOOP FROM FARADAY’S LAW OF INDUCTION

4.2 THE CONCEPT OF FLUX LINKAGES FOR MULTITURN LOOPS

4.3 LOOP INDUCTANCE USING THE VECTOR MAGNETIC POTENTIAL

4.4 NEUMANN INTEGRAL FOR SELF AND MUTUAL INDUCTANCES BETWEEN CURRENT LOOPS

4.5 INTERNAL INDUCTANCE VS. EXTERNAL INDUCTANCE

4.6 USE OF FILAMENTARY CURRENTS AND CURRENT REDISTRIBUTION DUE TO THE PROXIMITY EFFECT

4.7 ENERGY STORAGE METHOD FOR COMPUTING LOOP INDUCTANCE

4.8 LOOP INDUCTANCE MATRIX FOR COUPLED CURRENT LOOPS

4.9 LOOP INDUCTANCES OF PRINTED CIRCUIT BOARD LANDS

4.10 SUMMARY OF METHODS FOR COMPUTING LOOP INDUCTANCE

5: THE CONCEPT OF “PARTIAL” INDUCTANCE

5.1 GENERAL MEANING OF PARTIAL INDUCTANCE

5.2 PHYSICAL MEANING OF PARTIAL INDUCTANCE

5.3 SELF PARTIAL INDUCTANCE OF WIRES

5.4 MUTUAL PARTIAL INDUCTANCE BETWEEN PARALLEL WIRES

5.5 MUTUAL PARTIAL INDUCTANCE BETWEEN PARALLEL WIRES THAT ARE OFFSET

5.6 MUTUAL PARTIAL INDUCTANCE BETWEEN WIRES AT AN ANGLE TO EACH OTHER

5.7 NUMERICAL VALUES OF PARTIAL INDUCTANCES AND SIGNIFICANCE OF INTERNAL INDUCTANCE

5.8 CONSTRUCTING LUMPED EQUIVALENT CIRCUITS WITH PARTIAL INDUCTANCES

6: PARTIAL INDUCTANCES OF CONDUCTORS OF RECTANGULAR CROSS SECTION

6.1 FORMULATION FOR THE COMPUTATION OF THE PARTIAL INDUCTANCES OF PCB LANDS

6.2 SELF PARTIAL INDUCTANCE OF PCB LANDS

6.3 MUTUAL PARTIAL INDUCTANCE BETWEEN PCB LANDS

6.4 CONCEPT OF GEOMETRIC MEAN DISTANCE

6.5 COMPUTING THE HIGH-FREQUENCY PARTIAL INDUCTANCES OF LANDS AND NUMERICAL METHODS

7: “LOOP” INDUCTANCE VS. “PARTIAL” INDUCTANCE

7.1 LOOP INDUCTANCE VS. PARTIAL INDUCTANCE: INTENTIONAL INDUCTORS VS. NONINTENTIONAL INDUCTORS

7.2 TO COMPUTE “LOOP” INDUCTANCE, THE “RETURN PATH” FOR THE CURRENT MUST BE DETERMINED

7.3 GENERALLY, THERE IS NO UNIQUE RETURN PATH FOR ALL FREQUENCIES, THEREBY COMPLICATING THE CALCULATION OF A “LOOP” INDUCTANCE

7.4 COMPUTING THE “GROUND BOUNCE” AND “POWER RAIL COLLAPSE” OF A DIGITAL POWER DISTRIBUTION SYSTEM USING “LOOP” INDUCTANCES

7.5 WHERE SHOULD THE “LOOP” INDUCTANCE OF THE CLOSED CURRENT PATH BE PLACED WHEN DEVELOPING A LUMPED-CIRCUIT MODEL OF A SIGNAL OR POWER DELIVERY PATH?

7.6 HOW CAN A LUMPED-CIRCUIT MODEL OF A COMPLICATED SYSTEM OF A LARGE NUMBER OF TIGHTLY COUPLED CURRENT LOOPS BE CONSTRUCTED USING “LOOP” INDUCTANCE?

7.7 MODELING VIAS ON PCBS

7.8 MODELING PINS IN CONNECTORS

7.9 NET SELF INDUCTANCE OF WIRES IN PARALLEL AND IN SERIES

7.10 COMPUTATION OF LOOP INDUCTANCES FOR VARIOUS LOOP SHAPES

7.11 FINAL EXAMPLE: USE OF LOOP AND PARTIAL INDUCTANCE TO SOLVE A PROBLEM

APPENDIX: FUNDAMENTAL CONCEPTS OF VECTORS

A.1 VECTORS AND COORDINATE SYSTEMS

A.2 LINE INTEGRAL

A.3 SURFACE INTEGRAL

A.4 DIVERGENCE

A.5 CURL

A.6 GRADIENT OF A SCALAR FIELD

A.7 IMPORTANT VECTOR IDENTITIES

A.8 CYLINDRICAL COORDINATE SYSTEM

A.9 SPHERICAL COORDINATE SYSTEM

TABLE OF IDENTITIES, DERIVATIVES, AND INTEGRALS USED IN THIS BOOK

REFERENCES AND FURTHER READINGS

INDEX

Copyright © 2010 by John Wiley & Sons, Inc. All rights reserved.

Published by John Wiley & Sons, Inc., Hoboken, New Jersey.

Published simultaneously in Canada.

No part of this publication may be reproduced, stored in a retrieval system, or transmitted in any form or by any means, electronic, mechanical, photocopying, recording, scanning, or otherwise, except as permitted under Section 107 or 108 of the 1976 United States Copyright Act, without either the prior written permission of the Publisher, or authorization through payment of the appropriate per-copy fee to the Copyright Clearance Center, Inc., 222 Rosewood Drive, Danvers, MA 01923, (978) 750-8400, fax (978) 750-4470, or on the web at www.copyright.com. Requests to the Publisher for permission should be addressed to the Permissions Department, John Wiley & Sons, Inc., 111 River Street, Hoboken, NJ 07030, (201) 748-6011, fax (201) 748-6008, or online at http://www.wiley.com/go/permission.

Limit of Liability/Disclaimer of Warranty: While the publisher and author have used their best efforts in preparing this book, they make no representations or warranties with respect to the accuracy or completeness of the contents of this book and specifically disclaim any implied warranties of merchantability or fitness for a particular purpose. No warranty may be created or extended by sales representatives or written sales materials. The advice and strategies contained herein may not be suitable for your situation. You should consult with a professional where appropriate. Neither the publisher nor author shall be liable for any loss of profit or any other commercial damages, including but not limited to special, incidental, consequential, or other damages.

For general information on our other products and services or for technical support, please contact our Customer Care Department within the United States at (800) 762-2974, outside the United States at (317) 572-3993 or fax (317) 572-4002.

Wiley also publishes its books in a variety of electronic formats. Some content that appears in print may not be available in electronic formats. For more information about Wiley products, visit our web site at www.wiley.com.

Library of Congress Cataloging-in-Publication Data:

Paul, Clayton R.

Inductance: loop and partial/Clayton R. Paul.

p. cm.

Includes bibliographical references and index.

ISBN 978-0-470-46188-4

1. Inductance. 2. Induction coils. I. Title. QC638.P38 2010

621.37’42-dc22

2009031434

This book is dedicated to the memory of my Father and my Mother

Oscar Paul

and

Louise Paul

PREFACE

This book has been written to provide a thorough and complete discussion of virtually all aspects of inductance: both “loop” and “partial.” There is considerable misunderstanding and misapplication of the important concepts of inductance. Undergraduate electrical engineering curricula generally discuss “loop” inductance only very briefly and only in one undergraduate course at the beginning of the junior year in a four-year curriculum. However, that curriculum is replete with the analysis of electric circuits containing the inductance symbol. In all those electric circuit analysis courses, the values of the inductors are given and are not derived from physical principles. Yet in the world of industry, the analyst must somehow obtain these values as well as construct inductors having the chosen values of inductance used in the circuit analysis. This book addresses that missing link: calculation of the values of the various physical constructions of inductors, both intentional and unintentional, from basic electromagnetic principles and laws.

In addition, today’s high-speed digital systems as well as high-frequency analog systems are using increasingly higher spectral content signals. Numerous “unintended” inductances such as those of the interconnection leads are becoming increasingly important in determining whether these high-speed, high-frequency systems will function properly. This is generally classified as the “signal integrity” of those systems and is an increasingly important aspect of digital system design as clock and data speeds increase at a dramatic rate. Some ten years ago the effects of interconnects such as printed circuit board lands on the function of the modules that lands interconnect were not important and could be ignored. Today, it is critical that circuit models of these interconnects be included in any analysis of the overall system. The concept of “partial inductance” is the critical link in being able to model these interconnects. Partial inductance is not covered in any undergraduate electrical engineering course but is becoming increasingly important in digital system design. A substantial portion of this book is devoted to that topic.

One of the important contributions of this book is the detailed derivation of the loop and partial inductances of numerous configurations of currentcarrying conductors. Although the derivations are sometimes tedious, there is nothing we can do about it because the results are dictated by the laws of electromagnetics, and these can be complicated. Unlike other textbooks, all the details regarding derivations for the inductance of inductors are given. Although these are simplified where possible, only so much simplification can be accepted if the reader is to have a clear and unambiguous view of how the result is obtained.

In Chapter 1 we discuss inductance and show important parallels between inductance and capacitance along with some historical details. All of the derivations of the inductance of various inductors first require that we obtain their magnetic fields. Chapter 2 is devoted to this task. The fundamental laws of Biot-Savart, Gauss, and Ampere are discussed, and numerous calculations of the magnetic fields are obtained from them. In addition, the vector magnetic potential method of computing the magnetic fields is also discussed, along with the method of images and energy stored in the magnetic field. In Chapter 3 we provide a complete explanation of how the inductance, which is computed for dc currents, can be used to characterize the effect of time-varying currents. Maxwell’s equations for time-varying currents are discussed in detail. An iterative solution of them is given which shows why and when the inductor, derived for dc currents, can be used to characterize the effects of time-varying currents.

All aspects of the derivation of the “loop” inductance of various currentcarrying loops are covered in Chapter 4. The flux linkage method, the vector magnetic potential method, and the Neumann integral for determining the “loop” inductance are used, and the “loop” inductances are calculated from all three methods. The proximity effect for closely spaced conductors is discussed along with the loop inductance of various transmission lines.

In Chapter 5 we provide details for computation of the “partial” inductances of wires. Both the self-partial inductance of wires and the mutual partial inductances between wires are derived. These generic results can then be used to “build” a model for other current-carrying structures. Chapter 6 contains all corresponding details about the derivation of the partial inductances of conductors of rectangular cross section, referred to as “lands.” The concept of geometric mean distance as an aid to the calculation of partial inductances is discussed and derived for various structures.

The final chapter of the book, Chapter 7, provides a focus on when one should use “loop” inductance and when one should use “partial” inductance for determining the effect of current-carrying conductors. This chapter is meant to provide a simple discussion of this in order to focus the results of previous chapters. The chapter concludes with the solution of a problem involving coupling between two circuit loops using the “loop” inductance method and then using the “partial” inductance method. Both methods yield the same answer, as expected. This example clearly shows the advantages of using “partial” inductance to characterize “unintentional inductors” such as wires and lands.

With the present and increasing emphasis on high-speed digital systems and high-frequency analog systems, it is imperative that system designers develop an intimate understanding of the concepts and methods in this book. No longer can we rely on low-speed, low-frequency systems to keep us from needing to learn these new concepts and analysis skills.

The author would like to acknowledge Dr. Albert E. Ruehli of the IBM T.J. Watson Research Center for many helpful discussions of partial inductance over the years.

CLAYTON R. PAUL

Macon, Georgia

1

INTRODUCTION

The concept of inductance is simple and straightforward. However, actual computation of the inductance of various physical structures and its implementation in an electric circuit model of that structure is often fraught with misconceptions and mistakes that prevent its correct calculation and use. This book is intended to ensure the correct understanding, calculation, and implementation of inductance.

1.1 HISTORICAL BACKGROUND

Knowledge of magnetism has a long history [3]. A type of iron ore called lodestone had been discovered in Magnesia in Asia. This material had some interesting properties of magnetic attraction at a distance of other ferromagnetic substances and was known to Plato and Socrates. In the sixteenth century, William Gilbert first postulated that Earth was a giant spherical magnet, and A. Kirchner, in the seventeenth century, demonstrated that the two poles of a magnet have equal strength. Pierre de Marricourt constructed a compass in 1629 that allowed the determination of the direction of the North Pole of the Earth. In 1750, John Mitchell determined the universal principle that force at a distance depends on the inverse square of the distance. At the beginning of the nineteenth century, Alessandro Volta developed a battery (called a pile). This allowed the production of a current in a conducting material such as a wire. In 1820, Hans Christian Oersted showed that a current in a wire caused the needle of a compass to deflect. Around the same time, Andre Ampere conducted a set of experiments, resulting in his famous law. At about the same time, Jean-Baptiste Biot and Felix Savart formulated their important law governing the magnetic fields produced by currents: the Biot-Savart law. So up to this time it was known that in addition to permanent magnets, a current would produce a magnetic field. In 1831, Michael Faraday discovered that a time-changing magnetic field would also produce a current in a closed loop of wire. This discovery formed the essential idea of the inductance of a current loop. James Clerk Maxwell unified all this knowledge of the magnetic field as well as the knowledge of the electric field in 1873 in his renowned set of equations.

Extensive work on the calculation of the magnetic field of various current distributions and the associated concept of inductance dates back to the late nineteenth and early twentieth centuries. In fact, Maxwell in his famous treatise discussed inductance in 1873 [23]. An enormous amount of work was published on the determination of inductance from 1900 to 1920. (See the extensive list of references on magnetic fields in the book by Weber [11] and on inductance in the book by Grover [14].) This early work on inductance at the turn of the century was spurred by the introduction of 60-Hz ac power and its generation, distribution, and use. Some books, particularly those of the early twentieth century, tended to give only formulas for the magnetic fields of various distributions of currents and their inductance with little or no detail about the derivation of formulas. In that era, computers did not exist, so that many of the books and papers simply gave tables of values for the magnetic field and inductance as a function of certain parameters. Another important purpose of this book is to show, in considerable detail, how the results for the magnetic fields and the inductance are derived. All details of each derivation are shown. At the end of the book is a list of significant references and further readings on the subject of the computation of magnetic fields and inductance of various current-carrying structures. References to these are denoted in brackets.

1.2 FUNDAMENTAL CONCEPTS OF LUMPED CIRCUITS

We construct lumped-circuit models of electrical structures using the concepts and models of resistance, capacitance, and inductance [1,2]. We then solve for the resulting voltages and currents of that particular interconnection of circuit elements using Kirchhoff’s voltage law (KVL) (which relates the various voltages of the particular interconnection of circuit elements), Kirchhoff’s current law (KCL) (which relates the various currents of the particular interconnection of circuit elements), and the laws of the circuit elements (which relate the voltages of each circuit element to its currents) [1,2]. It is important to keep in mind that these lumped-circuit models are valid only if the largest physical dimension of the circuit is “electrically short” (e.g., < ^λ/10), where a wavelength λ is defined as the ratio of the velocity of wave propagation (along the component attachment leads), v, and the frequency of the wave, f [3–6]:

(1.1)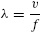

If the medium in which the circuit is immersed and through which the waves propagate along the connection leads is free space (essentially, air), the velocity of propagation of those waves is the speed of light, which is approximately v₀ ≅ 3 × 10⁸ m/s. For a printed circuit board (PCB), the velocity of propagation of the waves traveling along the lands on that board is about 60% of that of free space, due to the interaction of the fields with the board substrate, and the wavelengths are consequently shorter than in free space. Hence, circuit dimensions on a PCB are electrically longer than in free space. For a sinusoidal wave in free space at a frequency of 300 MHz, a wavelength is 1 m. At frequencies below this, the wavelength is proportionately larger than 1 m, and for frequencies above this, the wavelength is proportionately smaller. For example, at a frequency of 3 MHz a wavelength in free space is 100 m, and at a frequency of 3 GHz a wavelength in free space is 10 cm. Hence, for lumped-circuit concepts to be valid for a circuit having a sinusoidal source of frequency 3 MHz, the maximum physical dimension of the circuit must be less than about 10 m or about 30 ft. Similarly, for a circuit having a sinusoidal source of frequency 3 GHz, the maximum physical dimension must be less than about 1 cm or about 0.4 inch for it to be modeled as a lumped circuit. Today’s digital electronics have clock and data rates on the order of 300 MHz to 3 GHz. But these digital waveforms have a spectral content consisting of harmonics (integer multiples) of the basic repetition rate, which are generally significant up to at least the fifth harmonic. Hence, a 300-MHz clock rate has spectral content up to at least 1.5 GHz, and a 3-GHz clock rate has spectral content up to at least 15 GHz! So the lumped-circuit models (and their constituent components of capacitance and inductance) that were so reliable some 10 years ago are becoming less valid today. This trend will no doubt continue in the future as the requirement for higher clock and data speeds continues to increase, and the reader should keep in mind this fundamental limitation of inductance, capacitance, and the lumped-circuit models that use these elements.

The laws governing the calculation of resistance, capacitance, and inductance are written in terms of the vectors of the five basic electromagnetic field vectors, which are summarized in Table 1.1. Therefore, if we are to correctly calculate and understand the ideas of capacitance and inductance of a physical structure as well as use them correctly to construct a lumped-circuit model of that structure, we must understand some elementary properties of vectors and some basic vector calculus concepts. Trying to circumvent the use of vector calculus ideas by relying on one’s life experiences to compute and interpret the meaning of the capacitance and inductance of a structure properly has caused many of the incorrect results and misunderstanding, as well as the numerous erroneous applications that are seen throughout the literature and in conversations with engineering professionals. References [3–6] give extensive details on vector algebra and vector calculus. The Appendix of this book contains a review of the vector algebra and vector calculus concepts that are required to understand and compute the inductance of all physical structures.

TABLE 1.1. Electromagnetic Field Vectors

Symbol	Vector	Units
J	Current density	A/m2
	Electric field vectors
E	Electric field intensity	V/meter
D	Electric flux density	C/m2
	Magnetic field vectors
H	Magnetic field intensity	A/meter
B	Magnetic flux density	Wb/m2 = T

The lumped-circuit elements of resistance, capacitance, and inductance are derived fundamentally for static conditions. Capacitance is derived for conductors that are supporting charges whose positions on those conductors are fixed. Resistance as well as inductance are derived for currents that are not varying with time: that is, direct (dc) currents. For charge distributions and currents that do not vary with time, the electromagnetic field equations (Maxwell’s equations) that govern the field vectors simplify considerably. However, the resulting electrical elements of resistance, capacitance, and inductance can be used to construct lumped-circuit models of a structure whose currents and charge distributions vary with time. This is valid as long as the sources driving the circuit have frequency content such that the largest physical dimension of the circuit is electrically small (see Section 3.4).

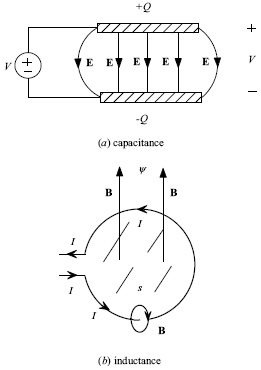
To understand the computation of inductance (the main subject of this book), it is useful to understand the dual concept of capacitance and its calculation. The basic idea of the capacitance of a two-conductor structure is summarized in Fig. 1.1(a). If we apply a dc voltage V between two conductors, a charge Q is transferred to and stored on those conductors (equal magnitude on both conductors, but opposite polarity). This charge induces an electric field intensity E between the two conductors that is directed from the conductor containing the positive charge to the conductor containing the negative charge. Alternatively, we could look at this process in a different way. Place a charge on the two conductors (equal magnitude on both conductors but opposite polarity). This charge will result in an electric field E between the two conductors which when integrated with a line integral (see the Appendix) gives the resulting voltage between the two conductors:

(1.2)

where the path for integration is from a point on the negatively charged conductor to a point on the positively charged conductor [3–6]. In either case, the capacitance of the structure is the ratio of the charge stored on the two conductors and the voltage between them [1–6]:

(1.3)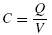

Hence, the capacitance of a structure represents the ability of that structure to store charge. However, the capacitance of the structure is independent of the values of the voltage V and the charge Q and depends only on their ratio. Hence, the capacitance C of a structure depends only on its dimensions, its shape, and the properties of the medium surrounding the conductors (e.g., free space, Teflon). There is energy stored in the electric field in the space around the two conductors. That stored energy is [3–6]

(1.4)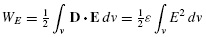

where v is the volume of the entire space surrounding the conductors, ε is the permittivity of the surrounding medium, and we have used the relation D = εE. In terms of capacitance this stored energy is [1,2]

(1.5)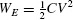

The dual concept is that of inductance, illustrated in Fig. 1.1(b). If we pass a steady (dc) current I around a conducting loop of wire, the current will produce a magnetic flux density B that circulates about the wire with its direction about the wire determined by the right-hand rule: If we place the thumb of the right hand in the direction of the current, the fingers will show the direction of the resulting magnetic field that is circumferential about the current. This causes a magnetic field B to penetrate the surface that is enclosed by the loop of current. The total magnetic flux penetrating the surface enclosed by the current loop is obtained with a surface integral (see the Appendix) as [3-6],

(1.6)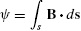

where s is the surface of the loop that is surrounded by the current. The inductance of the loop is the ratio of the total magnetic flux penetrating the loop and the current that produced it [1–6]:

(1.7)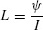

If the surrounding medium is not ferromagnetic (iron is an example of a ferromagnetic material), that is, is not magnetizeable, the inductance is independent of the values of the flux and the current and depends only on the dimension of the loop, its shape, and the properties of the medium surrounding the conductor (e.g., free space). There is energy stored in the magnetic field in the space around the conductor loop. That stored energy is [3–6]

(1.8)

where v is the volume of the entire space surrounding the conductors, μ is the permeability of the surrounding medium, and we have used the relation B = μH. In terms of inductance, the stored energy is [1,2]

(1.9)

The duality between the concept of capacitance and the corresponding concept of inductance is striking. However, the methods and techniques for computing them are generally different in both concept and method. Visualizing how to go about calculating the capacitance of a particular structure is usually much easier to understand than is the visualization of how to go about calculating inductance.

1.3 OUTLINE OF THE BOOK

In Chapter 2 we summarize the fundamental electromagnetic field laws governing the magnetic field, those of Gauss, Ampére, and Biot-Savart, on which the inductance calculation is based. The magnetic fields B of various configurations carrying a dc current are derived from these laws. This is a necessary first step in computing the inductance of a structure since the magnetic flux ψ penetrating the surface that comprises the inductance must be computed from B via (1.6). The inductance of the structure is then obtained as the ratio of the flux and the current producing it via (1.7). The derivation of the B field for a particular structure that carries a dc current generally involves the setting up and evaluation of somewhat complicated integrals. An extensive table of integrals is given by Dwight [7]. Furthermore, the next step in calculation of the inductance of a structure requires a further integration of B as in (1.6). An alternative way of computing the B field of a current-carrying structure is obtained using the vector magnetic potential A. In some cases it is easier to compute A directly and from this obtain B by differentiation. The method of images for simplifying problems involving currents over large “ground planes” is also discussed. The commonly assumed fact that all dc currents must “return to their source” and therefore must comprise closed loops is proven.

The important ideas that arise when the currents are, instead of dc, varying with time are discussed in Chapter 3. The fundamental law that provides an understanding of how an inductance produces a voltage between its two terminals is Faraday’s law of induction, which is examined in detail. The important notion of displacement current in Ampere’s law, which affords an understanding of how a capacitance can conduct a time-varying current through it, is also discussed. The important concepts of waves, wavelength, time delay, and electrical dimensions that allow these static ideas of capacitance and inductance to be incorporated into lumped circuits which have time-varying sources driving them are examined. The important ability of being able to use a quantity that is derived for static (dc) currents (e.g., inductance and capacitance) in a circuit where the currents vary with time is shown in terms of an iterative expansion of the electromagnetic fields. Finally, conservation of energy in the electromagnetic field and Poynting’s theorem are reviewed.

With this requisite background, we are able to understand how to calculate and interpret the meaning of the “loop inductance” of a closed loop of current, which is given in Chapter 4. The “loop inductances” for various structures are also derived in Chapter 4 using several methods.

The remaining chapters are devoted to the concept of “partial inductance,” which is rapidly becoming important in today’s high-speed digital electronics. The general concept of “partial inductance” is examined in Chapter 5, and the self and mutual partial inductances of straight wire segments are determined. The self and mutual partial inductances of conductors of rectangular cross section, which the “lands” on printed circuit boards (PCBs) represent, are determined in Chapter 6. Chapter 7 is devoted to a critical examination of the relative merits of using loop inductances to characterize current loops versus the use of partial inductances. A fairly complex structure is analyzed by first characterizing it with loop inductances and then characterizing it with partial inductances. This example is quite useful in bringing together all the concepts of the previous chapters and in comparing their relative merits and deficiencies.

1.4 “LOOP” INDUCTANCE VS. “PARTIAL” INDUCTANCE

It is critically important that the reader understand the following two distinctions with regard to inductance. In undergraduate electrical engineering courses, only the concept of the inductance of a complete loop of current is studied. (It is shown in Section 2.9 that dc currents must form closed loops.) This “loop inductance” is given in (1.7) and requires that we be able to compute the magnetic flux ψ that passes through the enclosed surface of a closed current loop, as illustrated in Fig. 1.1(b). Therefore, computation of the loop inductance of a structure requires that we be able to identify the complete current loop. For “intentional” inductors this current loop is rather obvious. For example, if we wind several turns of wire around a ferromagnetic toroid core, the loop area of the current that the magnetic flux passes through is evident. Hence, the concept of loop inductance of intentional inductors is useful in that it allows us to characterize those as lumped-circuit elements.

On the other hand, if we want to assign an “inductance” to segments of a conductor on a printed circuit board (referred to as lands), there are several problems in trying to use the concept of loop inductance to do so. The first problem is that we must be able to determine the complete current loop path in order to calculate loop inductance of that current loop. In other words, we must be able to identify not only the “going down” path from the source to the load (which is relatively easy to do) but also the “return current” path of the current back to the source in order to determine the complete current loop. In today’s densely packed integrated circuits and printed circuit boards carrying currents having ever-increasing spectral content, this has become virtually impossible to do! Furthermore, the complete path for the current depends on the frequency of the current. For one frequency, the return current will take a particular path, but for a higher frequency the path of the return current may be entirely different!

So the first problem with using loop inductance to model the conductors of a loop is that at different frequencies, the return path of the loop current may be different. This is best illustrated by the situation of a coaxial cable above a ground plane shown in Fig. 1.2. (See [5] for an analysis of this problem.) At dc and low frequencies, the current I takes its return path, I_G, through the massive ground plane. However, at higher frequencies, the current I takes its return path up through the shield, I_S. Therefore, the return paths and hence the complete current loops are different for different frequencies. So if we were to compute the loop inductance it would appear that we would have two different values, depending on the frequency of the current.

The final and most important problem in trying to use loop inductance to allocate inductances to the individual lands on a PCB is that the total loop inductance of a current loop cannot be placed in any unique position in that loop. For example, the current loop in Fig. 1.1(b) is said to present an inductance at its input terminals. But that is a loop inductance that cannot, a priori, be divided into portions that are associated with segments of that loop!

Figure 1.3 illustrates this problem of trying to use loop inductance to model the inductance of portions of the PCB lands. We have shown a CMOS inverter that is attached to a capacitive load (perhaps representing the input to another CMOS inverter). The +5-V output of the power supply is attached to the +5-V power pin of the CMOS module via a land on the PCB. Similarly, the ground terminal of the power supply is attached to the ground pin of the CMOS module with another land on the PCB. As the inverter switches from the LOW to HIGH state, the current, I_L-H, is drawn from the power supply through the +5-V land and through the inverter to charge the capacitor to put the load voltage, V_L, in the HIGH state and returns to the power supply through the ground land. When the inverter switches, the load capacitor then discharges via current I_H-L through the inverter via a different loop: from the capacitor, through the inverter, and back to the capacitor. We have shown the conductors as each having associated individual inductances. The land connecting the +5-V output of the power supply to the +5-V pin of the inverter is shown as having an inductance L_PR. The land connecting the ground of the power supply to the ground pin of the inverter and the land connecting the bottom of the capacitor to the ground pin of the inverter are also shown as having inductances L_GB. (Although these two inductances have the same symbol, they obviously have different values, due to the different lengths of these return paths.) The current I_L-H clearly forms a loop: from the power supply through the inverter, through the capacitor, and back to the power supply. When the inverter is switching from LOW to HIGH, the current I_L-H through the +5-V land increases in value in order to charge the capacitor. Hence, a voltage is developed across L_PR of

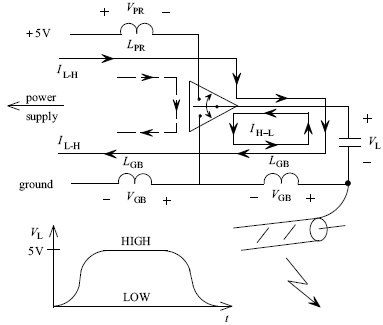
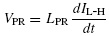
This is referred to as power rail collapse, since the voltage of the power pin of the inverter is 5 – V_PR, and hence the voltage of the +5-V pin of the inverter module drops in value from +5-V. Similarly, the voltage at the ground pin of the inverter goes from zero to V_GB:

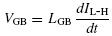
This is referred to as ground bounce. On the other hand, when the load voltage is transitioning from HIGH to LOW state, a voltage is developed across the V_GB of the other ground land as the current I_H-L from the capacitor discharges through the inverter and returns to the capacitor.

Although at first glance this seems to be a straightforward characterization of the individual lands with an inductance, it is not. What do we mean by the inductances of the two lands, L_PR and L_GB? These certainly are not loop inductances because the total inductance of a loop cannot be placed uniquely in any segment of the loop. In fact, these are “partial inductances.” But the type of diagram shown in Fig. 1.3 is seen throughout the literature. The problem here is that few people know how to compute L_PR and L_GB. Even worse, they often mistakenly compute L_PR and L_GB using a formula for a loop inductance they find in a handbook that does not apply to these inductances, thereby giving erroneous results for the magnitudes of V_PR and V_GB!

So loop inductance is not useful in modeling an “unintended inductance” to obtain the voltage developed between its two ends, due to a rate of change of current through it. However, using the concept of loop inductance to model “intended” physical inductors such as a toroid or a solenoid is a useful application of that concept. On the other hand, the concept of partial inductance allows us to represent the lands on a PCB as well as other types of conductors with inductances and to compute the values of those inductances uniquely to determine the correct voltage drop between two ends of the conductor. Unlike loop inductances, we can compute partial inductances without the necessity of having to be able to identify the return paths for the currents! We simply model all conductors with their partial inductances (self and mutual between this and other conductors in the circuit), build a lumped-circuit model using these partial inductances, and “turn the crank” (analyze the resulting lumpedcircuit model) to find the return paths for the currents rather than trying to guess their paths a priori. There is a dual concept to partial inductance that is referred to by the author as generalized capacitance (see references [5,8] for a discussion).

Prior to a decade ago, when the digital clock and data speeds and their spectral content were below about 100 MHz and the density of electronic circuits was not what it is today, the concept of partial inductance was not as important. Today, it is a virtual necessity if we are to cope with the rapidly escalating densities of electronic circuits whose conductors carry currents having increasingly higher spectral content.

The units of the quantities are named for the great scientists who made major contributions to the discovery of these phenomena. Throughout this book, we use the abbreviations A, Wb, H, and T, respectively, for the units amperes, webers, henrys, and tesla. The standard is to use lowercase for the first letter of each of the names of these units and capital letters in their abbreviations.