

Ian Stewart
Welt-Formeln
17 mathematische Gleichungen, die Geschichte machten
Aus dem Englischen von Monika Niehaus und Bernd Schuh
Rowohlt E-Book

Ian Stewart, geboren 1945, ist der beliebteste Mathematik-Professor Großbritanniens. Seit Jahrzehnten bemüht er sich erfolgreich, seine Wissenschaft zu popularisieren. Er studierte Mathematik in Cambridge und promovierte an der Universität Warwick. Dort ist er heute Professor für Mathematik und Direktor des Mathematics Awareness Center. Seit 2001 ist Stewart zudem Mitglied der Royal Society. Er lebt mit seiner Familie in Coventry. Er hat über 80 Bücher publiziert, bei rororo sind lieferbar: «Professor Stewarts mathematisches Sammelsurium» (62581) und «Professor Stewarts mathematische Schätze» (62690).
Sie haben die Geschichte des Menschen mindestens ebenso beeinflusst wie Kriege, Revolutionen und die Mächtigen der Welt – Gleichungen fassen in wenigen Symbolen den Fortschritt des Wissens zusammen. Vom Bau der Pyramiden bis zur Satellitennavigation bilden sie die Basis jeder Erfindung. Manche von ihnen sind gar zu Ikonen der Moderne geworden, zum Beispiel Einsteins E=mc². In diesem Buch erklärt uns Englands Mathe-Guru Ian Stewart die wichtigsten 17: ihre Vorgeschichte, ihren praktischen Nutzen, die Bedeutung der Zeichen. Vom Satz des Pythagoras über Logarithmen, imaginäre Zahlen, die Differentialrechnung, Newtons Gravitationsgesetz oder Gauss' Normalverteilung bis hin zum zweiten Hauptsatz der Thermodynamik oder zur Chaostheorie hat er Gleichungen ausgewählt, die jedem von uns in der einen oder anderen Form schon einmal begegnet sind.
Deutsche Erstausgabe
Veröffentlicht im Rowohlt Verlag, Reinbek bei Hamburg, März 2014
Copyright der deutschsprachigen Ausgabe
© 2014 by Rowohlt Verlag GmbH, Reinbek bei Hamburg
Dieses Werk ist urheberrechtlich geschützt, jede Verwertung bedarf der Genehmigung des Verlages
Die englische Originalausgabe erschien 2012 unter dem Titel
«Seventeen Equations that Changed the World» bei Profile Books, London.
Copyright © 2012 by Joat Enterprises
Redaktion Heiner Höfener
Umschlaggestaltung ZERO Werbeagentur, München
(Umschlagabbildung: FinePic, München)
Schrift DejaVu Copyright © 2003 by Bitstream, Inc. All Rights Reserved.
Bitstream Vera is a trademark of Bitstream, Inc.
ISBN Printausgabe 978-3-499-63029-3
ISBN E-Book 978-3-644-50681-7
www.rowohlt.de
ISBN 978-3-644-50681-7
The Penguin Book of Curious and Interesting Mathematics von David Wells zitiert eine Kurzform des Witzes: Ein Indianerhäuptling hatte drei Frauen, die bald gebären würden, die eine auf einer Büffelhaut, die andere auf einer Bärenhaut und die dritte auf einer Nilpferdhaut. Nach einiger Zeit schenkte ihm die erste einen Sohn, die zweite eine Tochter und die dritte Zwillinge, einen Jungen und ein Mädchen, was den wohlbekannten Satz illustriert, dass die Squaw auf dem Nilpferd gleich der Summe der Squaws auf den beiden anderen Häuten ist. Der Kalauer datiert mindestens auf die Mitte der 1950er Jahre zurück, als er in der BBC-Radioserie «My Word» ausgestrahlt wurde, die von den Comedy-Scriptwritern Frank Muir und Denis Norden moderiert wurde. (Anmerkung der Übersetzer: Der Wortwitz basiert auf der ähnlichen Aussprache einiger englischer Begriffe: hide [Haut] = side [Seite]; hippopotamus [Nilpferd] = hypotenuse [Hypotenuse], squaw [indianische Frau] = square [Quadrat].)
Zitiert ohne Referenz in: http://www-history.mcs.st-and.ac.uk/HistTopics/Babylonian_Pythagoras.html
A. Sachs, A. Goetze und O. Neugebauer. Mathematical Cuneiform Texts, American Oriental Society, New Haven 1945.
Die Abbildung ist aus Gründen der Bequemlichkeit in Abbildung 60 wiederholt.
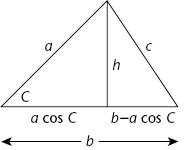
Abbildung 60: Ein Dreieck wird in zwei rechtwinklige Dreiecke geteilt.
Die senkrechte Teilung zerlegt die Seite b in zwei Stücke. Aus der Trigonometrie ergibt sich, dass ein Stück die Länge a cos C hat, das andere demnach die Länge b – a cos C. Sei h die Höhe der Senkrechten. Dann gilt nach Pythagoras

das heißt:

Zieht man die erste Gleichung von der zweiten ab, verschwindet das unerwünschte h2, ebenso heben sich die Terme a2 cos2 C weg, und es bleibt

was zur angegebenen Formel führt.
http://www.17centurymaths.com/contents/napiercontents.html
Zitiert aus einem Brief von John Marr an William Lilly.
Die Prosthaphäresis basierte auf einer trigonometrischen Formel, die von François Viète entdeckt wurde, nämlich
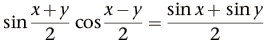
Wenn man eine Sinustabelle besaß, erlaubte einem die Formel, jedes Produkt allein mit Hilfe von Summen, Differenzen und Division durch 2 zu berechnen.
Keynes hat diese Vorlesung niemals gehalten. Die Royal Society wollte 1942 Isaac Newtons 300. Geburtstags gedenken, doch der Zweite Weltkrieg kam dazwischen, daher wurde die Feier auf 1946 verschoben. Die Redner waren die Physiker Edward da Costa Andrade und Niels Bohr sowie die Mathematiker Herbert Turnbull und Jacques Hadamard. Die Gesellschaft hatte auch Keynes eingeladen, der sich nicht nur für Ökonomie, sondern auch für Newtons Manuskripte interessierte. Er hatte einen Vortrag mit dem Titel «Newton, the man» verfasst, verstarb jedoch kurz vor dem Ereignis. Sein Bruder Geoffrey hielt den Vortrag an seiner Stelle.
Dieser Satz stammt aus einem Brief, den Newton 1676 an Hooke schrieb. Er war nicht neu: Im Jahr 1159 schrieb John von Salisbury: «Bernard von Chartres meinte öfter, dass wir wie Zwerge sind, die auf den Schultern von Riesen stehen, sodass wir mehr sehen können als sie.» Im 17. Jahrhundert war der Satz bereits zu einer stehenden Redewendung geworden.
Teilen durch null führt zu fehlerhaften Beweisen. So können wir beispielsweise «beweisen», dass alle Zahlen gleich null sind. Nehmen wir an, dass a = b ist. Daher ist a2 = ab, also a2 – b2 = ab – b2. Durch Faktorenzerlegung erhält man (a + b)(a – b) = b(a – b). Teilung durch (a – b) führt zu dem Schluss, dass a + b = b ist. Daher ist a = 0. Der Fehler liegt in der Division durch (a – b), was 0 ist, da wir angenommen haben, dass a = b ist.
Richard Westfall. Never at Rest, Cambridge University Press, Cambridge 1980, p. 425 (deutsch: Isaac Newton, Spektrum Akademischer Verlag, 1996).
Erik H. Hauri, Thomas Weinreich, Alberto E. Saal, Malcolm C. Rutherford und James A. Van Orman. High pre-eruptive water contents preserved in lunar melt inclusions, Science Online (26. Mai 2011) 1204626. [DOI:10.1126/science.1204626]. Ihre Ergebnisse wurden kontrovers diskutiert.
Das ist jedoch kein Zufall. Es funktioniert für jede stetig differenzierbare Funktion: eine Funktion mit einer stetigen Ableitung. Dazu gehören sämtliche Polynome und alle konvergenten Potenzreihen, wie die logarithmischen, die Exponential- und die verschiedenen trigonometrischen Funktionen.
Die moderne Definition lautet: Eine Funktion f(h) strebt einem Grenzwert L zu, wenn h null zustrebt, falls für jedes ε> 0 ein δ> 0 existiert, sodass für |h|< δ |f(h) – L|<ε gilt. Durch die Verwendung eines beliebigen ε> 0 vermeidet man, sich auf irgendetwas Fließendes oder kleiner Werdendes zu beziehen: Es berücksichtigt sämtliche möglichen Werte auf einen Streich.
Die Schöpfungsgeschichte spricht vom «Firmament». Dies bezieht sich nach Ansicht der meisten Gelehrten auf den alten hebräischen Glauben, dass die Sterne winzige Lichter sind, die an einem festen, wie eine Halbkugel geformten Himmelsgewölbe befestigt sind. So sieht der Nachthimmel aus: Die Art und Weise, wie unsere Augen auf ferne Objekte reagieren, lässt es so erscheinen, als hätten die Sterne alle etwa den gleichen Abstand von uns. Viele Kulturen, vor allem im Mittleren und Fernen Osten, stellten sich den Himmel als eine sich langsam drehende Schüssel vor.
Der Große Komet von 1577 ist nicht der Halley’sche Komet, sondern ein anderer Komet von historischer Bedeutung, der heute den Namen C/1577 V1 trägt. 1577 n. Chr. war er mit bloßem Auge zu sehen. Brahe beobachtete den Kometen und kam zu dem Schluss, dass sich Kometen außerhalb der Erdatmosphäre befinden. Gegenwärtig ist der Komet rund 24 Milliarden Kilometer von der Sonne entfernt.
Die Zahl wurde erst 1798 bestimmt, als Henry Cavendish in einem Laborexperiment einen einigermaßen präzisen Wert erzielte. Er liegt bei 6,67 × 10–11 Newton mal Meter zum Quadrat pro Kilogramm zum Quadrat.
June Barrow-Green. Poincaré and the Three Body Problem, American Mathematical Society, Providence 1997.
Im Jahr 1535 lieferten sich die beiden Mathematiker Antonio Fior und Niccolò Fontana (der den Spitznamen Tartaglia, der Stotterer, trug) einen öffentlichen Wettstreit. Sie legten einander kubische Gleichungen zur Lösung vor, und Tartaglia schlug Fior vernichtend. Damals wurden kubische Gleichungen in drei separate Typen eingeteilt, da negative Zahlen nicht anerkannt wurden. Fior wusste nur, wie man einen Typ löst; anfangs wusste Tartaglia, wie man einen anderen Typ löst, aber kurz vor dem Wettkampf fand er heraus, wie man auch die beiden anderen Typen löst. Dann gab er Fior nur die Typen vor, von denen er wusste, dass dieser sie nicht lösen konnte. Cardano, der an seinem Algebralehrbuch arbeitete, hörte von dem Wettkampf und erkannte, dass Fior und Tartaglia wussten, wie man kubische Gleichungen löst. Diese Entdeckung würde das Buch deutlich aufwerten, daher bat er Tartaglia, ihm seine Methode zu erklären.
Schließlich verriet ihm Tartaglia das Geheimnis und behauptete später, Cardano habe versprochen, es niemals öffentlich zu machen. Doch die Methode erschien in der Ars Magna, und so beschuldigte Tartaglia Cardano des Plagiats. Cardano hatte jedoch eine Entschuldigung und zudem einen guten Grund, sein Versprechen zu umgehen. Sein Schüler Lodovico Ferrari hatte herausgefunden, wie man biquadratische Gleichungen löst, eine ebenso neue und dramatische Entdeckung, und Cardano wollte sie ebenfalls in sein Buch aufnehmen. Ferraris Methode verlangte jedoch die Lösung einer damit verknüpften kubischen Gleichung, daher konnte Cardano Ferraris Entdeckung nicht publizieren, ohne gleichzeitig Tartaglias Lösung öffentlich zu machen.
Dann erfuhr er, dass Fior ein Schüler von Scipione del Ferro war, von dem es gerüchteweise hieß, er habe alle drei Typen kubischer Gleichungen gelöst und nur einen Typ an Fior weitergegeben. Del Ferros unveröffentlichte Schriften befanden sich im Besitz von Annibale della Nave. Daher reisten Cardano und Ferrari 1543 nach Bologna, um della Nave zu konsultieren, und in den Unterlagen fanden sie Lösungen für alle drei Typen kubischer Gleichungen. Daher konnte Cardano mit Fug und Recht behaupten, dass er del Ferros und nicht Tartaglias Methode veröffentlicht hatte. Dennoch fühlte sich Tartaglia betrogen und publizierte eine lange, bittere Schmährede gegen Cardano. Ferrari forderte ihn zu einer öffentlichen Debatte heraus und gewann sie mühelos. Danach konnte Tartaglia seine Reputation niemals mehr völlig wiederherstellen.
Zusammengefasst in Kapitel 12 von: Ian Stewart: The Mathematics of Life, Profile, London 2011
Pascals Argumentation steht in mancher Hinsicht auf wackligen Füßen. Der wichtigste Einwand ist, dass sie für jedes beliebige hypothetische übernatürliche Wesen gelten würde.
Der Satz besagt, dass die Summe einer großen Zahl von Zufallsvariablen unter gewissen (recht gängigen) Bedingungen näherungsweise normalverteilt ist. Genauer gesagt: Wenn (x1, …, xn) eine Folge von unabhängigen, identisch verteilten Zufallsvariablen ist, jede mit dem Mittelwert µ und der Varianz ơ2, dann besagt der Zentrale Grenzwertsatz, dass die Verteilung der Zufallsvariablen
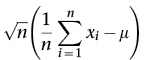
gegen eine Normalverteilung mit dem Mittelwert 0 und der Standardabweichung ơ konvergiert, wenn n beliebig groß wird.
Man stelle sich drei punktförmige Massen (auch Massenpunkt genannt), die durch n–1, n, n+1 nummeriert sind, auf einer waagerechten Linie positioniert vor. Zu einer späteren Zeit t seien sie un–1(t), un(t) und un+1(t) von ihren Anfangspositionen entfernt. Nach Newtons zweitem Bewegungsgesetz ist die Beschleunigung jedes Massenpunktes der Summe der auf ihn einwirkenden Kräfte proportional. Wir machen die vereinfachende Annahme, dass die senkrechten Auslenkungen der Massenpunkte sehr klein sind. Dann ist die Kraft, die Masse n–1 auf Masse n ausübt, in sehr guter Näherung proportional zu der Differenz un–1(t) – un(t), und analog ist die Kraft, die n + 1 auf n ausübt, zur Differenz un+1(t) – un(t) proportional. In der Summe wirkt auf die Masse n eine zu un–1(t) – 2un(t) + un+1(t) proportionale Kraft. Das ist die Differenz zwischen un-1(t) – un(t) und un+1(t) – un(t), und jede dieser Differenzen ist die Differenz zwischen den Positionen benachbarter Massen. Die Kraft auf Masse n ist also eine Differenz von Differenzen.
Nun wollen wir annehmen, dass die Massenpunkte sehr nahe beieinanderliegen. In der Analysis gilt eine Differenz – geteilt durch eine passend kleine Konstante – als Näherung für eine Ableitung. Eine Differenz von Differenzen ist eine Näherung für die Ableitung einer Ableitung, also einer zweiten Ableitung. Im Grenzfall unendlich vieler Massenpunkte, die unendlich dicht liegen, ist die Kraft auf einen Punkt deshalb  ; dabei ist x die Raumkoordinate längs der Saite. Nach Newtons zweitem Gesetz ist das proportional zur Beschleunigung des Punktes senkrecht zur Saite, also die zweite Zeitableitung
; dabei ist x die Raumkoordinate längs der Saite. Nach Newtons zweitem Gesetz ist das proportional zur Beschleunigung des Punktes senkrecht zur Saite, also die zweite Zeitableitung  . Bezeichnet man die Proportionalitätskonstante mit c2, erhält man die Gleichung:
. Bezeichnet man die Proportionalitätskonstante mit c2, erhält man die Gleichung:
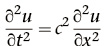
in der u(x, t) die senkrechte Position von Punkt x zur Zeit t angibt.
Eine Animation kann man sich auf http://en.wikipedia.org/wiki/Wave_equation anschauen.
Als Formel geschrieben, sehen die Lösungen so aus:

mit beliebigen Funktionen f und g.
Eine Animation der ersten Eigenschwingung einer runden Trommel findet man auf http://en.wikipedia.org/wiki/Vibrations_of_a_circular_drum Eine rechteckige Membran findet man animiert auf http://www.falstad.com/membrane/
Nehmen wir an  , dann gilt
, dann gilt
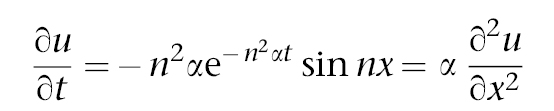
Also erfüllt u(x, t) die Wärmeleitungsgleichung.
Diese JFIF-Codierung ist im Netz gebräuchlich. EXIF-Codes, die man für Kameras verwendet, enthalten auch «Metadaten» über Kameraparameter wie Datum, Uhrzeit und Belichtungswerte.
http://www.nasa.gov/topics/earth/features/2010-warmest-year.html
Donald McDonald. How does a cat fall on its feet?, New Scientist 7 no. 189 (1960) 1647–9. Siehe auch http://en.wikipedia.org/wiki/Cat_righting_reflex
Die Rotation auf beiden Seiten der dritten Gleichung ergibt
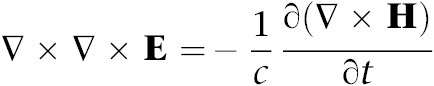
Die Vektoranalysis sagt uns, dass sich die linke Seite der Gleichung vereinfachen lässt zu
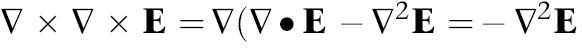
wobei wir auch die erste Gleichung benutzen. Hier ist  2 der Laplace-Operator. Mit Hilfe der vierten Gleichung ergibt sich für die rechte Seite
2 der Laplace-Operator. Mit Hilfe der vierten Gleichung ergibt sich für die rechte Seite
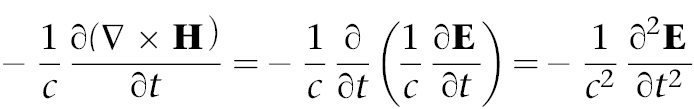
Kürzt man die Minuszeichen heraus und multipliziert mit c2, erhält man die Wellengleichung für E:
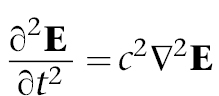
Ebenso lässt sich die Wellengleichung für H berechnen.
Speziell gilt
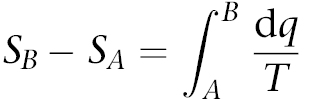
wobei SA und SB die Entropien der Zustände A und B sind.
Der zweite Hauptsatz der Thermodynamik ist fachsprachlich eine Ungleichung, keine Gleichung. Ich habe den zweiten Hauptsatz in das Buch aufgenommen, weil seine zentrale Stellung seine Einbeziehung verlangt. Es handelt sich zweifellos um eine mathematische Formel, eine lockere Interpretation von «Gleichung», wie sie außerhalb der wissenschaftlichen Fachliteratur weit verbreitet ist. Die Formel, auf die Anmerkung 32 Bezug nimmt und die ein Integral verwendet, ist eine echte Gleichung. Sie definiert die Änderung der Entropie, doch der zweite Hauptsatz sagt uns, was ihr wichtigstes Merkmal ist.
Brown wurde von dem niederländischen Physiologen Jan Ingenhousz vorweggenommen; dieser beobachtete dasselbe Phänomen bei Kohlenstaub, der auf der Oberfläche von Alkohol trieb, schlug aber keinerlei Theorie vor, um das Gesehene zu erklären.
Im Gran Sasso National Laboratory in Italien steht ein 1300-Tonnen-Teilchendetektor namens OPERA (oscillation project with emulsion-tracking apparatus).
Im Lauf von zwei Jahren hat OPERA 16000 Neutrinos aufgespürt, die im europäischen Labor für Teilchenphysik (CERN) in Genf erzeugt wurden. Neutrinos sind elektrisch neutrale subatomare Teilchen mit sehr geringer Masse, und sie können gewöhnliche Materie problemlos durchdringen. Die Ergebnisse waren verblüffend: Im Durchschnitt legten die Neutrinos den 730-Kilometer-Trip 60 Nanosekunden (Milliardstel Sekunden) schneller zurück, als sie es gekonnt hätten, wenn sie mit Lichtgeschwindigkeit gereist wären. Das stellte sich jedoch später als Messfehler heraus. Zwei Mitglieder des Forschungsteams sind deswegen von ihren Positionen als Sprecher und Projektleiter zurückgetreten (siehe z.B. http://www.sueddeutsche.de/wissen/cern-leitende-wissenschaftler-treten-wegen-neutrino-daten-zurueck-1.1324082).
Eine gründliche Erklärung findet sich auf der Website von Terence Tao: http://terrytao.wordpress.com/2007/12/28/einsteins-derivation-of-emc2/
Die Herleitung der Gleichung erfordert fünf Schritte:
(a) Man beschreibe, wie die Raum- und Zeitkoordinaten transformiert werden, wenn sich das Bezugssystem ändert.
(b) Mit Hilfe dieser Beschreibung berechne man, wie sich die Frequenz eines Photons ändert, wenn sich das Bezugssystem ändert.
(c) Mit Hilfe des Planck-Gesetzes berechne man, wie sich Energie und Impuls eines sich bewegenden Körpers beim Wechsel des Bezugssystems ändern.
(d) Man wende den Energie- und den Impulserhaltungssatz an, um zu berechnen, wie sich Energie und Impuls eines sich bewegenden Körpers ändern.
(e) Man lege den Wert einer ansonsten willkürlichen Konstanten in der Rechnung fest, indem man die Ergebnisse mit der Newton’schen Physik vergleicht, wenn die Geschwindigkeit des Körpers gering ist.
Ian Stewart und Jack Cohen. Figments of Reality, Cambridge University Press, Cambridge 1997, Seite 37.
http://en.wikipedia.org/wiki/Mass%E2%80%93energy_equivalence
Nicht alle sahen das so. Henry Courten, der Fotos von der Sonnenfinsternis 1970 neu analysierte, berichtete von mindestens sieben sehr kleinen Körpern, die sich in engen Bahnen um die Sonne bewegten – vielleicht ein Hinweis auf einen dünn bevölkerten inneren Asteroidengürtel. Bisher konnte ihre Existenz jedoch nicht schlüssig belegt werden, und ihr Durchmesser könnte nicht mehr als 60 Kilometer betragen. Bei den auf den Fotos zu erkennenden Objekten könnte es sich um kleine, gerade vorbeiziehende Kometen oder Asteroiden mit exzentrischen Umlaufbahnen gehandelt haben. Was auch immer sie waren, Vulkan waren sie nicht.
Die Vakuumenergie in einem Kubikzentimeter freien Raumes wird auf 10–15 Joule geschätzt. Der Quantenelektrodynamik zufolge sollte sie theoretisch 10107 Joule betragen – eine Abweichung um einen Faktor 10122. http://en.wikipedia.org/wiki/Vacuum_energy
Penroses Arbeit wird beschrieben in: Paul Davies. The Mind of God, Simon & Schuster, New York 1992 (deutsch: Der Plan Gottes, Insel, Frankfurt, 1996).
Joel Smoller und Blake Temple. A one parameter family of expanding wave solutions of the Einstein equations that induces an anomalous acceleration into the standard model of cosmology. http://arxiv.org/abs/0901.1639
R. S. MacKay und C. P. Rourke. A new paradigm for the universe, Vorabdruck, University of Warwick 2011. Genauere Informationen finden sich in den Artikeln, die unter http://msp.warwick.ac.uk/~cpr/paradigm/ aufgelistet sind.
Die Kopenhagener Deutung wird gewöhnlich auf Diskussionen zwischen Niels Bohr, Werner Heisenberg, Max Born und anderen Mitte der 1920er Jahre zurückgeführt. Sie verdankt ihren Namen der Tatsache, dass Bohr Däne war, doch keiner der beteiligten Physiker benutzte damals diese Bezeichnung. Don Howard hat vermutet, dass der Name und die Sichtweise, die er beinhaltet, erstmals in den 1950ern gebraucht wurden, wahrscheinlich von Heisenberg. Siehe D. Howard. ‹Who Invented the „Copenhagen Interpretation“? A Study in Mythology›, Philosophy of Science 71 (2004) 669–682.
Unsere Katze Harlequin kann häufig in einem Überlagerungszustand «schlafend» und «schnarchend» beobachtet werden, doch das zählt wohl nicht.
Zwei Science-Fiction-Romane zu diesem Thema sind Philip K. Dicks Das Orakel vom Berge und Norman Spinrads Der stählerne Traum. Der Roman des Thrillerautors Len Deighton, SS-GB, spielt ebenfalls in einem kontrafaktischen, von Nazis beherrschten England. Wenn es um das geistreiche Spiel mit alternativen historischen Entwicklungen geht, darf auch der deutsche Schriftsteller Carl Amery nicht unerwähnt bleiben. Amery hat sich verschiedentlich mit historischen «Paralleluniversen» auseinandergesetzt. (Zum Beispiel «Das Königsprojekt», «An den Feuern der Leyermark».)
Beim Würfeln weise ich die Symbole a, b, c folgendermaßen zu:
a Der Würfel zeigt 1, 2 oder 3
b Der Würfel zeigt 4 oder 5
c Der Würfel zeigt 6
a tritt mit Wahrscheinlichkeit ½ auf, b mit Wahrscheinlichkeit 1/3 und c hat die Wahrscheinlichkeit 1/6. Dann muss jede Formel für den Informationsgehalt den Wert H(1/2,1/3,1/6) ergeben, ganz gleich, wie sie aussieht.
Ich könnte mir das Experiment aber auch anders vorstellen. Zunächst entscheide ich, ob der Würfel etwas unter 4 oder nicht anzeigt. Nennen wir diese beiden Möglichkeiten q und r. Das heißt
q Der Würfel zeigt 1, 2 oder 3
r Der Würfel zeigt 4, 5 oder 6
q und r haben beide die Wahrscheinlichkeit ½. Ihr Informationsgehalt ist H(1/2,1/2). Fall q entspricht meinem ursprünglichen a, während Fall r b und c repräsentiert. Ich kann r aufteilen in b und c, und die Wahrscheinlichkeiten sind 2/3 und 1/3, unter der Voraussetzung, dass r eingetreten ist. Wenn wir uns nun auf diesen Fall beschränken, ergibt sich die Information, die durch b oder c übermittelt wird, als H(2/3,1/3). Shannon verlangt nun, dass die auf diese zwei verschiedenen Weisen übermittelte Information so zusammenhängt:
Siehe Abbildung 61.
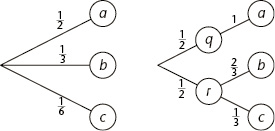
Abbildung 61: Wahlmöglichkeiten, auf verschiedene Weise kombiniert. Der Informationsgehalt sollte in beiden Fällen gleich sein.
Der Faktor ½ vor H tritt auf, weil der zweite Schritt nur in der Hälfte der Fälle eintritt, nämlich, wenn man bereits r gewählt hat. Vor dem H unmittelbar hinter dem Gleichheitszeichen gibt es diesen Faktor nicht, weil sich dieses H auf eine Wahl bezieht, die in jedem Fall getroffen wird – die zwischen q und r.
Siehe dazu Kapitel 2 in: C. F. Shannon and W. Weaver: The Mathematical Theory of Communication, University of Illinois Press, Urbana 1964.
Wenn die Population relativ klein ist, sodass xt nahe bei 0 liegt, liegt 1 – xt nahe bei 1. Die Größe der nächsten Generation liegt daher nahe bei kxt, ist also um den Faktor k größer als die gegenwärtige. Wenn die Populationsgröße zunimmt, verringert der Zusatzfaktor 1 – xt die aktuelle Wachstumsrate, und sie fällt auf 0, wenn die Population ihr theoretisches Maximum erreicht.
R. F. Costantino, R. A. Desharnais, J. M. Cushing und B. Dennis. Chaotic dynamics in an insect population, Science 275 (1997) 389–391.
J. Huisman und F. J. Weissing. Biodiversity of plankton by species oscillations and chaos, Nature 402 (1999) 407–410.
E. Benincà, J. Huisman, R. Heerkloss, K. D. Jöhnk, P. Branco, E. H. Van Nes, M. Scheffer und S. P. Ellner. Chaos in a long-term experiment with a plankton community, Nature 451 (2008) 822–825.
Der Wert einer Kaufoption ist
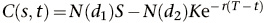
wobei


der Preis der zugehörigen Verkaufsoption ist
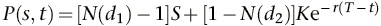
Hier bedeutet N(dj) die kumulierte Verteilungsfunktion der Standardnormalverteilung für j = 1,2, und T–t ist der Zeitpunkt der Fälligkeit.
Ganz korrekt heißt es: Schwedischer Reichsbankpreis in Wirtschaftswissenschaften im Gedenken an Alfred Nobel.
M. Poovey: Can numbers ensure honesty? Unrealistic expectations and the U.S. accounting scandal, Notices of the American Mathematical Society 50 (2003) 27–35.
A. G. Haldane and R. M. May: Systemic risk in banking ecosystems, Nature 469 (2011) 351–355.
«Um die mühsame Wiederholung der Wörter ‹ist das Gleiche wie› zu vermeiden, werde ich, wie ich es häufig bei meinen Arbeiten tue, zwei parallele Striche einsetzen oder zwillingshafte Linien gleicher Länge, weil keine zwei Dinge sich mehr gleichen können.»
Robert Recorde, Der Wetzstein des Wissens, 1557
Gleichungen sind das Lebenselixier von Mathematik, Naturwissenschaften und Technik. Ohne sie würde es unsere Welt in ihrer gegenwärtigen Form nicht geben. Gleichungen stehen jedoch in dem Ruf, abschreckend zu wirken: So erklärten Stephen Hawkings Verleger ihrem Autor, jede Gleichung werde den Verkaufserfolg seines Buches Eine kurze Geschichte der Zeit halbieren, ignorierten aber dann ihren eigenen Rat und erlaubten ihm, E = mc2 aufzunehmen, obwohl sie ohne die Formel doch angeblich weitere 10 Millionen Exemplare verkauft hätten. Ich bin auf Hawkings Seite. Gleichungen sind zu wichtig, um sie zu verstecken. Aber diese Verleger hatten auch in gewisser Weise recht: Gleichungen sind formal und streng, sie sehen kompliziert aus, und selbst diejenigen unter uns, die Gleichungen lieben, können verscheucht werden, wenn sie mit ihnen bombardiert werden.
In diesem Buch habe ich eine gute Entschuldigung. Da es ausdrücklich um Gleichungen geht, kann ich ebenso wenig vermeiden, Gleichungen aufzunehmen, wie ich ein Buch über Bergsteigen schreiben könnte, ohne das Wort «Berg» zu verwenden. Ich möchte Sie überzeugen, dass Gleichungen eine wichtige Rolle bei der Schaffung unserer heutigen Welt gespielt haben, von der Kartographie bis zum Navi, von Musik bis zum Fernsehen, von der Entdeckung Amerikas bis zur Erforschung der Jupitermonde. Zum Glück muss man kein wissenschaftliches Genie sein, um die Poesie und Schönheit einer guten, bedeutenden Gleichung schätzen zu können.
In der Mathematik gibt es zwei Typen von Gleichungen, die, oberflächlich betrachtet, sehr ähnlich aussehen. Der eine Typ stellt Beziehungen zwischen verschiedenen mathematischen Größen her: Die Aufgabe besteht darin nachzuweisen, dass die Gleichung wahr ist. Der andere Typ liefert Information über eine unbekannte Größe, und die Aufgabe des Mathematikers besteht darin, die Gleichung zu lösen – das Unbekannte bekannt zu machen. Die Unterscheidung ist nicht eindeutig, denn manchmal lässt sich dieselbe Gleichung auf beiderlei Weisen einsetzen, doch sie stellt eine nützliche Leitlinie dar. In diesem Buch werden Sie beide Typen finden.
Gleichungen in der reinen Mathematik gehören im Allgemeinen zum ersten Typ: Sie enthüllen wunderbare Muster und Regelmäßigkeiten. Sie sind gültig, weil es angesichts unserer Annahmen über die logische Struktur der Mathematik keine Alternative gibt. Der Satz des Pythagoras, der eine Gleichung darstellt, ausgedrückt in der Sprache der Geometrie, ist ein Beispiel. Wenn man Euklids Grundannahmen über Geometrie akzeptiert, dann ist der Satz des Pythagoras wahr.
Gleichungen in der angewandten Mathematik und in der mathematischen Physik gehören gewöhnlich zum zweiten Typ. Sie codieren Information über die wirkliche Welt; sie drücken Eigenschaften des Universums aus, die im Prinzip ganz anders hätten aussehen können. Newtons Gravitationsgesetz ist ein gutes Beispiel. Es sagt uns, wie die Anziehungskraft zwischen zwei Körpern von ihrer Masse und Entfernung abhängt. Die Lösung der resultierenden Gleichung sagt uns dann, wie die Planeten die Sonne umkreisen oder wie man eine Flugbahn für eine Raumsonde entwerfen sollte. Newtons Gesetz ist jedoch kein mathematisches Theorem; es stimmt aus physikalischen Gründen; es passt zu den Beobachtungen. Das Gesetz der Schwerkraft hätte auch anders aussehen können. Tatsächlich ist es anders: Einsteins Allgemeine Relativitätstheorie verbessert Newtons Gesetz, da sie einige Beobachtungen besser erklärt, während sie diejenigen unangetastet lässt, von denen wir bereits wissen, dass Newtons Gesetz gut auf sie passt.
Der Lauf der menschlichen Geschichte ist immer wieder durch eine Gleichung in eine andere Richtung gelenkt worden. Gleichungen verfügen über verborgene Macht. Sie enthüllen die innersten Geheimnisse der Natur. Unter diesem Blickwinkel sehen Historiker den Aufstieg und Fall von Zivilisationen gewöhnlich nicht. Könige und Königinnen und Kriege und Naturkatastrophen findet man in Geschichtsbüchern in Hülle und Fülle, doch Gleichungen sind dünn gesät. Das ist unfair. Zu viktorianischen Zeiten demonstrierte Michael Faraday in der Royal Institution in London Besuchergruppen die Verbindung zwischen Magnetismus und Elektrizität. Einer Anekdote nach fragte ihn der spätere Premierminister William Gladstone, ob daraus irgendwelche praktische Konsequenzen erwachsen würden. Wie es heißt (die Beweislage ist dünn, aber warum eine schöne Geschichte ruinieren?), soll Faraday ihm geantwortet haben: «Durchaus, Sir. Eines Tages werden Sie darauf Steuern erheben.» Falls er das wirklich gesagt hat, hatte er recht. James Clerk Maxwell verwandelte frühe experimentelle Beobachtungen und empirische Gesetze über Magnetismus in ein System von Gleichungen für den Elektromagnetismus. Zu den vielen Konsequenzen, die daraus erwuchsen, gehörten Radio, Radar und Fernsehen.
Eine Gleichung bezieht ihre Macht aus einer einfachen Quelle. Sie sagt uns, dass zwei Berechnungen, die unterschiedlich erscheinen, die gleiche Antwort haben. Das Schlüsselsymbol ist das Gleichheitszeichen, =. Der Ursprung der meisten mathematischen Symbole ist entweder im Nebel der Zeit verschollen oder so jung, dass es keinerlei Zweifel gibt. Das Gleichheitszeichen ist ungewöhnlich, da es 450 Jahre zurückdatiert, wir aber nicht nur wissen, wer es erfunden hat, sondern auch warum. Der Erfinder war Robert Recorde, der es 1557 in seinem Buch The Whetstone of Witte (Der Wetzstein des Wissens) einführte. Recorde verwendete zwei parallele Linien (er benutzte einen veralteten englischen Begriff, gemowe, was so viel wie «Zwilling» bedeutet), um mühsame Wiederholungen der Wörter ‹ist das Gleiche wie› zu vermeiden. Dieses Symbol wählte er, weil «keine zwei Dinge sich mehr gleichen können als Zwillinge». Recorde traf eine gute Wahl. Sein Symbol ist seit nun 450 Jahren in Gebrauch.
Die Macht einer Gleichung liegt in der philosophisch schwierigen Korrespondenz zwischen Mathematik, einer kollektiven Schöpfung des menschlichen Geistes und einer äußerlichen physischen Wirklichkeit. Gleichungen machen tief gehende Strukturen der Außenwelt erfassbar und geben ihnen eine Form. Dadurch, dass wir lernen, Gleichungen wertzuschätzen und die Geschichten zu lesen, die sie erzählen, können wir wichtige Merkmale der Welt um uns herum entdecken. Prinzipiell könnte es andere Möglichkeiten geben, dasselbe Ergebnis zu erreichen. Viele Menschen ziehen Wörter Symbolen vor; auch Sprache verleiht uns Macht über unsere Umgebung. Das Verdikt von Naturwissenschaften und Technik lautet jedoch: Wörter sind zu ungenau, und unser Sprachschatz ist zu begrenzt, um uns wirklich Zugang zu den tieferen Aspekten der Wirklichkeit zu eröffnen. Die menschliche Sprache ist zu stark durch Annahmen und Assoziationen gefärbt. Wörter allein können uns nicht die wesentlichen Einsichten liefern, die wir brauchen.
Gleichungen können es. Sie gehören seit Jahrtausenden zu den wichtigsten Triebkräften in der menschlichen Zivilisation. Unsere ganze Geschichte hindurch haben Gleichungen die Fäden in der Gesellschaft gezogen. Sicherlich im Verborgenen – doch der Einfluss war da, ob bemerkt oder unbemerkt. Dies ist die Geschichte des Aufstiegs der Menschheit, erzählt anhand von 17 Gleichungen.
Der Satz des Pythagoras

Was sagt sie uns?
Wie die drei Seiten eines rechtwinkligen Dreiecks zueinander in Beziehung stehen.
Warum ist das wichtig?
Sie stellt ein wesentliches Bindeglied zwischen Geometrie und Algebra dar und erlaubt uns, Entfernungen in Form von Koordinaten zu berechnen. Zudem hat sie die Trigonometrie inspiriert.
Was hat sie gebracht?
Landvermessung, Navigation und in neuerer Zeit die Spezielle und die Allgemeine Relativitätstheorie – die beiden gegenwärtig besten Theorien über Raum, Zeit und Schwerkraft.
Fordern Sie irgendeinen Schüler auf, einen berühmten Mathematiker zu nennen, und falls ihnen überhaupt ein solcher einfällt, werden die meisten sicherlich für Pythagoras optieren. Falls nicht, fällt vielleicht der Name Archimedes. Selbst der berühmte Isaac Newton spielt hinter diesen beiden Superstars der Antike nur die dritte Geige. Archimedes war ein intellektueller Riese, Pythagoras wahrscheinlich nicht, doch er verdient mehr Anerkennung, als er oft erhält. Nicht für das, was er geleistet hat, sondern für das, was er in Gang gesetzt hat.
Pythagoras wurde um 570 v. Chr. auf der griechischen Insel Samos in der östlichen Ägäis geboren. Er war Philosoph und Geometer. Das Wenige, was wir über sein Leben wissen, stammt von viel späteren Autoren, und wie historisch korrekt diese Informationen sind, ist fraglich, doch die wichtigsten Daten sind wahrscheinlich korrekt. Um 530 v. Chr. siedelte er wahrscheinlich nach Kroton über, einer griechischen Kolonie im heutigen Süditalien. Dort gründete er eine philosophisch-religiöse Schule, die Pythagoreer, die glaubten, das Universum basiere auf Zahlen. Der heutige Ruhm ihres Gründers beruht auf dem Satz, der seinen Namen trägt. Dieser Satz wird seit mehr 2000 Jahren gelehrt und hat Eingang in die Popkultur gefunden. In den Film Merry Andrew (1958), in dem Danny Kaye die Hauptrolle spielte, heißt es in einem Song:
Das Quadrat der Hypotenuse
Eines rechtwinkligen Dreiecks
Ist gleich
der Summe der Quadrate
der beiden anliegenden Seiten.
Der Song fährt mit einer doppeldeutigen Aufforderung fort, seine Partizipien nicht baumeln zu lassen, und verknüpft Einstein, Newton und die Gebrüder Wright mit dem berühmten Satz. Die beiden ersten rufen «Heureka!», nein, das war Archimedes. Sie merken schon, dass sich der Songtext nicht gerade durch historische Präzision auszeichnet, aber das ist nun mal Hollywood. In Kapitel 13 werden wir jedoch sehen, dass der Songtexter Johnny Mercier wahrscheinlich näher an Einstein dran war, als ihm bewusst war.
Der Satz des Pythagoras taucht im englischen Sprachraum in einem sehr bekannten Witz auf, der auf schrecklichen Kalauern über die Squaw auf dem Nilpferd (engl. hippopotamus, verballhornt Hypotenuse) basiert. Man findet den Witz überall im Internet, doch deutlich schwieriger ist es, seinen Ursprung zu finden.[1] Darüber hinaus gibt es Pythagoras-Cartoons, Pythagoras-T-Shirts und sogar eine griechische Briefmarke (Abbildung 1).

Abbildung 1: Griechische Briefmarke, die den Satz des Pythagoras illustriert.
Trotz all diesem Rummel wissen wir nicht, ob Pythagoras seinen Satz tatsächlich bewies. Tatsächlich wissen wir nicht einmal, ob der Satz von ihm stammt. Er könnte durchaus von einem seiner Schüler oder einem babylonischen oder sumerischen Schreiber entdeckt worden sein. Aber Pythagoras strich den Ruhm ein, und sein Name blieb damit verbunden. Welchen Ursprungs auch immer, der Satz und seine Konsequenzen hatten einen gewaltigen Einfluss auf die menschliche Geschichte. Sie öffneten buchstäblich unsere Welt.
Die Griechen drückten den Satz des Pythagoras nicht als Gleichung im modernen symbolischen Sinne aus. Das kam erst später mit der Entwicklung der Algebra. In der Antike wurde der Satz verbal und geometrisch formuliert. Eine elegante Form erhielt der Satz erst in den Schriften des Alexandriners Euklid, der auch den ersten, uns überlieferten Beweis führte. Um 250 v. Chr. wurde Euklid durch seine berühmten Elemente, das einflussreichste mathematische Lehrbuch aller Zeiten, zum ersten modernen Mathematiker. Euklid verwandelte Geometrie in Logik, indem er seine Grundannahmen explizit formulierte und dann benutzte, um all seine Sätze systematisch zu beweisen. Er baute einen begrifflichen und gedanklichen Turm, dessen Fundament Punkte, Linien und Kreise waren und dessen Zinnen aus genau fünf regelmäßigen Körpern bestand.
Eines der Juwelen in Euklids Krone war der Satz, den wir heute den Satz des Pythagoras nennen: Satz 47 aus Euklids Elementen lautet: In den rechtwinkligen Dreiecken ist das Quadrat, welches von der dem rechten Winkel gegenüberliegenden Seite beschrieben wird, den Quadraten, welche von den ihn einschließenden Seiten beschrieben werden, gleich.
Kein hippopotamus. Und auch keine Hypotenuse. Nicht einmal ein ausdrückliches «Summe» oder «addieren sich». Dennoch stellt der Satz des Pythagoras eindeutig eine Gleichung dar, da er das entscheidende Wort gleich enthält.
Was höhere Mathematik angeht, so arbeiteten die Griechen mit Linien und Flächen statt mit Zahlen. Daher hätten Pythagoras und seine griechischen Nachfolger den Satz als Gleichheit von Flächen formulieren können: «Die Fläche eines Quadrats, das mit Hilfe der längsten Seite eines rechtwinkligen Dreiecks konstruiert wird, ist die Summe der Flächen der Quadrate, die aus den beiden anderen Seiten gebildet werden.» Die längste Seite ist die berühmte Hypotenuse, was so viel bedeutet wie «die sich unten erstreckende [Dreieckseite]», wie es der Fall ist, wenn man das Diagramm in der geeigneten Orientierung zeichnet (Abbildung 2, links).
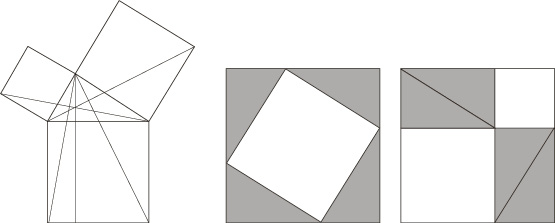
Abbildung 2: Links: Konstruktionsgeraden für Euklids Beweis des Satzes des Pythagoras. Mitte und rechts: Alternativer Beweis für den Satz. Die äußeren Quadrate haben die gleiche Fläche, und alle schattierten Dreiecke haben ebenfalls die gleiche Fläche. Daher hat das gekippte weiße Quadrat die gleiche Fläche wie die beiden anderen weißen Quadrate zusammen.
Innerhalb von nur 2000 Jahren ist der Satz des Pythagoras als algebraische Gleichung in eine neue Form gegossen worden:
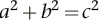
Dabei ist c die Länge der Hypotenuse, a und b sind die Längen der anderen beiden Seiten, und die kleine hochgestellte 2 bedeutet «zum Quadrat». Algebraisch ist das Quadrat einer jeden Zahl eben diese Zahl, multipliziert mit sich selbst, und wir wissen, dass die Fläche eines jeden Quadrats dem Quadrat der Länge seiner Seite entspricht. Daher sagt Pythagoras’ Gleichung, wie ich sie nun nennen will, dasselbe aus, was Euklid sagte – abgesehen von verschiedenen psychologischen Altlasten, die damit zu tun haben, wie man in der Antike über grundsätzliche mathematische Konzepte wie Zahlen und Flächen dachte, ein Thema, das ich an dieser Stelle nicht weiter vertiefen möchte.
Die Gleichung des Pythagoras hat viele Verwendungen und Konsequenzen. Ganz direkt erlaubt sie, die Länge der Hypotenuse zu berechnen, wenn die beiden anderen Seiten gegeben sind. Nehmen wir zum Beispiel an, dass a = 3 und b = 4 ist. Dann gilt: c2 = a2 + b2 = 32 + 42 = 9 + 16 = 25. Daher ist c = 5. Das ist das berühmte 3–4–5-Dreieck, das in der Schulmathematik allgegenwärtig ist und das einfachste Beispiel für ein pythagoreisches Tripel darstellt: eine Liste ganzer Zahlen, die die Gleichung des Pythagoras erfüllen. Das nächsteinfache Tripel ist, abgesehen von skalierten Versionen wie 6–8–10, das 5–12–13-Dreieck. Es gibt unendlich viele solcher Tripel, und die Griechen wussten, wie man sie konstruiert. Derartige Tripel sind in der Zahlentheorie noch immer von gewissem Interesse, und selbst in den letzten zehn Jahren sind neue Eigenschaften entdeckt worden.
Statt c mit Hilfe von a und b zu bestimmen, kann man indirekt vorgehen und die Gleichung nach a auflösen, wenn b und c bekannt sind. Man kann auch subtilere Fragen beantworten, wie wir gleich sehen werden.
Warum ist der Satz wahr? Euklids Beweis ist ziemlich kompliziert und erfordert, im Diagramm in Abbildung 2 (links) fünf zusätzliche Linien zu ziehen und sich auf mehrere bereits zuvor bewiesene Sätze zu stützen. Viktorianische Schuljungen (damals gab es nur wenige Mädchen, die sich mit Geometrie beschäftigten) bezeichneten das Diagramm wenig ehrerbietig als «Pythagoras’ Hosen». Ein direkter und intuitiver, wenn auch nicht sehr eleganter Beweis benutzt vier Kopien des Dreiecks, um zwei Lösungen desselben mathematischen Puzzles zu verknüpfen (Abbildung 2, rechts). Das Bild ist überzeugend, doch die Ergänzung der logischen Details erfordert einiges an Nachdenken. Woher wissen wir zum Beispiel, dass die gekippte weiße Figur in der Mitte des Bildes ein Quadrat ist?
Vieles spricht dafür, dass der Satz des Pythagoras schon lange vor Pythagoras bekannt war. Ein babylonisches Tontäfelchen[2] im Britischen Museum enthält in Keilschrift ein mathematisches Problem und seine Antwort, die man etwa so übersetzen könnte:
4 ist die Länge und 5 die Diagonale. Was ist die Breite?
4 mal 4 ist 16.
5 mal 5 ist 25.
Nimm 16 von 25 und übrig bleiben 9.
Wie oft muss ich welche Zahl malnehmen, um 9 zu erhalten?
3 mal 3 ist 9.
Daher ist 3 die Breite.
Deshalb kannten die Babylonier zweifellos das 3-4-5-Dreieck, und das bereits 1000 Jahre vor Pythagoras.
Ein anderes Täfelchen, YBC 7289 aus der babylonischen Sammlung der Yale University, zeigt Abbildung 3 (links). Zu sehen ist das Diagramm eines Quadrats mit einer Seitenlänge von 30, dessen Diagonale zwei Zahlenlisten trägt: 1, 24, 51, 10 und 42, 25, 35. Die Babylonier benutzten eine auf der Zahl 60 basierende Notation, daher liest sich die erste Liste tatsächlich als 1 + 24/60 + 51/602 + 10/603, was, in Dezimalzahlen ausgedrückt, 1,4142129 ist. Die Quadratwurzel von 2 ist 1,4142135. Die zweite Liste entspricht dem 30-Fachen dieses Werts. Also wussten die Babylonier, dass die Diagonale eines Quadrats gleich der Seitenlänge multipliziert mit der Quadratwurzel von 2 ist. Da 12 + 12 = 2 = (√2)2 ist, ist dies ebenfalls ein Beispiel für den Satz des Pythagoras.

Abbildung 3: Links: YBC 7289. Rechts: Plimpton 322.
Noch bemerkenswerter, wenn auch rätselhafter, ist die Tontafel Plimpton 322 aus der George-Arthur-Plimpton-Sammlung der Columbia University (Abbildung 3, rechts). Es handelt sich um eine Tabelle mit vier Spalten und 15 Zeilen. Die letzte Spalte listet lediglich die Zeilenzahlen auf, von 1 bis 15. Im Jahr 1945 haben die Wissenschaftshistoriker Otto Neugebauer und Abraham Sachs[3] festgestellt, dass das Quadrat der Zahl (nennen wir es c) in der dritten Spalte minus dem Quadrat der Zahl (nennen wir es b) in der zweiten Spalte in jeder Zeile selbst ein Quadrat (nennen wir es a) ist. Daraus folgt a2 + b2 = c2; daher enthält die Tafel offenbar pythagoreische Tripel. Zumindest ist das der Fall, wenn man vier offensichtliche Fehler korrigiert. Dennoch ist nicht absolut sicher, dass Plimpton 322 etwas mit pythagoreischen Tripeln zu tun hat, und selbst wenn das der Fall sein sollte, könnte es lediglich eine bequeme Liste von Dreiecken gewesen sein, deren Fläche leicht zu berechnen war. Diese könnten dann gesammelt worden sein, weil sie gute Näherungswerte für andere Dreiecke und Formen lieferten, beispielsweise im Rahmen von Landvermessungen.
Eine andere herausragende antike Zivilisation ist die des alten Ägypten. Einiges spricht dafür, dass Pythagoras als junger Mann Ägypten besucht hat, und einige Historiker vermuten, dass er dort auf seinen Satz gestoßen ist. Die Berichte ägyptischer Mathematiker, die bis in unsere Zeit überdauert haben, stützen diese Vermutung kaum, doch ihre Zahl ist recht gering. Oft wird – in der Regel im Zusammenhang mit den Pyramiden – darauf verwiesen, dass die Ägypter rechte Winkel mit Hilfe des 3-4-5-Dreiecks konstruierten, indem sie ein Seil mit 12 Knoten in gleichen Abständen entsprechend auslegten, und Archäologen solche Seile gefunden hätten. Beide Behauptungen ergeben jedoch nicht viel Sinn. Eine solche Technik wäre nicht sehr zuverlässig gewesen, denn Seile kann man dehnen und die Knotenabstände hätten sehr genau eingehalten werden müssen. Die Präzision, mit der die Pyramiden von Gizeh errichtet worden sind, ist allem überlegen, was man mit einem solchen Seil hatte erreichen können. Weitaus praktischere Werkzeuge, ähnlich dem Winkel eines Zimmermanns, sind gefunden worden. Ägyptologen, die auf antike ägyptische Mathematik spezialisiert sind, kennen keine Berichte, die besagen, dass Seile oder Schnüre verwendet wurden, um ein 3-4-5-Dreieck zu konstruieren, und es gibt keine Beispiele für solche Seile. Daher ist diese Geschichte, so hübsch sie auch sein mag, höchstwahrscheinlich eine Legende.
Wenn wir Pythagoras in unsere moderne Welt versetzen könnten, würde er viele Unterschiede zwischen damals und heute feststellen. In seiner Zeit war das medizinische Wissen rudimentär, künstliches Licht spendeten nur Kerzen und Fackeln, und die schnellste Form der Kommunikation war ein berittener Bote oder ein Leuchtturm auf einem Hügel. Die damals bekannte Welt umfasste einen großen Teil von Europa, Asien und Afrika – aber weder Nord- und Südamerika noch Australien, die Arktis oder die Antarktis. Viele Kulturen hielten die Welt für flach: eine runde Scheibe oder sogar ein Quadrat, das nach den vier Himmelrichtungen ausgerichtet war. Trotz der Entdeckungen in der klassischen griechischen Antike war diese Überzeugung im Mittelalter noch weit verbreitet, wie sich an den orbis-terrae-Karten (Erdkreiskarten) ablesen lässt (Abbildung 4).

Abbildung 4: Weltkarte, die der marokkanische Kartograph al-Idrisi für König Roger II. von Sizilien um 1100 anfertigte.
Wer erkannte als Erster, dass die Welt rund war? Laut Diogenes Laertios, einem griechischen Biographen im 3. Jahrhundert, war es Pythagoras. In seinem Buch Leben und Meinungen berühmter Philosophen, einer Sammlung von Aussprüchen und biographischen Anmerkungen, die eine unserer Hauptquellen für das Privatleben der altgriechischen Philosophen ist, schrieb er: «Pythagoras war der Erste, der die Welt rund nannte, auch wenn Theophrastos dies Parmenides zuschreibt und Zenon Herodot.» Die alten Griechen behaupteten ganz unabhängig von den historischen Fakten gern, dass wichtige Entdeckungen von ihren berühmten Vorfahren gemacht worden seien, daher sollten wir diese Behauptung nicht unbesehen übernehmen, doch unbestritten ist, dass vom 5. Jahrhundert v. Chr. an alle angesehenen griechischen Philosophen und Mathematiker von der Kugelgestalt der Erde überzeugt waren. Diese Vorstellung scheint tatsächlich um die Zeit des Pythagoras aufgekommen zu sein und könnte auf einen seiner Anhänger zurückgehen. Aber es könnte sich auch um Allgemeinwissen gehandelt haben, das auf Hinweisen wie dem runden Schatten der Erde auf dem Mond bei einer Mondfinsternis oder auf einer Analogie zu dem offensichtlich runden Mond basierte.
Aber selbst für die Griechen war die Erde das Zentrum des Universums, und alles drehte sich um sie. Navigiert wurde nach ungefähren Berechnungen: Nachts orientierte man sich an den Sternen, tagsüber folgte man der Küstenlinie. Pythagoras’ Gleichung änderte das alles. Sie eröffnete der Menschheit den Weg zum heutigen Verständnis der Geographie unseres Planeten und seines Platzes im Sonnensystem. Es war der erste entscheidende Schritt in Richtung auf geometrische Methoden, wie man sie für Kartographie, Navigation und Landvermessung braucht. Diese Gleichung lieferte zugleich den Schlüssel zu einer entscheidend wichtigen Beziehung zwischen Geometrie und Algebra. Diese Entwicklungslinie führt von der Antike geradewegs zur Allgemeinen Relativitätstheorie und zur Kosmologie (siehe Kapitel 13). Pythagoras’ Gleichung eröffnete dem menschlichen Entdeckungsdrang im übertragenen wie auch im wörtlichen Sinne völlig neue Möglichkeiten. Sie enthüllte die Form unserer Welt und zeigte uns unseren Platz im Universum.
Viele der Dreiecke, auf die wir im realen Leben treffen, sind nicht rechtwinklig, daher mag die direkte Anwendbarkeit der Gleichung begrenzt erscheinen. Doch jedes Dreieck lässt sich in zwei rechtwinklige Dreiecke zerlegen (Abbildung 6), jede polygonale Form in Dreiecke. Daher nimmt die Gleichung a2 + b2 = c2 eine Schlüsselstellung ein: Sie beweist, dass eine nützliche Beziehung zwischen der Form eines Dreiecks und den Längen seiner Seiten besteht. Das Gebiet, das sich aus dieser Erkenntnis entwickelte, ist die Trigonometrie, die Dreiecksmessung.
90A5a, bc