Cover

There have been numerous books written about the history of mathematics, ranging from very brief introductions to extensive in-depth textbooks. This book is intended to provide a brief overview of the history of mathematics in a straightforward and understandable manner. By no means will this book cover the history of mathematics exhaustively or every mathematician whose work contributed to the evolution of mathematics. However, it will address major findings that influenced the development of mathematics as a coherent discipline.

Many books focus heavily on complicated mathematics, which is not easy to understand by many readers outside the discipline. The intention of this book is to present considerable mathematical content in an easy-to-digest manner. Moreover, this book will emphasize the historical foundations and background of the history of mathematics in order to provide context. There will be more mathematics content presented regarding the earlier historical periods because the mathematics discussed will be easier to understand for most readers, as opposed to its later developments. The mathematics presented in recent history would require advanced knowledge in the subject. Occasionally, however, this book will address mathematics that may assume prerequisite knowledge that may not be possessed by all readers. It is the author's belief that such an instance will rarely be encountered by most readers who have a high school background in mathematics and perhaps some college mathematics background as well. Readers who have been exposed to some calculus will have little to no trouble understanding the mathematics in this book. Hence, this book is written for a wide audience of readers. Readers with a range of basic high school or college mathematics backgrounds as well as students majoring in mathematics and high school mathematics teachers will find most of this book interesting and enjoyable. This book can be used as a textbook in a history of mathematics college class or even for pleasure reading and intellectual curiosity. Even a doctorate in the field may want to keep this book on hand as a quick reference guide. Middle school, high school, and college professors, and even elementary school teachers, may find this book useful in motivating their students to learn mathematics content through the use of mathematics history in their teaching. In order to be an effective teacher, it is important to engage students in the material. Introducing the history of mathematics can make the study of mathematics more enjoyable and help students see how mathematics developed throughout the centuries because it gives mathematics a human face. This book integrates formal history with anecdotes and legends, where appropriate, in order to make the reading more interesting. Even for the mathematical legends unlikely to be true, they have been constructed around significant historical figures and will be of interest to the reader. The reader will be notified when an anecdote or legend is merely speculative.

Another purpose of this book is to highlight the contributions made by various world cultures. The most recent books about the history of mathematics certainly have gone in this direction, but this book is intended to help the reader understand developments of mathematics around the world. Specifically, there are chapters presented on African, Egyptian, Babylonian, Chinese, Indian, Islamic, and Pre-Columbian American mathematics. It is important that students understand that mathematics has developed throughout the world and that no single culture has a monopoly on the subject. While there were remarkable mathematical developments in ancient Greece and throughout Europe in the Modern Era, these accomplishments would not have been possible without the contributions from various cultures such as Babylonian, Indian, and Islamic cultures. At the time Europe was in the “Dark Ages,” particularly in mathematics and science, great accomplishments were being made in China, India, and later the Middle East. It is commonly believed that much of modern mathematics was exclusively developed in Europe, but that is not the case. As addressed in this book, many of the concepts discovered by Europeans in the 17th to 19th centuries were discovered in some form, although often but not always more limited, much earlier in China, India, and the Middle East. Rich mathematical knowledge was also produced in parts of the Pre-Columbian Americas. This book will demonstrate that Indian and Islamic mathematics were highly influential on European mathematics, which began to more fully develop in the European Renaissance and would climb to remarkable heights throughout the 17th to 19th centuries.

Students from diverse cultures and backgrounds who believe that mathematics is an exclusively white male endeavor are less likely to be engaged in mathematics class. In fact, in a study in which children were asked to draw a mathematician, many children drew the stereotypical mathematician as an older white male. Nevertheless, after bringing diverse mathematicians into the classroom to speak with the children, many children drew diverse mathematicians of different backgrounds when asked to complete the task again.

While it is important for students to perform well in mathematics for its own sake, it is essential that students perform well because it serves as the “gatekeeper” for entrance to quality colleges and high paying careers. Success in mathematics is one of the strongest variables in predicting success in life. High paying careers such as those of mathematician, actuary, statistician, and engineer all require high levels of mathematics knowledge. Strong mathematics knowledge is also necessary for personal success and in making informed life decisions, including important economic, social, and political choices. Mathematics knowledge is a necessary component of financial literacy and economic well-being, and quantitative reasoning is needed for citizens to make informed decisions in a healthy democracy. Engagement in mathematics will lead to greater learning in mathematics, and teaching students by using mathematics history as a framework can also help facilitate the necessary student motivation needed for academic success.

The history of mathematics is intriguing because it gives us a perspective of the long development of mathematical ideas throughout the ages. It allows us to glimpse into the ancient cultures and place mathematics in the context of human history and development. It helps us realize that mathematics was discovered by real people, but simultaneously mathematics reveals universal truths. Unlike other subjects that depend on subjective information, mathematics objectively tells us about the world and the universe. Once a mathematical theorem is proved correctly, it is proved for the ages. People who enjoy history can gain a positive disposition toward mathematics if the subject is presented in its historical context. Mathematics is developed and interpreted by humans throughout the ages, which makes the study of its development a worthy goal.

Mathematics can be defined as the study of patterns in the context of quantity, structure, and dimension. Throughout this book, we shall take a journey throughout time and observe how people around the world have understood these patterns of quantity, structure, and dimension around them. We shall explore mathematics in the wider historical context. This book is set up in chronological order, for the most part, beginning with the earliest known records of human mathematics in Africa. It continues with ancient Egypt and Babylon, and then covers ancient Greece to the fall of the Roman Empire. We then turn to historical developments of mathematics in ancient to medieval China and India, and on to the Islamic world. Next, the mathematics of the Pre-Columbian Americas is explored. We then go into the dark period of mathematics in Europe after the fall of the Roman Empire until the influence of Islamic mathematics on European thinking. We next visit the European Renaissance and work our way through the 17th to 19th centuries in Europe. The 20th century takes us through Europe and to North America, which took the lead in mathematics after World War II. We shall then work our way to the early 21st century. Finally, we shall explore the history of mathematics education and its development in the United States during the 20th and 21st centuries.

A final note should be made regarding the source of the information in this book. This book was written from the class notes used in a mathematics history class taught by the author. This work is considered to be a textbook of information and not an original work of historical or mathematical research. The facts have been gathered from many other sources, and none of the information presented will be an original discovery by the author, besides the occasional author speculation. Facts found in one source were checked against the same facts in other sources, when available. As a textbook written for informative purposes, references are not cited throughout the book. The Resources and Recommended Readings section at the end of this book lists all of the sources in which information was gathered. In particular, a special note should be made about the University of St. Andrew's MacTutor History of Mathematics website. This website has proven to be an invaluable source of information on the backgrounds of the numerous mathematicians found in this book. For more details than this book can provide, it is recommended that the reader explore the MacTutor website for more information. As noted throughout the text, the Internet will continue to change how we live, work, and study. Now, more than any time in the past, the reader has access to an unlimited amount of information through simply having a computer and access to the Internet. This brief book should serve as a guide through mathematics history. It places the history in context and allows the reader to have a starting point for further exploration.

Humanity likely originated in Africa several million years ago as it separated from the common ancestor that we share with chimpanzees. Homo erectus migrated to Asia, while Homo neanderthalensis, or the Neanderthals, migrated to Europe. However, those whom are considered to be humans today, Homo sapiens, actually originated in Africa 200,000 years ago and eventually replaced H. erectus and H. neanderthalensis in Asia and Europe. Our ideas of what we consider to be typically recognizable human characteristics, such as reliance on speech and abstract thought, places humans around 50,000 years ago.

It is commonly believed that humanity first evolved in the eastern regions of Africa in today's nations of Ethiopia and Kenya. Researchers have followed humanity's migration and settlements into Asia and Europe, across the Indonesian archipelago into Australia and over the Bering Straight into the Americas. Not surprisingly, mathematics developed in a similar manner. The earliest known mathematical object is the Lebombo bone found in the 1970s, which is estimated to have originated around 37,000 years ago in Swaziland in southern Africa and is named after the Lebombo Mountains. Found in the Border Cave, the Lebombo bone is a tally stick with 29 notches that may have marked the lunar calendar. The Ishango bone was found in the Ishango area of the Congo in 1960 and indicates prime numbers, positive integers that have only two unique factors, between 10 and 20, and a lunar calendar like the Lebombo bone. There has been speculation that the first tally sticks indicate a lunar calendar for the purpose of predicting female menstruation cycles, which means African females may have been the first to create mathematical instruments and history recognizes them as the earliest mathematicians. The Ishango bone was found by Belgian geologist Jean de Heinzelin de Braucourt and may be about 20,000 years old. Both the Lebombo and Ishango Bones are made from the fibula, or calf bone, of a baboon. Today, the Ishango bone is on display at the Royal Belgian Institute of Natural Sciences in Brussels, Belgium.

There is also evidence of the early use of tally sticks in Europe. In 1937, the Wolf bone was found in Czechoslovakia by Karl Absolon, which may be up to 30,000 years old. It had 55 notches set in groups of five. The first 25 notches are separated from the other 30 notches by having one notch double in size from the others. Also found in Europe, the famous Lascaux Cave paintings are a collection of cave images found in southwestern France in 1940. The paintings mainly depict humans and animals, but may also have indicated a lunar calendar with 29 markings. In 1950, Willard Libby, who discovered carbon-14 dating and received the Nobel Prize for it in 1960, famously dated the Lascaux Cave paintings. Libby found that there was only 15% of carbon-14 present, as would be found in plant-based paint in 1950. The formula for exponential decay is A = Pe^kt, where A is the new amount, in this case the amount of carbon-14, P is the original amount, k is the decay constant, t is the time elapsed, and e is Euler's number, which is approximately 2.7182818285. By knowing the half-life of carbon-14 to be roughly 5700 years, one could reason that since in 5700 years, we would have half of the carbon-14 present left from when an organic life-form died, in this case the planets that made up the plant-based paint, we can find the decay constant because 0.5P = Pe^k⁽⁵⁷⁰⁰⁾. Solving for k gives us 0.5 = e⁵⁷⁰⁰^k. Taking the natural logarithm of both sides of the equation gives us ln(0.5) = 5700k, and k is approximately equal to –0.0001216. Since Libby had found that only 15% of the original carbon-14 was present, we have 0.15P = Pe^–0.0001216^t. Solving for t gives us 0.15 = e^–0.0001216^t. Taking the natural logarithm of both sides of the equations gives us ln(0.15) = –0.0001216t, and t is approximately equal to 15,600. This means the paint originated 15,600 years before 1950, which was 13,650 BCE.

The people who used the tally sticks were likely nomadic hunter–gatherers because they did not transition into an agricultural lifestyle, domesticating animals and plants, until about 10,000 years ago. It is argued that the shift from nomadic hunting–gathering to an agriculturally based system allowed for great social change for early humans. Since people became more sedentary, they gained the opportunity to begin the development of permanent settlements and stable civilizations. In fact, it is the environmental factors of good agricultural land, along with animals that are easy to domesticate, that has led noted physiologist and geographer Jared Diamond to conclude that history's most successful societies can be explained by access to these benefits.

As we shall see in later chapters, not all societies utilized the base 10 system, a system in which there are nine digits representing 1–9, a symbol for zero, and the number 10 being represented through the positioning of 1 and zero. Additionally, as we shall see, the zero took a very long time in development in human history. However, it should not be surprising that many societies, including our own modern societies throughout most of the world today, use base 10. Early humans had noticed that there was great convenience in using their fingers for counting and basic arithmetic, as many children and adults do today. Therefore, it made sense to consider the first 10 numbers as the foundation for a number system.

When numbers exceeded the number of fingers on human hands, people could turn to counting on their toes, which certainly becomes more cumbersome, but has been done in some civilizations. Another level of sophistication would be the use of the tally sticks, such as the use of the Lebombo, Ishango, and Wolf tally sticks.

For the ancient people, the next important use of mathematics was in their astronomical observations for religious purposes and tracking calendars, which would have often been connected in the celebration of holy days. Early humans, like humans of today, were fascinated by the night sky. There is mathematical regularity in the patterns found in observing the heavens. Calendar records have naturally arisen indicating each day that is designated by the rotation of the Earth, the monthly cycles of the Moon, and the yearly revolution around the Sun. We see evidence in the way the night sky influenced early mathematics in ancient Egypt, Babylon, China, India, and Greece. As humans developed stable agricultural societies, ruling and priestly classes began to develop due to societal surplus of goods. These classes would find the time to develop the mathematics of calendars for religious observances. Mathematics evolved for practical purposes such as civil affairs, including taxation, and better agricultural techniques. However, the night sky and its regularity could be considered an early birthplace of mathematics.

There is a connection between the night sky and religion. Early humans looked to the stars to find the divine. Today, this is manifested in the childhood belief in and our poetic fascination with Heaven residing in the clouds. For many cultures, the gods were found in constellations and planets. In school today, many students study the Greek names of constellations, and, even today, the planets in our solar system are named after the Greek and Roman gods. Jupiter is a Roman god, who is the greatest of gods, and equivalent to the Greek's Zeus. Saturn is the Roman equivalent to the Greek's Kronos, Neptune is the Greek's Poseidon, and Uranus is the name of a Greek god who is the father of Kronos and grandfather of Zeus. Pluto, no longer considered a planet, is the Roman name for the Greek's Hades. For the inner planets, Mercury is the Greek's Hermes, Venus is the Greek's Aphrodite, and Mars is the Greek's Ares.

The author of this book has always been fascinated by the constellations and night sky, and finds it appropriate that we can find such a connection between mathematics and the early civilizations. In a world that is ever changing as humans shape the landscape and environment around them, we can take comfort in the knowledge that when we gaze on the night sky, we are essentially viewing what ancient civilizations before us had viewed.

Ancient Egyptian society was centered on the Nile River and started when the people of the region began a sedentary agricultural lifestyle using the Nile to cultivate their farmlands, which was approximately 10,000 years ago. Prior to this time, the people of the region were nomadic and lived in what is now the Sahara Desert. Desertification began around 10,000 years ago, culminating in the formation of the Sahara Desert around 4,500 years ago. Egypt became a unified state around 3150 BCE when the Upper and Lower Nile valleys joined together under the first pharaoh, Menes, which began the Early Dynastic Period. The ancient Egyptian period ends with the Roman conquest in 30 BCE, and pharaoh rule ceased with Cleopatra as the last pharaoh. The Roman Republic became the Roman Empire 3 years later when Caesar Augustus became Emperor of Rome.

The ancient Egyptians are recognized for their great accomplishments in architecture, irrigation, agriculture, art, literature, and mathematics. When considering their circumstances, it is reasonable that the Egyptians would develop their culture in the chronology that they did. When people began living a sedentary agricultural lifestyle, they began to create stable villages and towns in which it was possible to build on their accomplishments and transmit knowledge to the next generation. Additionally, the wealth obtained from agriculture created need for various occupations that would require mathematical calculations for wages, architecture, and other measurements.

Egyptians needed mathematics for the creation of their calendars, which had 12 months with 30 days in each month; within each month, there were 3 weeks consisting of 10 days. The remaining 5 days were feast days at the end of the year. The Egyptians had 24 hours in a day with 12 hours for day and 12 hours for night. Twelve was a significant number for the Egyptians because they counted using the knuckles on their four fingers on one hand and each of the four fingers has three knuckles. Moreover, 12 is a convenient number given the number of factors it has.

The calendar proved useful for cultivating agriculture because the Egyptians were able to predict the best time for planting their crops and the cycles based on the flooding of the Nile River. Astronomy is directly related to calendar calculations, and as we shall see later with the Greeks, astronomy played a major role in early developments of mathematics.

A lasting legacy of Egyptian accomplishments is the pyramids, specifically the Pyramids of Giza. The Early Dynastic Period ended around 2800 BCE when the Old Kingdom Period began. It was during this time that the king became regarded as a living god and the pyramids were built. The Great Pyramid of Giza, also called the Pyramid of Khufu, was built in 2550 BCE and remains the only surviving ancient wonder of the world. It remained the tallest human-made structure until 1311 CE when the Lincoln Cathedral was built in England. The pyramids are a remaining legacy of Egyptian innovation in architecture and mathematics, and it was during this period that Egypt experienced great accomplishments in culture, art, and architecture. The Old Kingdom Period ended around 2300 BCE.

The Egyptians used the base 10 system. A number such as 432 would be expressed as four 100s, three 10s, and two 1s. However, unlike our current base 10 system, the Hindu–Arabic numeral system, the Egyptian system was neither multiplicative nor positional, but it was merely additive. That means there was no way of easily representing 800 without writing 100 eight times. In our modern system, we can represent 800 as 8 × 100, so we can see why our system is considered multiplicative. Our system is positional because we do not have to write 823 as 8 × 100 + 2 × 10 + 3 × 1, but rather we know the position of the individual digits represents hundreds, tens, and ones. For example, 823 is quite different from 382. In the first number, we know we have eight 100s, two 10s, and three 1s. In the latter number, we have three 100s, eight 10s, and two 1s. For us, it is the position of the digits that makes the difference. Using the Egyptian system, we would have to represent 823 by writing 100 eight times, 10 two times, and 1 three times. Using Egyptian symbols, we would have the following (see Table 2.1):

TABLE 2.1 Egyptian Numerals

Number	Egyptian symbol	Description
1		Staff
10		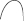Heel bone
100		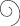Coil of rope
1000		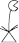Water lily (or lotus flower)
10,000		Finger
100,000		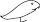Tadpole
1,000,000		Person with arms raised

It is quite straightforward to add or subtract using the Egyptian system. For addition, let us say we have 15 + 27. We would realize that we now have three 10s and twelve 1s. In other words, we have 3 heel bones and 12 staffs. However, if we replace 10 of those staffs with a heel bone, we now have 4 heel bones and 2 staffs.

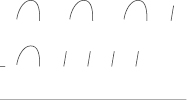
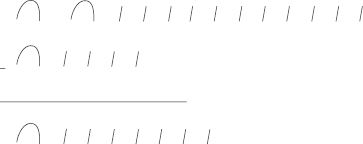
If we were to subtract two numbers, such as 14 from 31, we would immediately realize we cannot subtract the four staffs from the one staff. We would replace one of the three heel bones in 31 with 10 staffs to yield 11 – 4 = 7. Now, we only have two heel bones left from the 31 so we would have two heel bones minus one heel bone from the 14. Hence, our answer would be 17. See the illustration.

This is equivalent to the following.

The Egyptians had a very interesting method for multiplication. In order to understand their method, we must first understand a remarkable discovery made by this ancient civilization. The Egyptians knew that any integer could be written as the sum of powers of 2 without repeating any of the numbers. For example, we know that 5 = 1 + 4 and 13 = 1 + 4 + 8. The aspect of doubling may have originated in parts of Africa, south of Egypt. We shall use this rule to multiply later.

In one column, we list the powers of 2: 1, 2, 4, 8, 16, 32, … until we get as close to the smaller number as possible. In the right column, we start with the larger number and keep doubling. We want to find the sum of numbers in the left column that sum to the smaller number. We match those numbers with the right column and add the right column numbers together. This will be our answer. For example, 18 × 23 could be done as follows:

1	23
2	46
4	92
8	184
16	368

It is important to notice that 2 + 16 = 18. Therefore, we simply need to add 46 and 368 to yield the answer for 18 × 23, and we get 414. This works using the distributive property because we essentially have 23 × (2 + 16) to get 23 × 2 + 23 × 16. Recall that the distributive property indicates that a(b + c) = ab + ac.

The Egyptian method for multiplication is still taught in schools today as an alternative to the traditional algorithm of multiplication that many people in the United States learned in school. Everyday Mathematics, a book from the University of Chicago School Mathematics Project, teaches students the Egyptian method.

The Egyptians performed division problems in the same way, for the most part. The left column would be the same as multiplication, but the right column would have consecutive doublings of the smaller number until we reach the larger number. For example, 285 ÷ 15 would be as follows:

1	15
2	30
4	60
8	120
16	240

It is important to notice in the right column that 15 + 30 + 240 = 285, the larger number. Therefore, we simply need to add 1, 2, and 16 to yield the answer for 285 ÷ 15, and we get 19.

Ancient Egyptians used only unit fractions with the exception of 2/3 and 3/4, which had special symbols as well as a special symbol for 1/2. A unit fraction is a fraction with 1 in the numerator in the form 1/x, in which x is a nonzero integer. This means that 2/3 and 3/4 were the only nonunit fractions considered by the Egyptians. We could represent fractions such as 7/12 as the sum of other unit fractions. In this case, we would have 1/3 + 1/4. The procedure we can use to find the sums of unit fractions is to find all of the factors of the denominator. In our example, we could list the factors of 12: 1, 2, 3, 4, 6, and 12. We need to find the factors that sum to 7, which would be 3 and 4. Next we write 4/12 + 3/12 to yield 1/3 + 1/4. If this procedure does not work, such as in the case of 3/5, we can find an equivalent fraction such as 6/10, and then use the factors of 10 that sum to 6, which would be 5 and 1. Next we write 5/10 + 1/10 to yield 1/2 + 1/10. Finally, if all else fails, we could simply multiply the denominator by 1/2, 1/3, 1/4, 1/5, … until we get a sum of numbers that equals the numerator. In our first example, we would have 1/3 × 12 = 4 and 1/4 × 12 = 3, and since 4 + 3 is 7, we know that our unit fractions are 1/3 and 1/4. It is this last method that was used by the Egyptians to create fraction tables.

The fraction symbol was an eye, which meant that fractions could be written with the eye on top and the denominator written under the eye. For example, the following would be the way to represent 1/3:

The following are the special symbols for 1/2, 2/3, and 3/4, respectively:

While we are on the subject of eyes, the Egyptians had a symbol called the Eye of Horus, which was a symbol of protection and was represented by the goddess Wadjet, or “Whole One.” It was later associated with Horus, a god associated with the sun god Ra, who was depicted as a falcon. Each part of the eye was a unit fraction, and when taken together, they summed to 1. This is quite remarkable because even though the six unit fractions found in the eye, 1/2, 1/4, 1/8, 1/16, 1/32, and 1/64, did not really sum to 1, they came pretty close. In fact, if this series kept going it would truly be equal to 1. In other words, we would need 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 + 1/128 + 1/256 + · · ·. This series is called a geometric series, which means that the ratio of any two consecutive terms gives us a constant ratio. In this case, that constant ratio is 1/2. For example, 1/4 divided by 1/2 is 1/2, 1/8 divided by 1/4 is 1/2, and so on. Furthermore, this sum of an infinite geometric series is a/(1 – r), where a is the first term and r is the common ratio. In our example, we would have 1/2 divided by the quantity 1 minus 1/2, which yields 1/2 divided by 1/2 to give us 1. In Figure 2.1, we can find the first six terms in the eye. The right side of the sclera, or white of the eye, represents 1/2, the iris, or the color of the eye, and the pupil represent 1/4, the part of the eyebrow above the straight line coming out of the eye represents 1/8, the left side of the sclera represents 1/16, the curly part coming below the eye represents 1/32, and the thick straight part coming down from the eye represents 1/64.

FIGURE 2.1 Eye of Horus

The Egyptians also worked in geometry and were early in discovering the concept of area. They found the areas of typical mathematical shapes such as triangles and rectangles. The Egyptians had an interesting formula for finding the area of a circle, which they found by taking 8/9 of the diameter of the circle and then squaring this result. This closely compares with our own formula for the area of a circle: A = πr², where A is the area and r is the radius. π is the ratio of the circumference to the diameter of a circle. In other words, if we measure a circle to be one meter across (the diameter), then if we wrap a measuring tape around the circle, we would have approximately 3.14159 meters. If we consider the radius to be half the diameter, then we can turn the Egyptian formula into 16/9 of the radius, and then square that result. We use 16/9 instead of 8/9 since (8/9)d equals 8/9(2r), which equals 16/9 of the radius. Since 16/9 squared is 256/81, we can write the area as 256/81 multiplied by the radius squared. This means that the Egyptian value for π was 256/81, which is approximately 3.160493827. This calculation is very accurate for its time and close to the actual estimate: 3.1415926536.

The ancient Egyptians developed the world's first known unit of measurement, called the cubit. The cubit is a measurement of length and is a little longer than half a meter. It was based on the length of a person's forearm to the extended fingers. It consisted of seven palms, about the height of an extended fist, which also consisted of four digits or the four fingers in a fist. This means that there were 28 digits in a cubit. A measure of volume was the hekat, which was about 1.26 gallons, or 4.78 liters. The hekat was referenced in the two famous works that will be addressed next.

The ancient Egyptians recorded their writings on papyrus, a paper-like material derived from the papyrus plant. Two of the most famous papyri come from Egypt's Middle Kingdom Period, which spanned the time from around 2200 to 1800 BCE. The two famous papyri are the Rhind and Moscow Papyri. The Rhind Mathematical Papyrus, also known as the Ahmes Papyrus, is a copy of an earlier papyrus that dates to around 1600 BCE with the original at about 1800 BCE. It was acquired in 1864 by the British Museum from Henry Rhind, who had bought the Rhind Papyrus in Luxor in 1858, and the Brooklyn Museum has small fragments of the Rhind Papyrus today. The papyrus describes the work of the scribe Ahmes, the earliest known name in mathematics history. It had fraction tables to aid in calculation and 87 arithmetic and geometry problems, and it helps us understand the Egyptian method for multiplication. The Egyptian Mathematical Leather Roll, also acquired by Rhind, contains unit fraction sums. The smaller but older Moscow Mathematical Papyrus originated around 1800 BCE and was purchased by Vladimir Golenichev in the late 19th century in Luxor and contains 25 exercises in geometry. Today, it is housed in the Pushkin State Museum of Fine Arts in Moscow.

Before we close this chapter on ancient Egypt, we should address one of the most famous pharaohs in history, Ramesses II. The New Kingdom Period lasted from 1570 to 1070 BCE and was the time period of greatest wealth and power in ancient Egypt. This was the time of Tutankhamun, whose famous burial mask was found by Howard Carter in 1922. Thereafter, Ramesses II, who was born around 1300 BCE, reigned from 1279 BCE until his death in 1213 BCE. He is remembered for his great military victories and is considered to be the biblical pharaoh during the time of Moses and the Jewish Exodus from Egypt. Ramesses II had many wives but the best known was Nefertari. Ramesses II is the subject of the 19th-century CE English poem Ozymandias, written by Percy Bysshe Shelly. The poem reveals the story of a traveler who comes upon the decayed ruins of the statue of Ozymandias. On the base of the pedestal the traveler reads, “My name is Ozymandias, king of kings: Look upon my works, ye Mighty, and despair!” It is generally accepted to have a double meaning. The first meaning refers to the original intention of Ozymandias in his message to competitors, and the second refers to his message to the rulers of our time that all of their power and wealth would indeed be fleeting.

Next, we shall move on to the mathematics of ancient Mesopotamia with its center in Babylon. We shall see that the Babylonians had a system quite different from the Egyptians, but the system was just as remarkable.