

Table of Contents
Preface
Introduction
1 Truss Layout Optimization
1.1. Standard theory of mathematical programming
1.2. Governing equations of truss structures
1.3. Layout and topology optimization
1.4. Generalization
1.5. Truss geometry and topology optimization
1.6. Concluding remarks
2 Unified Formulation
2.1. Literature review
2.2. Disaggregation of equilibrium equations
2.3. Minimum volume problem
2.4. Minimum compliance problem
2.5. Reduced formulation for single loading
2.6. Nonlinear programming
2.7. Design settings
2.8. Concluding remarks
3 Stability Considerations
3.1. Literature review
3.2. Lower bound plastic design formulation
3.3. Nominal force method for local stability
3.4. Local buckling criterion
3.5. Formulation including stability constraints
3.6. Numerical examples
3.7. Concluding remarks
4 Structural Design Applications
4.1. Reticulated dome
4.2. Lateral bracing of Winter’s type column
4.3. Arch bridge
4.4. Suspension bridge
4.5. Dutch Maritime Museum
Conclusions and Future Prospects
Appendix
A1.1. Structural form-finding methods
A1.2. Metaheuristics for truss design
A1.3. Example of implementation
Bibliography
Index

First published 2014 in Great Britain and the United States by ISTE Ltd and John Wiley & Sons, Inc.
Apart from any fair dealing for the purposes of research or private study, or criticism or review, as permitted under the Copyright, Designs and Patents Act 1988, this publication may only be reproduced, stored or transmitted, in any form or by any means, with the prior permission in writing of the publishers, or in the case of reprographic reproduction in accordance with the terms and licenses issued by the CLA. Enquiries concerning reproduction outside these terms should be sent to the publishers at the undermentioned address:
ISTE Ltd
27-37 St George’s Road
London SW19 4EU
UK
www.iste.co.uk
John Wiley & Sons, Inc.
111 River Street
Hoboken, NJ 07030
USA
www.wiley.com
© ISTE Ltd 2014
The rights of Benoît Descamps to be identified as the author of this work have been asserted by him in accordance with the Copyright, Designs and Patents Act 1988.
Library of Congress Control Number: 2013957304
British Library Cataloguing-in-Publication Data
A CIP record for this book is available from the British Library
ISSN 2051-2481 (Print)
ISSN 2051-249X (Online)
ISBN 978-1-84821-674-7
Preface
Designing structures as light as possible is an intelligent and responsible way for engineers and architects to conceive structural systems. The key ingredient to achieve lightness relies on a thorough study of the structural form, which establishes a dialogue with forces. Nowadays, these structures are able to cross incredibly wide spans with the least amount of materials. Still, the quest for lightness must cope with current design constraints, which give sense to modern structures.
This book presents a computational method for the preliminary shape design of lightweight structures. The strategy relies on fundamental concepts of structural design to formulate an optimization problem combining the theories of mathematical programming and structural mechanics. The method considers many design settings including stress and displacement constraints, self-weight, multiple loading conditions and structural stability considerations. In addition, the conceptual framework is well suited to accommodate project-specific constraints. These building blocks result in an integrated design process at a midway between form finding and structural optimization. Several large-scale applications of three-dimensional bridge and dome structures emphasize the versatility and robustness of the proposed method.
This book is primarily written for graduate students and researchers in architectural, civil and mechanical engineering. It is also of significance for practioners in structural design who are concerned with the design of lightweight structures. Readers are assumed to have some basic knowledge of mathematical optimization and structural computational mechanics for a better understanding of this book.
Classical computational methods for designing lightweight structures are focused either on finding an equilibrium shape or are restricted to fairly small design applications. In this book, we aim to develop a general, robust and easy-to-use method that can handle many design parameters efficiently. These considerations have led to truss layout optimization, the goal of which is to find the best material distribution within a given design domain discretized by a grid of nodal points and connected by tentative bars.
Chapter 1 presents the general concepts of truss layout optimization, starting from topology optimization where structural component sizes and system connectivity are simultaneously optimized. The range of applications covers limit analysis and the identification of failure mechanisms in soils and masonries. To fully realize the potential of truss layout optimization for the design of lightweight structures, the consideration of geometrical variables is then introduced. The resulting truss geometry and topology optimization problem raises several fundamental and computational challenges, which are identified.
Then, Chapter 2 addresses truss geometry and topology optimization by combining mathematical programming and structural mechanics: the structural properties of the optimal solution are used for devising the novel formulation. To avoid singularities arising in optimal configurations, the present approach disaggregates the equilibrium equations and fully integrates their basic elements within the optimization formulation. The resulting tool incorporates elastic and plastic design, stress and displacement constraints, as well as self-weight and multiple loading.
In addition, the inherent slenderness of lightweight structures requires the study of stability issues. As a solution, Chapter 3 proposes a conceptually simple but efficient method to include local and nodal stability constraints in the formulation. Several numerical examples illustrate the impact of stability considerations on the optimal design.
Finally, the investigation of realistic design problems in Chapter 4 confirms the practical applicability of the proposed method. It is shown how we can generate a range of optimal designs by varying design settings. In this regard, the computational design method mostly requires the designer to have a good knowledge of structural design to provide an initial guess.
Benoît DESCAMPS
January 2014
Introduction
This introduction first describes lightweight structures in a historical context and points out current design issues. To tackle these challenges, section I.2 briefly discusses an empirical design process along with available methods for form finding and structural optimization. As a prelude to the novel method presented in this work, section I.3 introduces the conceptual framework of hanging models, plastic design and layout optimization leading to the computational design problem. The main achievements of the book are finally given in section I.4.
Structural design is an inseparable discipline of the art of building, whose governing factors are of a social, cultural, environmental, technical and financial nature. Given the considerable impact of the construction sector in terms of resources, today’s expectations are directed toward “meeting growing demand with limited resources”1. In this context, designing structures as light as possible may greatly contribute to more sustainability: by reducing the structural mass, we not only reduce the quantity of raw material, but we also decrease the embodied energy used for its production, transport, assembly, maintenance, and demolition or reuse, as well as the impact on the ground and foundations [KAN 07].
Lightweight structures are most suitable for covering wide spans with a limited amount of material. It is often argued that aesthetic values that make these structures visually appealing come from a functionally correct form, which mainly determines whether the system is able to withstand external loads without deteriorating serviceability, in addition to assessing the range of structural performance that can be attained. Mass and stiffness are the two fundamental criteria whose optimum is like systems of minimum energy in nature. To achieve the lowest mass-to-stiffness ratio, lightweight structures must be conceived as a force-differentiated system where tension, compression and shear are distributed on different components (cables, bars, membranes, etc.) [ERI 06]. If the structural form is inadequate, bending stiffness is required to compensate unbalanced forces, but this additional resistance adversely affects structural performance.
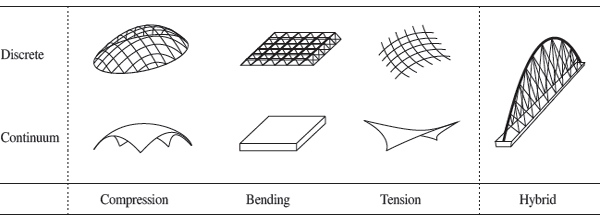
The emergence of lightweight structures can be traced back to the second half of the 19th Century. This period witnessed the advent of new material technologies such as steel, reinforced concrete, resistant glass and, later, fabric membrane. Together with advances in analysis and design tools, engineers and architects have been challenged to build increasingly lighter structures [LEW 03]. This has led to the development of the structural typologies depicted in Figure I.1. An early example was the Crystal Palace designed by Joseph Paxton for the Great Exhibition in London in 1851. The roof of 80 kg/m2 was a real progress at that time [KAW 11]. Another pioneering construction was the hyperboloid lattice tower by the Russian engineer Vladimir Shukhov in 1896. In the 1920s, Anton Tedesko first introduced reinforced concrete thin shells in the United States [HIN 04]. This expansion was pursued worldwide by Félix Candela [MOR 08], Heinz Isler [GAR 03] and André Paduart in Belgium [ESP 03]. The limit of lightness was achieved with tensile structures constructed of prestressed cable nets and fabric membranes; the strength coming from the anticlastic curvature of the geometric surface. A famous example of cable net is the roof of the Olympic stadium in Munich built in 1972, qualified as “architecture of the minimal” by its designer Frei Otto [OTT 96]. Pneumatic structures exhibit a close resemblance with tensile structures except that they are stabilized by the pressure of compressed air and prestressed cables. They also have an extremely low mass, as witnessed by the air-supported roof of 3 kg/m2 covering the US Pavillon at Expo’70.
Figure I.1. Classification of typologies of lightweight structures according to the actual stress state and the type of structural components
It should be mentioned that these historical examples were constructed in a period when labor was highly qualified and inexpensive, the requirements for safety and durability were more permissive, and when technical innovation gave meaning to the project. At the dawn of the 21st Century, a question arises: “the lighter, the better?” [KAW 11]. Although lightness remains the leading design criterion, this sole achievement is largely insufficient to cope with the increasing complexity of contemporary architecture. Nowadays, lightweight structures should be designed as a whole by including the multitude of design constraints. This will result in hybrid systems lying at the boundary of different typologies.
The shaping process for lightweight structures is traditionally based on empirical knowledge and designers’ experience. An initial design is created, tested and updated in a series of structural analyses in order to achieve an optimal shape (Figure I.2(a)). However, each iteration requires engineers to manually generate the geometry of the analysis model. The task is time-consuming, error-prone and cumbersome for the designer. Furthermore, no matter how brilliant the designer is, it is often difficult to accurately predict and comprehend the effects of changing the geometry of lightweight structures without the risk of deteriorating the stiffness. This trial-and-error process can be advantageously pushed forward by computational design methods.
Still, two fundamental issues of lightweight structures must be thoroughly addressed to benefit from these developments: equilibrium and optimality [DES 11a]. The search for equilibrium is the basic requirement for safety, but it may transform a satisfactory design into a masterpiece when it is properly considered. The search for optimality is the never-ending task of improving the design while satisfying project constraints. Over the last 40 years, researchers have been continuously devising innovative methods to address these issues.
Figure I.2. Different kinds of design process with a) the conventional trial-and-error process, b) the structural form-finding process and c) the structural optimization process

Finding an equilibrium shape is the main purpose of structural form-finding methods. Given the boundary and external loading conditions, this state-to-design approach requires the designer to prescribe the internal forces to obtain the geometrical coordinates that solve the equilibrium equations (Figure I.2(b)). The literature covering structural form finding is briefly discussed in Appendix A1.1. Although structural efficiency may result as a welcome side effect (no optimality criterion is used, in fact), there are frequent situations in which we wish to impose geometrical constraints. In this case, form-finding methods are inadequate since the shape is the output of the process. Furthermore, stability issues that may considerably affect the optimal shape cannot be considered. Some strategies have been proposed [ZHA 06b, DES 10, DES 11c, RIC 13, QUA 13], but their scope is restricted to specific problems.
Finding an optimal shape is the ambitious task of structural optimization. The approach requires the designer to mathematically formulate the structural design problem as an optimization problem consisting of the minimization of an objective function subject to inequality and equality constraints. In the classical design-to-state (or nested) approach, the design variables are introduced in a dedicated structural analysis routine which computes the state variables. Based on these responses, an optimization algorithm iteratively updates the design toward the optimum (Figure I.2(c)). As a rule for selecting an optimization algorithm, the more intensive the local exploitation, the stronger the need for specialized information about the problem to be optimized. Deterministic methods are problem-specific and best suited for local search (these aspects will be discussed later in this book), whereas metaheuristics (see the discussion in Appendix A1.2) have broader search capabilities. Structural optimization problems are often very large (several thousand variables and constraints) and the design space comprises many local optima. Hence, deterministic methods might produce small improvements if the problem is not properly stated, whereas metaheuristics might be inefficient if no variable selection has been applied a priori. Furthermore, the variable nature of the structural layout causes singularities during the optimization process [RIC 12, DES 13b].
Although structural optimization methods have tremendous potential, we have to accept that the promise of these approaches is not easily realized. These persisting problems prevent their routine use by structural designers. Instead, the widespread use of computer-aided design tools has enabled the development of increasingly complex geometries in freeform architecture. In this long-awaited freedom of design, structural considerations were perceived as restraining the creativity of designers. As a consequence, structural engineers have been excluded from the preliminary shape design process and their role has been recentered on sizing and checking arbitrarily defined structures to meet the standard code requirement. Against all odds, a handful of structural designers still pursue the line of thought for unity and coherence between form and force in architecture. Former theories on structural design can inspire the development of creative, yet rigorous, strategies to empower this momentum.
The design of lightweight structures relies on the catenary, whose mathematical definition is a hyperbolic cosine curve idealizing a hanging chain under its own weight when supported at its ends. The development of hanging-chain models started at the end of the 17th Century [KUR 08]. In a Royal Society Meeting, Robert Hooke raised the issue of finding the ideal shape for an arch and its thrust for which buttresses must resist. As a pioneering idea, he proposed today’s well-established approach of inverting the hanging-chain model to determine the equilibrium shape of an arch [HOO 75]. Soon after, Gregory extended Hooke’s idea by saying, without formal proof, that any other arch whose thickness encompasses a catenary curve is also stable [GRE 97]. The first rigorous calculation of the thrust line based on funicular polygon of graphic statics is attributed to Moseley [MOS 35] and Méry [MÉR 40].2 This (static) “equilibrium approach” was sparsely used in Europe until the Antoni Gaudí’s nature-inspired work applied the method in the chapel of Colònia Güell and the arches of Casa Milà [HUE 06].
During the 19th Century, the equilibrium approach was severely criticized by proponents of the elastic philosophy [HEY 99]. Classical elastic theory states that, in statically indeterminate structures made up of linear elastic material, among the infinity of statically admissible stress field, the actual state is obtained by enforcing the compatibility conditions between strains and displacements (continuity of elements, boundary conditions). However, experimental measures on masonry and steel frameworks3 exhibited discrepancies with elasticity theory. As claimed by Wilson [WIL 98], “equilibrium is essential, compatibility is optional” because compatibility is often violated, for instance in masonry due to cracks. Thus, plastic theory was born by the inability of elastic design theory to predict the actual stress state in a built structure.
Gregory’s statement about the stability of arches was in fact a precursor of plastic theory (or limit analysis). Assume a ductile material in the absence of elastic instability, any stress distribution enforcing static equilibrium equations without violating the yield condition is carried safely by the structure via plastic redistribution [HOR 50]. Together with the safe theorem, plastic theory replaces the problem of determining the actual stress distribution by a projected limit situation. The selection of an equilibrium state can be performed by adding the requirement that the solution should require the least amount of material (i.e. a lower bound solution). Hence, plastic theory is naturally oriented toward design [BUR 04].
In 1904 Michell stated a fundamental design principle of plastic theory [MIC 04]: given a design domain (Figure I.3(a)), the lightest structure satisfying the yield condition consists of a continuum with mutually orthogonal fields of tension/compression members oriented along principal strains (Figure I.3(b)). The analytical method to determine these lines assumes a fully stressed design in all load-carrying members. The displacement field must remain continuous throughout the design domain and satisfy the kinematic restrictions imposed on the solution [PIC 11]. Although the scope is essentially theoretical, the method is still being developed today [ZHO 04, DEW 09, SOK 10, ROZ 12] because (1) it provides the essential information about the limit of economy for a given structural frame and (2) it lays the basis of layout optimization.
Figure I.3. Michell’s half-wheel. The design domain is subjected to a central load and supported at both extremities a). The optimal solution is a semicircular arch with tension spokes carrying the load b)

4