
The Poincaré Conjecture

In Search of the Shape of the Universe
ALLEN LANE
an imprint of
PENGUIN BOOKS
ALLEN LANE
Published by the Penguin Group
Penguin Books Ltd, 80 Strand, London WC2R 0RL, England
Penguin Group (USA) Inc., 375 Hudson Street, New York, New York 10014, USA
Penguin Group (Canada), 90 Eglinton Avenue East, Suite 700, Toronto, Ontario, Canada M4P 2Y3
(a division of Pearson Penguin Canada Inc.)
Penguin Ireland, 25 St Stephen’s Green, Dublin 2, Ireland (a division of Penguin Books Ltd)
Penguin Group (Australia), 250 Camberwell Road,
Camberwell, Victoria 3124, Australia (a division of Pearson Australia Group Pty Ltd)
Penguin Books India Pvt Ltd, 11 Community Centre,
Panchsheel Park, New Delhi – 110 017, India
Penguin Group (NZ), 67 Apollo Drive, Rosedale, North Shore 0632, New Zealand
(a division of Pearson New Zealand Ltd)
Penguin Books (South Africa) (Pty) Ltd, 24 Sturdee Avenue,
Rosebank, Johannesburg 2196, South Africa
Penguin Books Ltd, Registered Offices: 80 Strand, London WC2R 0RL, England
www.penguin.com
First published in the United States of America by Walker Publishing Company, Inc. 2007
First published in Great Britain by Allen Lane 2007
Copyright © Donal O’Shea, 2007
The moral right of the author has been asserted
All rights reserved
Without limiting the rights under copyright
reserved above, no part of this publication may be
reproduced, stored in or introduced into a retrieval system,
or transmitted, in any form or by any means (electronic, mechanical,
photocopying, recording or otherwise), without the prior
written permission of both the copyright owner and
the above publisher of this book
A CIP catalogue record for this book is available from the British Library
EISBN: 978–0–141–90034–6
Preface
1. Cambridge, April 2003
2. The Shape of the Earth
3. Possible Worlds
4. The Shape of the Universe
5. Euclid’s Geometry
6. The Non-Euclideans
7. Bernhard Riemann’s Probationary Lecture
8. Riemann’s Legacy
9. Klein and Poincaré
10. Poincaré’s Topological Papers
11. The Great Savants
12. The Conjecture Takes Hold
13. Higher Dimensions
14. A Solution in the New Millennium
15. Madrid, August 2006
Notes
Glossary of Terms
Glossary of Names
Timeline
Bibliography
Further Reading
Art Credits
Acknowledgments
Index
To Mary and my parents
This book is about a single problem. Formulated by a brilliant French mathematician, Henri Poincaré, over one hundred years ago, the problem has fascinated and vexed mathematicians ever since. It has, very recently, been solved. The Poincaré conjecture addresses objects that are central to our understanding of ourselves and the universe in which we live.
I write for the curious individual who remembers a little high school geometry, but not much more—although I hope that those with substantial mathematical backgrounds will also enjoy the book. Endnotes are addressed to those who know more, or who want to know more.
Go to any gathering. Sit beside anyone in a plane. And listen to what they say about mathematics. A few love it. But more do not, and what they say is not pretty. Some believe themselves congenitally incapable of mastering it. Some dislike it. And many loathe it with the passion reserved for love gone bad.
How can one subject, filled with so much beauty, inspire such a range of responses? The aversion some people feel seems to be rooted in fear. I have no illusions that one book will change this. But if you are a reader with ambivalent feelings toward mathematics, I hope this book inspires you to read further or, if you are a student or someone contemplating further study, to consider taking more mathematics courses.
I hope that you enjoy reading what follows as much as I enjoyed writing it.
Revolutions in mathematics are quiet affairs. No clashing armies and no guns. Brief news stories far from the front page. Unprepossessing. Just like the raw damp Monday afternoon of April 7, 2003, in Cambridge, Massachusetts.
Young and old crowded the lecture theater at the Massachusetts Institute of Technology (MIT). They sat on the floor and in the aisles, and stood at the back. The speaker, Russian mathematician Grigory Perelman, wore a rumpled dark suit and sneakers, and paced while he was introduced. Bearded and balding, with thick eyebrows and intense dark eyes, he tested the microphone and started hesitantly: “I’m not good at talking linearly, so I intend to sacrifice clarity for liveliness.” Amusement rippled through the audience, and the lecture began. He picked up a huge piece of white chalk, and wrote out a short, twenty-year-old mathematical equation.1 The equation, called the Ricci flow equation, treats the curvature of space as if it were an exotic type of heat, akin to molten lava, flowing from more highly curved regions and seeking to spread itself out over regions with lesser curvature.
Perelman invited the audience to imagine our universe as an element in the gigantic abstract mathematical set of all possible universes. He reinterpreted the equation as describing these potential universes moving as if they were drops of water running down enormous hills within a giant landscape. As each element moves, the curvature varies within the universe it represents and it approaches fixed values in some regions. In most cases, the universes develop nice geometries, some the standard Euclidean geometry we studied in school, some very different. But certain tracks that lead downhill bring problems—the elements moving along them develop mathematically malignant regions that pinch off, or worse. No matter, the speaker asserted, we can divert such tracks; and he sketched how.
The audience had been drawn to the lecture by a paper Perelman posted to a Web site the previous November. In the paper’s final section, he’d outlined an argument that, if valid, would prove one of the most famous, most elusive, and most beautiful conjectures in all of mathematics. Posed in 1904 by Henri Poincaré, the leading mathematician of his era and among the most gifted of all time, the Poincaré conjecture is a bold guess about nothing less than the potential shape of our own universe. But it is a guess, nonetheless. The challenge of proving or disproving it has exerted a sirenlike pull on mathematicians and has made it the most famous problem in not only geometry and topology but arguably in all of mathematics.2 In May 2000, the Clay Institute, an institute dedicated to the advancement and dissemination of mathematical knowledge, had designated the problem as one of seven millennium problems and offered a million-dollar reward for its solution.3
Well over half the audience would have tried to make some headway on the Poincaré conjecture. Every person in the room—from the preppy-looking thirty-something-year-old with spiked hair, taking notes in Chinese, and the young blonde with the tight blouse and the too-short skirt, to the jogger in baggy running shorts and damp T-shirt, and the rheumy-eyed octogenarian with herringbone coat stained by decades of chalk dust—knew that they were potentially witnessing a monumental milestone in a three-thousand-year-old legacy. The mathematics invoked had been passed painstakingly from one era to another, through times of great wealth and times of shattering poverty, from the unknown Babylonian who gave us the area of a circle, to the perfect severities of Euclid, to the blossoming of geometry and topology over the last two centuries.
Two weeks and several lectures later, at the flagship campus in Stony Brook of the State University of New York a similar scene ensued. That lecture theater was even more crowded. This time, several reporters were in the room. The reporters had heard that Perelman had made a stunning discovery relating to the shape of our universe, and that he might win a million-dollar prize as a result. They had also heard of his shadowy career path—how he dropped out of sight a decade earlier, his brilliance recognized and his promise unrealized. A light-bulb flashed. “Don’t do that,” Perelman snapped, visibly annoyed.
The mathematician patiently answered all questions from the audience after his lecture. Those questions came furiously. “But that solution will blow up in finite time,” came a voice from the middle of the room. “It doesn’t matter,” replied Perelman; “we can cut it out and restart the flow.” Silence, then a couple of nods. The listeners were cautious, weighing what they heard. They would have to ponder his words for months to come, but this sounded promising.
Much of the mathematics Perelman called upon would have been inconceivable three decades previously. The technical tools that he used were at the very edge of what was possible and depended critically on the work of a number of persons in the audience. The atmosphere was tense. Everyone knew how delicate and how subtle the speaker’s arguments were, and how easy it was to go astray. Everyone wanted them to hold. A Web site had sprung up,4 managed by two professors, Bruce Kleiner and John Lott, in the University of Michigan’s extraordinary mathematics department. The site contained links to Perelman’s papers. Mathematicians around the world had added remarks and arguments clarifying obscure points and expanding on passages that seemed too terse.
Almost every mathematician, geometer or not, knew someone at the lecture and was waiting for an account. Most of the audience took notes, for their own benefit and for friends. Two, Christina Sormani, a young professor at Lehmann College, and Yair Minsky, then a freshly minted full-professor at Yale, would post their notes on the Web site, so that others would have access.
As at MIT, everyone in the room, young and old, except the reporters, realized that what they were hearing was the culmination of over a century of the greatest flowering of mathematical thought in our species’ history. The lecture demanded close attention, leaving little space for stray thoughts. Even so, many would have thought of an especially cherished event or paper, recent or long past, that relates to Poincaré’s work or of a person, possibly long dead, who would have loved to have heard this talk. All delighted in the wealth of good ideas and the promising paths to be explored.
The reporters, on the other hand, wanted to know about the million dollars. How did Perelman feel about the possibility of winning that kind of money? As it dawned on them that he did not care, they changed their approach and wrote stories about a reclusive Russian making a big math discovery, and speculated that he would reject the prize. Perelman filled in more details on subsequent days and during hastily organized discussion sessions. But he refused all interviews with journalists and returned to Saint Petersburg a few weeks later without responding to the job offers proffered by top American universities.
The Poincaré conjecture and Perelman’s proof of it is one of the greatest achievements of our age; it tells us much about the possible nature and shape of our universe. The Ricci-flow equation Perelman wrote, a type of heat equation, is a distant relative of the Black-Scholes equation that bond traders around the world use to price stock and bond options. But curvature is more complicated than temperature or money. As subsequent chapters will explain, curvature is a geometric object that requires more than one number to describe it, and the Ricci-flow equation that Perelman uses is shorthand for six linked equations, a triumph of elegance, simple to behold and concealing dazzling riches. Its closest analogue is the Einstein equation of general relativity that expresses the curvature of space-time.
The Poincaré Conjecture tells the story of the mathematics behind the conjecture and its proof. To speak of mathematics sensibly is to speak not just of results, but of the people who brought those results to pass. To the extent that mathematical achievement enters popular consciousness at all, it often reflects the romantic myth of a solitary genius heroically wresting understanding from an uncaring cosmos. There are indeed individuals whose insights seem to come from nowhere and who have single-handedly moved the discipline decades ahead. But, as colorful and as mysterious as genius is, mathematical progress also depends on thousands of other individuals, and on the institutions and societies in which they work and live. It is past time to tell this larger story. The narrative ranges from Babylon of five thousand years ago to present-day Saint Petersburg, northern New York State, and Madrid. It tells of exploration, war, scientific societies, and the emergence of the research university in Germany and most recently in the United States—tracing the history of geometry, the discovery of non-Euclidean geometry, and the birth of topology and differential geometry through five millennia, dozens of societies and human institutions, and hundreds of individuals.
Mathematical exposition has been interwoven with biographical, cultural, and historical material. There will be too much mathematics for some and far too little for others, but most people with a high school education will be able to follow the basic concepts of this book, even if the finer points are a bit challenging. One can understand and appreciate the mathematics and this famous conjecture without being able to “do the math” oneself. For the convenience of readers, a glossary of mathematical terms, an index of persons, and a list of major events detailed in the narrative follow the endnotes.
Some of the mathematics originated deep in the past, millennia ago. Mathematical investigation is one of the oldest human activities, as old as the trades of carpentry, cookery, and metal-working. But in fact, more mathematics has been discovered since 1900 than in all previous human history. As a result, the pace picks up and the reliance on endnotes for details and references becomes more advanced as the narrative advances closer to the present. Lightly skim the more mathematical sections and notes. There is no test. You can always return later, if you wish, to puzzle out whatever seems unclear. After all, Poincaré’s conjecture has stumped the most learned mathematicians for the last hundred years.
The Poincaré conjecture provides conceptual and mathematical tools to think about the possible shape of the universe. But let us start with the simpler question of the shape of our Earth. Any schoolchild will say that the Earth is round, shaped like a sphere. And, in these days of airplanes and orbiting spacecraft that can take pictures of our planet from on high, this seems utterly obvious. But, in times past, it was difficult to say with certainty what the shape of the world was.
“Is there anyone so foolish as to believe that there are persons on the other side of the earth with their feet opposite to ours: people who walk with their heels upward and their heads hanging down?” According to Washington Irving, mid-nineteenth-century America’s celebrated public intellectual, this rhetorical question of an early Christian Church father was among those cited by the advisory committee convened by King Ferdinand and Queen Isabella to evaluate Christopher Columbus’s proposal to sail west to the East Indies.5 Irving breathlessly recounts how the skeptical, even hostile, committee members, blinded by their belief in a flat Earth, repeatedly challenged Columbus.6 Alone before the learned committee, in the land of the Inquisition, Columbus steadfastly defended his views.
Irving’s portrait of Columbus has endured and has been retold uncritically by generations, but it is nonsense—“pure moonshine,” wrote the highly respected American historian Samuel Eliot Morison.7
In 1490, virtually every educated Westerner believed that the Earth was spherical. There were, to be sure, debates about the existence of antipodeans, persons who lived on the other side of the world and who could not have known Christ or the Prophet. In the absence of knowledge, fantasy flourished. There were widely believed tales of huge areas with fearsome storms that made passage impossible. Horrific depictions of monsters abounded. Some argued that the other side was a great sea with no land and no antipodeans.
Columbus and the advisors to Ferdinand and Isabella did disagree, but their disagreement was about the size of the Earth, not its shape. All of them believed that the world was spherical. However, although there were some very good, detailed maps of parts of the Earth (notably the Mediterranean basin), and assemblages of these maps into atlases, no one really had any idea of the distance around the world. The most authoritative estimates had come from the ancient Greeks. In the second century, Ptolemy estimated the circumference as 18,000 miles. The court advisors of the Spanish monarchs favored the estimate of the Erastosthenes, a Greek geometer of the third century BCE: He had given the circumference a value of 24,200 miles, very close to today’s value of 24,902 miles. Columbus argued that the Earth was even smaller than Ptolemy thought. The advisors, not Columbus, were right. Had their views prevailed, Columbus would not have received the financial support he needed, because the cost of outfitting an expedition for the longer voyage and the increased risk would have been prohibitive.
Columbus’s reputation has risen and fallen over time. He was hailed initially for his wisdom, his courage, his vision, even his looks. The five-hundredth anniversary of his voyage brought some different, darker assessments: Columbus as rapacious imperialist, headstrong, the beneficiary of blind luck. The explorer was indeed lucky that the Americas were where they were. However, he was acting on the best information then available. He had heard of rumors of the Norse voyages and those of the Irish navigator, Brendan. If they had reached Asia, as it then seemed reasonable to suppose, then Erastosthenes and Ptolemy both had to be wrong. This was certainly more reasonable than supposing there was an undiscovered continent between Europe and Asia: there were abundant instances of data upon which Ptolemy relied having been erroneous.
To his death, Columbus believed that he had reached the Spice Islands to the east of India. He knew that it took far longer to get to them by sailing around Africa and he struggled to reconcile this with his own observations. He writes: “I find that the earth is not as round as it is described, but it is shaped like a pear, which is round everywhere except near the stalk where it projects strongly; or it is like a very round ball with something like a woman’s nipple in one place, and this projecting part is highest and nearest heaven.”
This passage has often been ridiculed, but I find it quite inspiring.8 Here we have an old man, who has believed and argued all his life that the Earth is a perfectly round sphere, still open to other hypotheses that better fit the data. Perhaps, he is arguing, the Northern Hemisphere is like a small narrow stalk and the Southern Hemisphere bulges like the bottom of the pear. Maybe we can reach the Spice Islands relatively quickly by sailing around the narrow neck of the Northern Hemisphere, whereas to sail around Africa in the larger Southern Hemisphere to get to them results in having to travel much further. The willingness to reexamine lifelong beliefs because of conflicting data takes enormous courage, and contrasts sharply with recent examples of public discourse in which our political, cultural, and religious leaders have fit data to preconceived theories.
Arguments about the circumference of the Earth aside, the fact is that no one in 1490 really knew whether the Earth was finite, much less a sphere. About the only thing known for certain was that the Earth was curved, and large regions had been mapped. Where, then, did the belief that the world was a sphere arise, and how did it gain such wide acceptance?
The story of how the Earth was first understood to be spherical begins about two thousand years before Columbus’s voyage, on the Greek island of Samos. In Columbus’s time, Samos was almost entirely depopulated. Its location a mile off Turkey’s western coast had made it a target of every possible invader: Byzantines, Arabs, Venetians, Crusaders, Turks. Even today, the quiet towns, the white sand beaches, the olive trees and the vineyards along the road circling the Karvounis or Kerkis mountains, suggest nothing so much as warm indolence and ageless torpor. But drive or cycle eight miles south of the present-day town of Samos and one will come to the town of Pythagoreion. Named for Pythagoras, Samos’s most famous citizen, it sits on the partially buried ancient city of Samos. Take the left fork in the road and continue along the seashore. Over a rise is a valley and the ruins of the Heraion, the temple of Hera, one of the seven wonders of the ancient world. A single column, half its original height, stands on a massive stone foundation, all that remains of the 155 columns that once graced this place. Nearby is the Evpalinos aqueduct-tunnel, now strung with lights and open to the public. The sense of grandeur past overpowers the pallid present.
Continuing another 20 miles from the ruins of the temple along the main road brings the hilltop town of Marathokampos into view to the west. A small sign there marks a hiking trail up Mount Kerkis and to a cave where Pythagoras taught. A moderately strenuous ascent leads to a shaded grotto and a spacious cave. Walk down a bit, and the rocky slope of Kerkis and the impossibly blue Aegean Sea stretch out far below. The remoteness, the beauty, and the solitude call to mind Ireland’s Skellig Rock or the eastern slope of the sacred volcano Haleakala on the Hawaiian island of Maui. At such places, the present thins and the past seems close. Ancestral voices murmur just below the threshold of hearing. It is here that Pythagoras first taught that the Earth was a sphere. His spirit is still here, the locals say. On dark nights when the winds scour the face of Kerkis, they tell of the faint light that shines out from the rocks guiding mariners far below.
That light burned brightest twenty-five hundred years ago in the heyday of Samos, then an important city-state of Ionia. This small region consisted of the westernmost coast of Turkey, or Asia Minor, extending from Phocaea south about a hundred miles to Miletus, together with the islands in the Aegean just off the mainland. Oral tradition maintains that the Greeks had colonized the region at the beginning of the first millennium BCE. Here, the Greek economy and culture rebounded after the so-called Dark Age, the period of nearly five hundred years of depopulation, economic hardship, and the loss of literacy following the violent and still mysterious destruction of the Mycenaen civilization in the twelfth century BCE.
The work of the Ionians Homer and Hesiod marked the beginning of a renaissance. Writing, based on the alphabet from Phoenicia (present-day Lebanon) was introduced in the late ninth century BCE and promptly used to write down Homer’s epics. Between the seventh and fifth centuries BCE, Samos became a great naval power, and the mainland Ionian city-states important and powerful trading centers. Greek philosophy and science emerged in Ionia at the same time.
Ionia’s location on the fringes of Asia Minor meant that Ionian thinkers had contact with the other great civilizations of the eastern Mediterranean, particularly Egypt. Far to the east was the legendary Babylon and, further still,
FIGURE 1. Ionia
Persia. The great Ionian philosophers Thales (624–547 BCE) and Anaximander (611–545 BCE), both of Miletus, taught that the cosmos and the motions of the stars were governed by laws of nature, not magic or the arbitrary intervention of divine beings. The cosmos was ordered and could be understood through reason and logical thought. This was a new idea, one that would take a while to catch hold, and one whose influence would wax and wane in different times and places.
Thales and Anaximander also speculated on the shape of the Earth. Thales had adopted the Egyptian belief that it rose like a hill from a smooth, presumably infinite, sea. Anaximander, who had given the matter a little more thought, believed that the Earth was shaped like a cylinder and suspended in space.
Pythagoras (569–475 BCE) had a much larger appetite for religion and mystery than did the Ionian philosphers. His father, Mnesarchus, a trader from the wealthy city-state of Tyre, moved from Phoenicia to Ionia, where he met and married Pythais of Samos. According to one story, Mnesarchus was granted citizenship on Samos after having brought grain to the island during a time of famine. Pythagoras traveled widely with his father, meeting Syrian and Chaldean scholars on a trip back to Tyre, and journeying to Italy and
FIGURE 2. Ionia, Egypt, and the East
Greece. He was something of a prodigy and displayed an early interest in philosophy that was nurtured by his teacher, Pherekydes (c. 600–550 BCE), and by Thales and Anaximander. Thales made an especially strong impression; famous and respected throughout Ionia, he was an old man when he met Pythagoras. Thales had spent time in Egypt in his youth and it was he, fatefully, who encouraged Pythagoras to do the same.9
In Egypt, Pythagoras somehow managed to become initiated into the sacred Egyptian mysteries. Just how a foreigner was allowed to learn the highly secret rites is unclear. All sources agree, however, that he had a striking golden birthmark on his leg, which suggests, perhaps, that the Egyptian priests believed him to be favored by their god Osiris and thus allowed him to join their priesthood. Certainly, there were widespread rumors later in Pythagoras’s life that he was partly divine and had been touched by Osiris, rumors that he appears to have done little to discourage. Details of his years in Egypt are even more muddled than those of the rest of his life. He seems to have been captured, presumably in the Persian invasion of Egypt in 525 BCE, and taken as a prisoner from Egypt to far off Babylon, 55 miles from present-day Baghdad and then the richest city in the world. There he learned the mysteries of Persian dualism, absorbing the teachings of Zarathustra (known to the Greeks as Zoroaster). Pythagoras must also have learned much of his mathematics in Babylon. Babylonian mathematics was much further advanced than Egyptian mathematics (which had come from Babylonia) and, although there is a fair amount of debate about how much mathematics Thales knew, Pythagoras knew much more and attained a much higher level.10
The circumstances of Pythagoras’s release from Babylon are lost, but his return to Samos did not go unreported. A striking figure in his Eastern trousers and garb, worn to conceal the birthmark, and a spell-binding orator, he was a sensation. His teachings thoroughly interwove the rational and irrational, the scientific and the mystical, and provided a marked contrast to the sobriety of the Ionian philosophical school. Their power still inhabits the abandoned surrounds of his cave on Samos.
Around 530 BCE, Pythagoras and a number of followers moved to Croton, a quiet Greek colony in the south of Italy that had been founded nearly two centuries earlier and may have been the center of a religious revival that was sweeping the region. There, Pythagoras founded his school. Actually, it was less a school than a brotherhood, itself a misnomer as this association of like-minded truth-seekers also admitted women. Called “the semicircle,” it had an inner group of men and women, the mathematikoi, strict vegetarians who lived communally, did without personal possessions, and were taught by the great man himself; and an outer group, the akousmatics, who lived in their own houses under much less stringent rules. Members underwent elaborate initiation rites and were sworn to secrecy.
The Pythagoreans believed that, at its deepest level, reality is mathematical, that all beings are related, that philosophy can be used as a means for spiritual purification, and that the soul can rise to union with the divine. The attractiveness of their notion of universal relatedness and the exotic blend of Eastern mysticism and Greek thought fascinated their contemporaries. Pythagoras and the Pythagoreans flourished, and became known throughout the Greek world. Time has softened the debates that raged about Pythagoras’s character and stilled the legends that swirled about the man. He was a riveting speaker, alleged to have remembered details from previous incarnations. To admirers, he was a genius with extraordinarily deep knowledge, wise and compassionate beyond measure. To detractors, he was a charlatan with an unerring instinct for self-promotion. Whatever the truth, Pythagoras was enormously influential, and the prestige of his brotherhood actually increased after his death.
Most important, Pythagoras had taught that the Earth was spherical. He had begun to accumulate evidence to support this idea, and had been the first to conceive of the Earth as existing together with the stars in a single universe. Later Pythagoreans, notably Philolaus (c. 470–385 BCE), even relinquished the notion of a geocentric universe, teaching instead that the Earth, Sun, and stars orbited an unseen central fire.
So now we know when and where the notion that the surface of the Earth was a sphere originated. If the Pythagoreans were sworn to secrecy, how did their knowledge leak out? And once it did, why was it taken seriously and how did it get transmitted to modern times?
The first thing to realize is human nature has changed little over three millennia. Mystery attracts us, and few resist the allure of great knowledge secretly held. Witness the success of recent novel and film The Da Vinci Code. The visibility of the Pythagoreans guaranteed a market for books purporting to expose their concepts and beliefs. And lots appeared. Philolaus allegedly wrote his book On Nature because he needed money.
The great philosopher Plato (427–347 BCE) would be much influenced by the Pythagoreans. He purchased Philolaus’s book for the Academy, the school he founded in Athens. He also had been a very close friend of the first-rate Pythagorean mathematician, Archytas (c. 428–350 BCE). As a result, many Pythagorean ideas made their way into Plato’s system and the mainstream of Greek thought. The Academy’s most brilliant student, Aristotle (384–322 BCE), though less enamored of the Pythagoreans (he is reputed to have dismissed them as “filthy vegetarians”), incorporated many of their ideas into his own formidable body of work.
The importance of Aristotle is difficult to overstate, for his intellectual reach was enormous. He codified the rules of formal logic, systematized philosophy, and contributed to all of the natural sciences. He taught that the Earth was a sphere around which the Sun and Moon rotated. His works on ethics, aesthetics, and politics are still read today. Medieval thought, both Christian and Islamic, is rooted in Aristotelian principles. Backed by the authority of Plato and Aristotle, and by discoveries that I shall describe momentarily, the notion that the earth was spherical took firm hold.
Aristotle’s role as private tutor of Alexander the Great,11 then the most powerful man in the world, served to propagate Pythagorean ideas even more decisively, albeit less straightforwardly, than his direct teachings. Alexander had built on his father’s conquest of Greece in 338 BCE and had gone on to conquer the then-known world. By the time of his death in 323, Alexander’s empire extended from around the Mediterranean into India.
Although the complexities of the relationship between the tutor and his gifted student are forever lost, Aristotle doubtless importuned Alexander to use his campaigns for scientific observation. Whether on account of this intercession or not, Alexander took mapmakers on his campaigns. Their maps did not survive, but the writing of some of his generals did, and their descriptions and accounts became the basis of maps created centuries later.
After Alexander’s death, his empire fell apart. The largest share fell to his general, Ptolemy Soter I, who chose as his capital Alexandria at the mouth of the Nile. Here, in the first, and the greatest, of the eponymous cities commissioned by Alexander the Great, Ptolemy began the construction of the fabled library that would secure Alexandria’s position as the intellectual and cultural capital of the world. Scholars flocked to the great library, eager to do research in a collection that held hundreds of thousands of books and scrolls. The position of head librarian was perhaps the highest academic position that one could hold in the ancient world, easily rivaling the headship of Plato’s Academy in Athens and akin to the presidency of Harvard University or mastership of Trinity College today.
Eratosthenes (275–195 BCE) of Cyrene (now Shahhat in Libya) became the third head librarian in 235 BCE in the reign of Ptolemy II. A geographer who had studied in Athens, Eratosthenes also wrote poetry and literary criticism, and pursued work in mathematics, astronomy, and philosophy. He had no doubt that our world is a sphere—if one were to sail west from Spain, he wrote, one would eventually encounter India. He even made a map of it.
Most famously, he noted that two individuals many miles apart, one directly north of the other, will see the Sun at different angle at the same time of the day, and pointed out that if one assumed that the world was a sphere, one could use the differences in the angles to estimate the distance around the world. Eratosthenes measured the difference between the angles between the Sun at noon at Alexandria and at what is now Aswan, 486 miles south on the Nile, and produced the stunningly accurate estimate12 of the circumference of the Earth championed by some of Columbus’s detractors at the Spanish court. A few generations later, Hipparchus (190–120 BCE), proposed that the Earth circled the Sun, and established measurement by latitude and longitude, dividing the world into 360 degrees.
Alexandria continued to be home to geographers, mathematicians, and astronomers long after the great library was destroyed.13 The greatest of these was Claudius Ptolemy (85–165 CE). His Geography was a category killer: a book that collated all previous knowledge, that was utterly authoritative, and that became the absolute standard. Ptolemy discussed the problem of mapping a curved earth onto a flat piece of paper and of dealing with the possible projections of a sphere to a plane. He pointed out that once one has associated coordinates (in this case latitude and longitude) with places being mapped, one can reconstruct a map at will. Using the surviving writings of Alexander’s generals and data acquired by other travelers, Ptolemy calculated the latitude and longitude of all known places.
The maps included in the original edition of Ptolemy’s Geography have been lost. However, that barely matters. The text is absolutely lucid and can be read with profit even today.14 Overall, Ptolemy imagined that the habitable portion of the Earth, from the coast of Western Europe to India and beyond, was about half of the entire planet. He estimated the circumference of Earth at 18,000 miles, considerably less than the value given by Eratosthenes, but greater than that of Columbus.
Ptolemy’s Geography was largely forgotten for many years, except by a number of Muslim scientists. In Palermo, in the multicultural court of the Norman King Roger II, al-Idrisi (c. 1100–1165) used an Arabic translation of the great work and improved on Ptolemy’s calculations. The Greek text was lost and not rediscovered until a Byzantine monk, Maximos Planudes (c. 1260–1330), found a manuscript copy without the maps. Planudes reconstructed some maps and commissioned the re-creation of others. In 1406, the text was translated into Latin, and a Benedictine monk, Nicolas Germanus, redrew the maps on a trapezoidal projection, one of the three proposed by Ptolemy.15 This became the basis of the first printed Ptolemy atlas, which was published in Bologna in 1477 in an edition with five hundred copies. Columbus owned a copy and studied it carefully.
The transmission of Pythagoras’s view, via Plato, Aristotle, the learned geographers of Alexandria, Sicily, and the early medieval world, had been successful. By the time of Columbus, virtually everyone believed that the Earth was spherical. The preponderance of the evidence supported this belief. If one looked at the Sun from different places on a north–south line, one saw it at different angles. When a ship sailed into sight from a long distance off, one could first make out its mast, then the rest of the ship. The tides, night and day, the phases of the Moon, and many other natural phenomena could be more reasonably understood by thinking of the Earth as a sphere.
Belief is one thing, but when did we really know, without any doubt, that the world was shaped like a sphere? We have seen that Columbus began to doubt the sphere theory, thinking of the Earth as pear shaped. And today we know that our planet is not a perfectly round sphere, but is flattened somewhat at the poles. But, as we shall see presently, there are other more radical possibilities: the question of the Earth’s shape is much more than a matter of bumpiness and flattened regions.
Our certain knowledge of the world’s shape had to await exploration and careful mapping of all regions. The two centuries following Columbus saw the production of ever more extensive atlases of the Earth. These have been among the most prized and sought-after books of all time. The Ptolemy atlas that Columbus had used was republished in Rome in 1508 by Berandus Ventus de Vitalibus. This was the first edition to include the European voyages to the new world, and around the Cape of Good Hope. The world map included a small America.
Jacobus Pentus de Leucho, of Venice, republished Ptolemy as Liber Geographicae in 1511, with twenty-eight maps and the text carefully edited by Bernardus Sykvanus, of Eboli. Abraham Ortelius, geographer to King Philip II of Spain, published his Theatrum Orbis Terrarum in 1570. It was to go through many editions, but there were large blank spaces where nothing was known, and the scales were wildly inaccurate.
Ortelius’s friend, Gerhard Mercator, of Rupelmonde, a Belgian and the greatest geographer since Ptolemy, revolutionized mapmaking by introducing a map projection (now known as the Mercator projection) that allowed mariners to plot constant bearing courses. Atlases based on his work and the continuing expeditions of European explorers began to appear at the end of the sixteenth century in Amsterdam. In fact, the word atlas referring to a collection of maps comes from Mercator’s practice of prefacing his map collections with a picture of the Greek god Atlas, shown supporting the world on his shoulders.
The most expensive, and the most celebrated, printed book of the seventeenth century was Joan Blaue’s multivolume Atlas Major, which was published in four languages in 1662–63. Stunningly beautiful, it nonetheless contained many inaccuracies (some unforgivable, even at that time) and gaps.
Although it seemed highly unlikely that the world went on forever or, worse, came to an end, we did not know for certain that neither hypothesis was true until the return in 1522 of Magellan’s expedition around the world.16 And even after Magellan, it was not completely clear that the Earth was a sphere. Other possibilities existed.
This may seem ridiculous. But is it? The extraordinary world map created by Battista Agnese in 1546 depicts Magellan’s voyages. Agnese clearly thought the world was spherical. And in looking at this map today, we tacitly think of all points on the top edge as going to a single point (the North Pole), and all on the bottom edge as being identified with a single, different point (the South Pole). Moreover, each point on the right edge corresponds to a point on the left edge with the same latitude. Modern observers know that this is the “right” way to interpret this map, and others like it, because people have explored the world and know which areas are continuous lands or bodies of water. But in Agnese’s time, with such large territories unmapped, it was conceivable that one might go off the north (that is, top) edge of the map and come back in the south (that is, bottom) edge of it. Or that maybe one could go north (or south) forever and never come back.
FIGURE 3. Agnese’s map
FIGURE 4. Atlas of an Imaginary world
Consider, for example, figure 4, the atlas of an imaginary world that does not appear at first sight too different from ours. The maps do not fit together on a sphere!
To understand the world covered by these maps, connect the maps together by overlapping the eastern (rightmost) part of each map to the western (leftmost) part of the map on the right. Likewise, overlap the north (top) part of each map with south (bottom) part of the map immediately above it. So far so good. We thereby obtain the map of the world shown in figure 5.
Now, the places depicted on the right edge of the map are the same as those on the left edge. Again, so far so good. This is just like what we are used to. But we are also accustomed to assuming that all points on the top part of the map are a single point, the North Pole. Look closely. This is not the case here. Indeed, every point along the top edge is the same as a point at that same longitude along the bottom edge, but the points at different longitudes on the top edge are different.
To get a representation of this world in space, a globe so to speak, we have to glue the right edge to the left edge and the top edge to the bottom edge. What do we get? Now, as a schematic, figure 6, shows, when we glue the top
FIGURE 5. Gluing the maps to make a world map
edge of a rectangle to the bottom we get a cylinder. Gluing together the right and left edges amounts to attaching the right and left circles of the cylinder, which gives the surface of a doughnut. Such a surface is called a torus (to distinguish it from the solid thing that we eat).
One might object that there is no way that our world could look like a torus. If one lived on the surface of the inner ring (facing the hole in the doughnut), wouldn’t one see the part of the surface opposite rapidly rising off into space? Maybe. But what if the world were enormous? Or what if the part
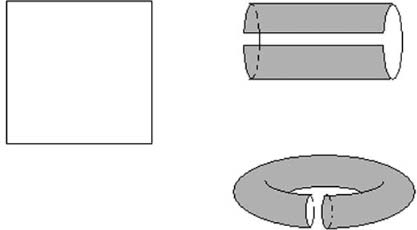
FIGURE 6. Connecting the top and bottom edges of the rectangle on the left gives the cylinder on the upper right. Connecting left and right edges then gives a torus. Try to imagine overlaying the map in figure 5 onto the torus.
along the inner ring corresponded to the polar regions in the world map in figure 5? How could we have ruled this out in Columbus’s era? We could not have. Magellan could very well have circumnavigated the inner ring of a torus—or, indeed, the outer ring. And if the world were truly enormous, he may have just gone from outer to inner and back again, tracing what might be called a bite-size trajectory on the torus.
To return to the map in figure 3, suppose that it had turned out that our world was such that one could keep going north forever, and similarly to the south. In this case, our world would have been shaped like an infinitely long cylinder.
We conclude that we could not know the shape of our world with absolute certainty until it had been charted with complete precision—all regions including the poles. And the poles and interiors of some continents were not mapped until the nineteenth century.
Popular accounts of mathematics often stress the discipline’s obsession with certainty, with proof. And mathematicians often tell jokes poking fun at their own insistence on precision. However, the quest for precision is far more than an end in itself. Precision allows one to reason sensibly about objects outside of ordinary experience. It is a tool for exploring possibility: about what might be, as well as what is.
The discussion in the last chapter raised the possibility that the world could have been a torus. We don’t see doughnut shapes when we look up in the sky, so it takes some openness to possibilities to be willing to assume the Earth is one. Nowadays, we can get off the Earth and take a photograph from a satellite or spaceship. But in the era before space flight, it took an act of interpretative imagination to see the Moon and the Sun as spheres instead of flat disks facing us. The other planets and stars appear to be point sources. Rather than argue about what we are seeing in the heavens, let’s suppose that we cannot see beyond the Earth. Imagine that we live on a planet like Venus that is covered in cloud all the time. What shape might our planet be? Could it be something else other than a sphere or a torus?
Although these questions have been framed by asking you to imagine worlds whose shapes we know to be “wrong” in the ordinary sense, it is characteristic of mathematics that, time and again, such feats of imagination lead to new understandings and new structures that later prove to be exactly what is needed for a major scientific advance.
To go further, we need terminology that is clear and unambiguous. The most critical idea for us will be that of a two-dimensional manifold or surface. We arrive at this notion by thinking about possible shapes that a world might have, and it is relatively harmless to imagine two-dimensional manifolds as modeling worlds on which we might live. In particular, let us agree that a two-dimensional manifold or surface is a mathematical object all areas of which can be represented on some map on a sheet of a paper. The word two-dimensional refers to the fact that at any point on such an object, nearby points can be expressed in terms of two independent directions. This is important because mapmaking requires that we can determine how points are related to one another. We must be able to identify each. The maps, that is, the sheets on paper on which the points of the world are represented, are two-dimensional. A collection of maps that covers the surface, so that every point on the surface is represented on at least one of the maps, is called an atlas. If one purchases an atlas of the earth, one will get a book of maps, and one rightly expects that every location on earth appears in at least one of the maps. A two-dimensional manifold or surface, then, is an object represented by an atlas.
Several remarks are in order. First, two-dimensional manifolds are mathematical objects that are idealizations of physical reality. When we say that the earth is a sphere, we are saying that the mathematical object that is a sphere is a good model for the surface of the earth. Notice, by the way, that by a sphere, we mean the outside skin, or surface, of a ball. We do not include the stuff enclosed by the sphere. So that when we say the earth is a sphere, we are excluding the bedrock or magma beneath the surface. Likewise, a torus is any two-dimensional manifold that models the surface or skin of a doughnut. It does not include the inside. The extra precision we get by making careful definitions allows some strange objects, and we must be careful not to confuse physical considerations and mathematical ones. For us, a two-dimensional manifold is a set with the property that all points near a point can be represented on a map. That’s all. Mathematicians use the word surface as synonymous with two-dimensional manifold, although not every two-dimensional manifold is the surface of some solid.17 Nor is it always possible to consistently define right and left on a manifold.18 However, it turns out that any two-dimensional manifold on which it is possible to consistently define left and right can be represented as the surface of some solid, and vice versa. Such two-dimensional manifolds are called orientable.19
Another crucial thing to keep in mind is the use of the word dimension. In the casual usage of everyday speech, one will often hear assertions such as the Earth (or a sphere) or a torus is three-dimensional because one needs a three-dimensional space in which to fully fit it. We will never use dimension in this way. For us, dimension refers to the number of independent directions needed to represent all points on an object near a given point. If we tried to put all the maps in an atlas together to get a sort of globe that represented the surface more holistically, we will certainly need a third dimension (or more), but we still refer to the manifold or surface as being two-dimensional. The dimension refers to the number of independent directions that someone who lived on the manifold would experience, not the number of dimensions that we need to fit the object into.20