Inhaltsverzeichnis
Einleitung
Konventionen in diesem Buch
Törichte Annahmen über den Leser
Was Sie in diesem Buch finden
Was Sie in diesem Buch nicht finden
Wie dieses Buch aufgebaut ist
Teil I: Einführung
Teil II: Vektorrechnung
Teil III: Matrizen
Teil IV: Lineare Gleichungssysteme
Teil V: Der Top-Ten-Teil
Spickzettel
Symbole, die in diesem Buch verwendet werden
Wie es weitergeht
Teil I Einführung
Kapitel 1
Motivation
Gestatten: Die Familie der Vektoren, Matrizen und linearen Gleichungssysteme
Vektoren in Theorie und Praxis
Matrizen in Schule, Studium und Beruf
Wie Matrizen behandelt werden wollen und wie sie einem behilflich sind
Kapitel 2
Vektorrechnung
Was war zuerst da: der Vektor oder der Pfeil?
Voll konkret: explizite Schreibweise und Komponenten eines Vektors
Der Betrag eines Vektors
Beispiele
Einheitsvektoren – Voll normal!
Rechnen mit Vektoren
Addition und Subtraktion von Vektoren
Multiplikation von Vektoren mit Zahlen
Linearkombination von Vektoren als »Pfeile«
Differenzvektoren
Vektoren in der analytischen Geometrie
Die Winkelhalbierenden eines Dreiecks
Zum Halten von Lasten
Kapitel 3
Matrizen
Definition und Form von Matrizen
Rechnen mit Matrizen – mehr als nur ein Haufen Zahlen!
Addition und Subtraktion von Matrizen
Multiplikation von Matrizen
Invertieren von Matrizen
So sieht sich eine Matrix im Spiegel
Der Stammbaum der Matrizen
Reelle und komplexe Matrizen
Quadratische und nicht-quadratische Matrizen
Reguläre und singuläre Matrizen
Symmetrische und hermitesche Matrizen
Orthogonale und unitäre Matrizen
Dreiecksmatrizen
Noch speziellere Matrizen ...
Matrizen bei der Arbeit
Determinante und Umkehrbarkeit von Transformationen
Eigenwerte, Eigenvektoren und das Diagonalisieren von Matrizen
Kapitel 4
Lösen von linearen Gleichungssystemen
Matrixschreibweise für lineare Gleichungssysteme
Links- und Rechtsmultiplikation sind zweierlei!
Umformen der Koeffizientenmatrix eines linearen Gleichungssystems
Teil II Vektorrechnung
Kapitel 5
Vektor mal Vektor = ???
Skalarprodukt: Vektor mal Vektor gleich Zahl
Definition und Schreibweisen
Wissenswertes zum Skalarprodukt: kurz und knapp
Geometrische Bedeutung – endlich wird es anschaulich!
Wie berechnet man das Skalarprodukt konkret?
Kreuzprodukt: Vektor mal Vektor gleich Vektor
Definition und Schreibweise
Nützliches zum Vektorprodukt: wieder kurz und knapp
Geometrische Bedeutung – endlich wird's wieder anschaulich!
Wie rechnet man das Kreuzprodukt konkret aus?
Das Spatprodukt – und was ist bitte ein Parallelepiped?
Dyadisches Produkt: Vektor mal Vektor gleich Matrix
Definition und Schreibweise
Dyadisches Produkt zweidimensionaler orthogonaler Einheitsvektoren
Dyadisches Produkt von orthogonalen Einheitsvektoren in drei Dimensionen
Kapitel 6
Die Welt der Mathematik besteht aus Vektoren ...
Unser Koordinatensystem ist das Gerüst der Vektor-Welt
Kartesische Koordinatensysteme – hier steht alles senkrecht!
Beispiele für kartesische Koordinatensysteme
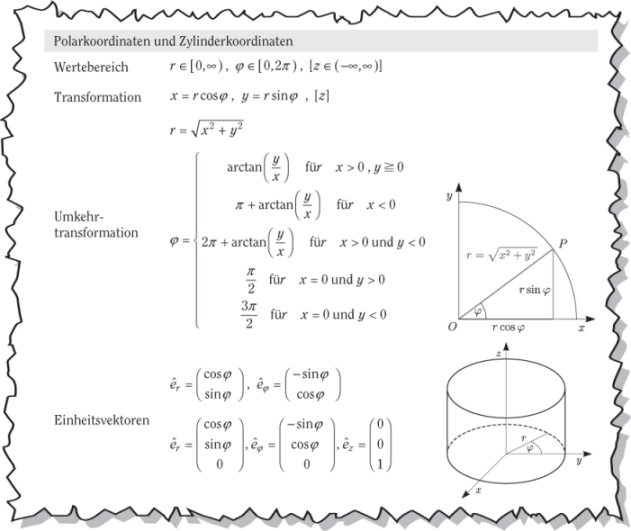
Polarkoordinaten – krumme Linien in der Ebene?!
Zylinderkoordinaten – Hut ab für die dritte Dimension!
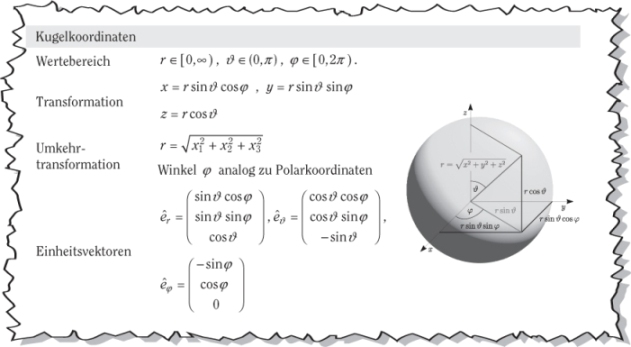
Kugelkoordinaten – eine runde Sache
Basis und Basistransformationen: Wir wechseln den Blickwinkel!
Unter der Lupe: Was versteht man unter einer Basis?
Beispiele für Basen
Basistransformationen – aus Alt mach Neu
Jetzt geht's rund – wir drehen die Basis!
Kapitel 7
Analytische Geometrie – mehr als nur ein paar Bauklötze!
Lineare Abhängigkeit und Unabhängigkeit von Vektoren
Der Vektorzug fährt ein ...
Parallele und antiparallele Vektoren
Anwendungsaufgabe zur linearen Abhängigkeit von Vektoren
Darstellung von Geraden und Ebenen
Parameterdarstellung: Jetzt kommen die Vektoren zum Zug!
Normalenform: Der senkrechte Vektor zeigt, wo es lang geht!
Zusammenfassung
Der Klassiker: Schnitte und Abstände von Geraden und Ebenen
Schnitte von Geraden mit Ebenen
Abstand zwischen Ebene und einer parallelen Gerade
Schnitt zweier Ebenen in Parameterdarstellung
Schnitt einer Ebene in Parameterdarstellung und einer Ebene in Normalenform
Bestimmung des Abstands zweier paralleler Ebenen
Parallele und windschiefe Geraden
Wir verlassen das Flachland und bauen Körper aus Ebenen
Eine Pralinenschachtel in der Vektorrechnung
Analytische Geometrie für Fortgeschrittene Teil 1: Wir bauen uns einen Tetraeder
Analytische Geometrie für Fortgeschrittene Teil 2: Wie viel Farbe benötigt man, um einen Dodekaeder anzumalen?
Die Sache kommt ins Rollen: Kugeln in der Vektorrechnung
Die Kugelgleichung
Tangentialebenen
Schnitt von Kugeln mit Ebenen
Kapitel 8
Funktionenräume
Können Funktionen Vektoren sein?
Ein Skalarprodukt für Funktionen
Lineare Abhängigkeit und Unabhängigkeit von Funktionen
Funktionen machen es den Vektoren im Anschauungsraum nach
Der Funktionenraum der Polynome
Monome als Bausteine von Polynomen
Orthogonale Funktionen – was bedeutet das?
Trigonometrische Funktionen
Auf der Suche nach einer Basis
Ran ans Werk: Das Skalarprodukt trigonometrischer Funktionen
Die Fourierreihe – wir bringen Funktionen zum Schwingen
So macht man aus unstetigen Funktionen stetige
Teil III Matrizen
Kapitel 9
Rechenregeln
Assoziativgesetz, Distributivgesetz und Kommutativgesetz für die Addition
Addition, Subtraktion und Multiplikation in Aktion
Division durch Bildung der Inversen
Lineare Abbildungen, Kern und Bild
Basistransformationen von Vektoren mittels Matrizen
Einführung in lineare Abbildungen und deren Basiswechsel
Kapitel 10
Determinanten
Verfahren nach Leibniz
Permutationen – da haben wir den (Zahlen)salat!
Die Determinantenformel
Schachbrettregel und Unterdeterminanten
Entwicklung nach Zeilen oder Spalten
Spezialfall: (2 x 2)-Matrizen
Spezialfall: (3 x 3)-Matrizen und Sarrussche Regel
Rechenregeln für Determinanten
Anwendung: Berechnung des Kreuzprodukts mit der Determinante
Kapitel 11
Invertieren von Matrizen
Regularität und Singularität als Indiz für Invertierbarkeit
Berechnung der Inversen mittels des Gauß-Algorithmus
Bildung der Inversen mittels der Adjunkten
Spezialfall: (2 × 2)- und (3 × 3)-Matrizen
Kapitel 12
Eigenwerte und Eigenvektoren, Diagonalisieren von Matrizen
Berechnung von Eigenwerten, algebraische Vielfachheit
Berechnung der Eigenvektoren, geometrische Vielfachheit
Diagonalisieren von Matrizen
Algebraische Vielfachheit = Geometrische Vielfachheit
Mehrfaches Auftreten von Eigenwerten
Algebraische Vielfachheit ≠ Geometrische Vielfachheit
Besonderheiten von symmetrischen und hermiteschen Matrizen
Was sich nicht ändert beim Diagonalisieren
Anwendung: Noch einmal Drehungen
Anwendung: Quadriken
Die Hauptachsen einer Quadrik
Anwendung des Verfahrens nach Gram und Schmidt
Ein paar Tipps zum Abschluss des Kapitels!
Für Fortgeschrittene: Jordansche Normalform
Bestimmung der Jordan-Normalform und der Transformationsmatrix
Kapitel 13
Besonders einfache Matrizen
Dreiecksmatrizen
Diagonalmatrizen
Blockdiagonale Matrizen
Teil IV Lösen von linearen Gleichungssystemen
Kapitel 14
Gauß-Algorithmus in Matrixschreibweise: Vertiefung
Erweiterte Koeffizientenmatrix und Zeilenstufenform
Rang von Matrizen
Systeme mit einer eindeutigen Lösung
Systeme ohne Lösung
Systeme mit unendlich vielen Lösungen
Kapitel 15
Lösen von linearen Gleichungssystemen mit Hilfe von Parametern
Einführung von Parametern und Bilden der Lösung
Minus-Eins-Ergänzungstrick: Erzeugung der Zeilennormalform und Ablesen der Lösung
Kapitel 16
Homogene und partikuläre Lösung
Bildung der homogenen Lösung
Bildung der partikulären Lösung
Zusammensetzen beider Lösungen
Kapitel 17
Lösungsweg unter Verwendung der Determinante
Aufstellen der zu berechnenden Determinanten und Cramersche Regel
Resultate aus der Cramerschen Regel
Anwendung: Lösbarkeit eines linearen Gleichungssystems in Abhängigkeit zweier Parameter
Anwendung: Die Wronski-Determinante
Die Wronski-Determinante in Aktion
Lineare Unabhängigkeit im Fall der Monome
Lineare Unabhängigkeit im Fall der Sinus- und Kosinusfunktionen
Teil V Der Top-Ten-Teil
Kapitel 18
Zehn häufige Anfängerfehler
Dividieren durch Vektoren – Nein!
Matrizen vertauschen nicht!
Ein Vektor hängt von den Komponenten und der Basis ab!
Verwirrung beim komplexen Skalarprodukt
Leichtsinnsfehler
Vektoren in anderen Koordinatensystemen
Einheitskreis – wie bitte?
Wurzelziehen aus Quadraten
Vorsicht mit der imaginären Einheit
Falsche Regeln bei der Berechnung von Determinanten
Kapitel 19
Zehn Tipps für erfolgreiche Prüfungen
Üben, üben, üben!
Nachdenken ist die halbe Miete!
Ergebnisse kritisch begutachten
Üben Sie auch möglichst an verschiedenen Aufgabentypen!
Gleichungen müssen stimmig sein!
Effizienz von Algorithmen
Aussehen von Geraden und Ebenen
Denken Sie sich selber Aufgaben aus!
Nehmen Sie nicht alles bierernst!
Denken Sie an die am häufigsten vorkommenden Fragen!
Stichwortverzeichnis
Vektor- und Matrizenrechnung für Dummies – Schummelseite
Bibliografische Information der Deutschen Nationalbibliothek
Die Deutsche Nationalbibliothek verzeichnet diese Publikation in der Deutschen Nationalbibliografie; detaillierte bibliografische Daten sind im Internet über http://dnb.d-nb.de abrufbar.
1. Auflage 2013
© 2013 WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim
All rights reserved including the right of reproduction in whole or in part in any form. This EBook published under license with the original publisher John Wiley and Sons, Inc.
Alle Rechte vorbehalten inklusive des Rechtes auf Reproduktion im Ganzen oder in Teilen und in jeglicher Form. Dieses E-Book wird mit Genehmigung des Original-Verlages John Wiley and Sons, Inc. publiziert.
Wiley, the Wiley logo, Für Dummies, the Dummies Man logo, and related trademarks and trade dress are trademarks or registered trademarks of John Wiley & Sons, Inc. and/or its affiliates, in the United States and other countries. Used by permission.
Wiley, die Bezeichnung »Für Dummies«, das Dummies-Mann-Logo und darauf bezogene Gestaltungen sind Marken oder eingetragene Marken von John Wiley & Sons, Inc., USA, Deutschland und in anderen Ländern.
Das vorliegende Werk wurde sorgfältig erarbeitet. Dennoch übernehmen Autoren und Verlag für die Richtigkeit von Angaben, Hinweisen und Ratschlägen sowie eventuelle Druckfehler keine Haftung.
Coverfoto: Fotolia/Lemonade
Satz: Beltz Bad Langensalza GmbH, Bad Langensalza
Print ISBN: 978-3-527-70742-3
ePub ISBN 978-3-527-66824-3
mobi ISBN 978-3-527-66825-0
Einleitung
Kennen Sie das? Sie sitzen zu Hause mit einem unangenehmen Gefühl in der Magengegend, weil in drei Wochen eine wichtige Matheprüfung ansteht. Das Gefühl kommt nicht von ungefähr, denn schließlich ist Ihnen klar, dass Sie alles andere als sattelfest im Prüfungsstoff sind. Deshalb haben Sie sich schnell aus der Bibliothek etliche Wälzer ausgeliehen, die jetzt auf Ihrem Schreibtisch liegen. Sicherlich liegt auch eine Mitschrift aus der Vorlesung, die Sie besucht haben, vor Ihnen. Leider ist Ihnen jedoch klar, dass Sie aus der Vorlesung nicht viel mitgenommen haben und der Tag der Prüfung sitzt Ihnen wie ein Nadelkissen im Nacken.
Ihre Mitschrift ist alles andere als ausführlich, deshalb beginnen Sie, eines der Bücher aufzuschlagen, bleiben jedoch bereits an einer der ersten Seiten hängen. Was also tun – aufgeben? Natürlich müssen Sie das nicht tun, denn Sie haben sich ja glücklicherweise für ein Buch aus der »¼ für Dummies«-Reihe entschieden. Gratulation! Sie halten ein Werk in den Händen, das Ihnen die wichtigsten Bereiche aus den Gebieten der linearen Algebra und analytischen Geometrie näher bringt.
Grundlage der linearen Algebra sind mathematische Objekte – Vektoren und Matrizen – mit denen man wie mit gewöhnlichen Zahlen rechnen kann. Selbstverständlich gibt es einige wesentliche Unterschiede. Mit Vektoren und Matrizen lässt sich viel mehr anstellen als mit einfachen Zahlen. Trifft Roger Federer mit seinem Schläger einen Tennisball, so fliegt dieser mit einer bestimmten Geschwindigkeit und Richtung durch die Luft. Die Geschwindigkeit können Sie mit einer Zahl angeben. An guten Tagen beträgt sie vielleicht 200 Kilometer pro Stunde. Doch wie sieht es mit der Richtung aus, wie kann man diese mit nur einer Zahl kennzeichnen? Kurzum, das geht nicht ohne Vektoren!
Die analytische Geometrie ist mehr als ein einfaches Teilgebiet der Geometrie. Während man in der Geometrie Probleme zeichnerisch angeht, werden in der analytischen Geometrie zusätzlich rechnerische Methoden zu Hilfe genommen.
Mit diesem Rüstzeug können Sie Problemstellungen unterschiedlichster Art angehen. Dazu gehört die Beschreibung von Geraden im Raum, von Flächen und Körpern. Ohne noch weiter auszuschweifen, packen wir es also an!
In diesem Buch werden Sie über eine große Menge an neuen Fachbegriffen stolpern. Immer wenn ein solcher Begriff auftaucht, der im Bereich des behandelten Themas eine Rolle spielt, wird dieser fett gedruckt. Ein Wort, das kein Fachbegriff ist, wird dann kursiv gedruckt, wenn damit etwas betont werden soll.
Mathematische Funktionen wie die Sinus-, Kosinus- und die Exponentialfunktion werden mit den typischen aufrecht gedruckten Bezeichnungen »sin«, »cos« und »exp« versehen. Ein Differential in Ableitungen oder in einem Integral wird mit einem aufrechten »d« bezeichnet; ebenso soll für die imaginäre Einheit ein aufrechtes »i« gebraucht werden: i2 = –1.
Die Schreibweise für sonstige mathematische Objekte und Formeln wird an gegebener Stelle erklärt.
Da Sie sich für dieses Buch entschieden haben, erlauben wir uns eine Einschätzung Ihrer Person. Wie oben beschrieben kann es sein, dass Sie einem technischen oder naturwissenschaftlichen Studiengang angehören und demnächst eine Prüfung ansteht. Natürlich ist es auch möglich, dass Sie Grundkenntnisse der linearen Algebra aus beruflichen Gründen benötigen. Vielleicht sind Sie aber einfach »nur« ein bisschen an höherer Mathematik interessiert, Mathematik ist also Ihr Hobby?
Was auch immer genau der Fall ist – eines gilt mit Sicherheit: Sie haben keine Zeit oder Lust, sich durch dicke Wälzer zu quälen, die sich nur mit der grauen Theorie, aber ansonsten nicht mit Anwendungen befassen.
Wir vermuten, Sie kennen sich gut mit den Grundrechenarten aus und bringen einige (wenige) Grundlagen aus der Analysis mit. Sie wissen also vielleicht ein bisschen etwas über grundlegende Funktionen und können einfache Ableitungen und Integrale ausrechnen. Sollte letzteres nicht der Fall sein, lassen Sie sich jedoch bitte nicht abschrecken! Derartiges Wissen ist nur an einzelnen Stellen nötig und wird gegebenenfalls erklärt.
Das vorliegende Buch bietet eine anschauliche und leicht verdauliche Hinführung zu den wichtigsten Themen der linearen Algebra und der analytischen Geometrie. Die Thematik wird anhand konkreter Anwendungen eingeführt und behandelt. Eine grundlegende Philosophie stellt die Präsentation aussagekräftiger Beispiele dar. Eine Politik der Trivialbeispiele, wie sie oft in mathematischer Literatur betrieben wird, verfolgen wir nicht. Darüber hinaus können Sie sich auf hilfreiche Tipps und Tricks zur Lösung bestimmter Problemstellungen und Aufgaben freuen.
Das Buch ist nicht dafür gedacht, eine exakte und penible Behandlung der mathematischen Themen anhand des sonst üblichen Schemas »Definition« – »Satz« – »Beweis« zu liefern. Ebenso haben wir uns dazu entschlossen, zugunsten der Verständlichkeit und Anschaulichkeit auf manche für die Praxis unwichtige Sonderfälle keine Rücksicht zu nehmen. Sie machen einem das Leben zwar schwerer, aber der Nutzgewinn bleibt aus, wenn man sich eher für Anwendungen interessiert als für die Theorie.
Das Buch besteht aus fünf Teilen sowie dem Spickzettel. Jedem Thema ist ein einzelner Teil gewidmet bzw. in der Einführung ein einzelnes Kapitel.
Der einführende Teil nimmt zu allen folgenden Themen im Buch Stellung. Dazu gehören die Vektorrechnung, Matrizen und lineare Gleichungssysteme. Jedes dieser Themen wird anschaulich motiviert, und die grundlegendsten Begriffe werden erklärt. Weiterhin sollen hier bereits einfache Beispiele geliefert werden, da anhand konkreter Anwendungen der Einstieg sehr viel leichter fällt.
Sowohl Vektoren als auch Matrizen werden bereits hier eingeführt und die einfachen Rechenoperationen erklärt.
Nach der Einführung steigen Sie direkt in eine Weiterführung der Vektorrechnung ein. Da Sie dann bereits wissen werden, was ein Vektor überhaupt ist, geht es damit weiter, was sich mit Vektoren in der Anwendung alles machen lässt. Sie werden sehen, wie man geometrische Figuren wie beispielsweise Geraden und Ebenen in der Vektorrechnung darstellt und wie Sie elementargeometrische Probleme mit Methoden aus der Vektorrechnung lösen können.
Weiter geht es mit den Matrizen. Hier lernen Sie, dass Vektoren nichts anderes sind als spezielle Matrizen. Also ist der Matrixbegriff im Prinzip eine Erweiterung des Vektorbegriffs. Es gibt viele verschiedene Arten von Matrizen. Jeder dieser Typen lässt sich für unterschiedliche Aufgaben verwenden und unterscheidet sich in den Eigenschaften von den anderen Typen. Es geht also zunächst darum, dass Sie eine Matrix sofort in eine dieser Gruppen einordnen können und ihre Eigenschaften erkennen, sofern Sie sie sehen. Danach werden wir Ihnen zeigen, wozu Sie Matrizen in der Anwendung verwenden können.
Eine wichtige Anwendung von Matrizen stellt die Lösung linearer Gleichungssysteme dar. Deshalb ist diesen ein kompletter, wenn auch kurzer Teil, gewidmet. Hier werden Sie lernen, wie Sie ein solches Gleichungssystem mittels Matrizen darstellen können und wie Sie die Anzahl der Lösungen bzw. die genaue Gestalt der Lösung ermitteln.
Mit der Behandlung linearer Gleichungssysteme sind alle Themen des Buchs abgehandelt. Was hier kommt, ist eine Zusammenstellung nützlicher Tipps im Rahmen des behandelten Materials.
Auf dem Spickzettel sind die wichtigsten Formeln und Zusammenhänge für Vektoren und Matrizen zusammengefasst. Erinnern Sie sich nicht mehr an eine bestimmte Definition, an eine Formel oder an Rechenregeln, dann ist der Spickzettel Ihr Freund.
Das Erinnerungssymbol wird immer dann verwendet, wenn eine Aussage gemacht oder eine Formel eingeführt wird, die Sie sich merken sollten. Hier stehen ausschließlich wichtige Dinge, die Sie im Bereich Vektor- und Matrizenrechnung immer wieder benötigen könnten.
Dabei handelt es sich um einen Tipp, welcher an dieser Stelle hilfreich ist. Es ist sinnvoll, sich diese Tipps zu merken und bei Bedarf wieder in Erinnerung zu rufen.
Vorsicht ist geboten, wenn Sie dieses Symbol sehen! Damit möchten wir Sie auf mögliche Stolperfallen und etwaige Fehlerquellen aufmerksam machen.
Es ist alles gesagt. Sie können nun sofort anfangen, in dem Buch zu blättern und zu lesen! Besitzen Sie einiges an Vorkenntnissen oder möchten Ihre Erinnerung auffrischen, können Sie im Prinzip auf das einleitende Kapitel verzichten. Ist das nicht der Fall, legen wir Ihnen nahe, die Einführung durchzulesen. Hier nehmen wir einige Dinge bereits vorweg, die in den späteren Kapiteln manchmal zwar noch kurz wiederholt, aber ansonsten direkt verwendet werden.
Es ist immer sinnvoll, ein Buch über mathematische Themen nicht einfach »nur« zu lesen, sondern die einzelnen Beispiele und Berechnungen parallel dazu selbst durchzuarbeiten. Wenn Ihnen das möglich ist, dann haben Sie die Gewissheit, dass Sie es auch wirklich verstanden haben, und das ist ein tolles Gefühl.
Teil I
Einführung
In diesem Teil ...
Die Geometrie hat ihren Ursprung in der Zeit der frühen Hochkulturen. Bei den alten Ägyptern entwickelte sie sich als Werkzeug zur Landvermessung, die nach jeder Nilüberschwemmung von neuem durchgeführt werden musste. Das Wort Geometrie kommt aus dem Griechischen und bedeutet so viel wie »Vermessung der Erde«. Im Altertum befasste sie sich vor allem mit der Durchführung zeichnerischer Konstruktionen mit Zirkel und Lineal, Winkeln und Ähnlichkeitsbeziehungen von Dreiecken. Mit diesen Themen beschäftigt man sich heutzutage vor allem in der Schule.
Andererseits lassen sich geometrische Probleme auch rechnerisch angehen, ohne auf die Anschauung zurückzugreifen. Dieses Vorgehen läuft unter der Bezeichnung analytische Geometrie. Letztere ist im Prinzip ein Unterbegriff der linearen Algebra, die sich mit Vektoren und linearen Abbildungen zwischen Vektoren beschäftigt.
In der Einführung lernen Sie die grundlegenden Begriffe und Vorgehensweisen in der Vektorrechnung kennen, also was Vektoren überhaupt sind und wozu man sie gebrauchen kann. Anfangs wird eine Einteilung der entsprechenden Gebiete vorgestellt, die Themen dieses Buchs sind. Dazu gehören das Rechnen mit Vektoren an sich sowie weiterführende Kniffe, die Ihnen die Anwendung von Vektoren auch dann erlauben, wenn das zuvor nicht unbedingt ersichtlich war.
Danach möchten wir Ihnen mit kleinen anschaulichen Häppchen diese Gebiete schmackhaft machen. Dabei können Sie sich bereits auf das Hauptmenü ab dem zweiten Teil des Buchs freuen, wo Sie Ihr Wissen anhand vieler Anwendungen vertiefen werden.
1
Motivation
In diesem Kapitel ...
Motivation und Vorstellung der Themenbereiche in der Vektorrechnung
Verzahnung und Zusammenwirken der einzelnen Bereiche
Eine Matheklausur ist wie eine Schachtel Pralinen – man weiß nie, was drankommt. Deshalb möchte dieses Buch einen umfangreichen Überblick über die stark miteinander verknüpften Themengebiete der Vektorrechnung, Matrizen und linearen Gleichungssysteme liefern. Das Ziel ist, dass sich der Leser ein tiefgründiges Verständnis aneignen kann und dadurch nicht nur für die nächste Klausur bestens gewappnet ist, sondern auch über eine solide Basis in Sachen linearer Algebra und analytischer Geometrie verfügt.
Dabei verzichten wir auf eine trockene Darstellungsweise in Form von Definitionen, Sätzen und anschließenden Beweisen, sondern möchten der Mathematik Leben einhauchen, indem wir den Schwerpunkt auf die anwendungsorientierte Seite legen. Das bedeutet nicht, dass wir komplizierte Fragestellungen geschickt umschiffen. Stattdessen werden alle Themen in einer handfesten und anschaulichen Form präsentiert, die das Erlernen erleichtert.
Die Vektorrechnung beschäftigt sich, wie der Name bereits verrät, mit Vektoren genannten mathematischen Objekten, die sich von gewöhnlichen Zahlen drastisch unterscheiden, sowohl was ihre Eigenschaften angeht als auch was den Umgang mit ihnen betrifft.
Der nächste große Teil des Buchs beschäftigt sich mit Matrizen. Im Prinzip handelt es sich bei einer Matrix um eine Weiterführung des Vektorbegriffs. Eine Matrix ist nichts anderes als ein rechteckiges Zahlenschema. Wenn Sie schon einmal Sudoku gespielt haben, haben Sie sich zumindest unbewusst bereits mit Matrizen beschäftigt. Mit Matrizen kann man rechnen, und sie lassen sich vielfältig auch in der Vektorrechnung einsetzen.
Danach sollen Gleichungssysteme behandelt werden. Dabei handelt es sich um eine Menge von Gleichungen mit mindestens zwei Unbekannten. Wir wollen Ihnen ausschließlich den Umgang mit linearen Gleichungen demonstrieren, in denen Unbekannte einzig und allein in der ersten Potenz vorkommen. Wie man ein solches System lösen kann, ist bereits Schulstoff. Doch das Ziel ist es, mittels Vektorrechnung und Matrizen diese Methoden zu verallgemeinern und zu verfeinern.
Die Vernetzung zwischen den Bereichen untereinander, wie sie in diesem Buch eine Rolle spielt, ist in Abbildung 1.1 veranschaulicht. Die eingezeichneten Pfeile stellen mögliche Verbindungen dar. Wir haben uns dazu entschieden, die Gebiete in der zuvor genannten Reihenfolge zu behandeln, da man die Vektorrechnung erlernen kann, ohne etwas über die anderen Themen zu wissen. Zwar können sowohl Matrizen als auch lineare Gleichungssysteme in der Vektorrechnung ihre Anwendung finden, sie sind jedoch nicht zwingend notwendig.
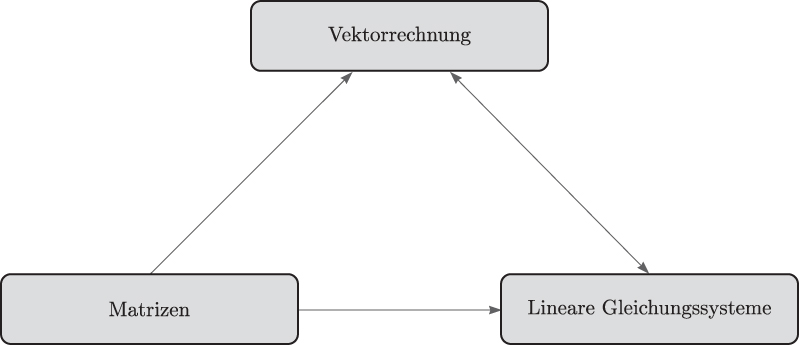
Abbildung 1.1: Die behandelten Gebiete und wie sie zusammenhängen
Die Vektor- und Matrixrechnung halten Einzug in lineare Gleichungssysteme. Wie gesagt, kann man letztere auch ohne solche Kenntnisse lösen, jedoch lassen sie sich mit derartigen Methoden systematisch angehen, was besonders für Gleichungssysteme mit mehr als drei Unbekannten vorteilhaft ist.
Lineare Gleichungssysteme und Matrizen selbst können ihrerseits in Problemstellungen der anderen Disziplinen einfließen.
In der gymnasialen Oberstufe kommt man zum ersten Mal mit der analytischen Geometrie in Berührung. Hier führt man den Vektorbegriff sehr anschaulich ein als ein mathematisches Objekt, das man als Pfeil im Koordinatensystem darstellen kann. Ein solcher Pfeil zeigt in eine bestimmte Richtung und besitzt darüber hinaus eine Länge. Somit können Vektoren als Größen verstanden werden, die sowohl eine Richtung angeben als auch eine Länge haben. Vektoren sind also etwas komplett anderes als gewöhnliche Zahlen. Doch mit dem Vektorbegriff allein kann man noch nicht allzu viel anfangen. Man muss ja mit Vektoren auch rechnen können. Beispielsweise entspricht die Addition von Vektoren dem Aneinanderlegen von Pfeilen im Koordinatensystem.
Dieses Vorgehen, das von der Schule her bekannt ist, sucht in einer Mathematikvorlesung an der Universität seinesgleichen. Denn hier wird der Vektorbegriff viel allgemeiner behandelt, was jedoch auf Kosten der Anschaulichkeit geht. Es geht dann nicht mehr darum, dass man Pfeile in Koordinatensysteme zeichnet, sondern dass Vektoren als abstrakte Größen behandelt werden, für die bestimmte Grundregeln, sogenannte Axiome, gelten. Es ist jedoch so, dass in der Praxis oft die anschauliche Vorstellung von Vektoren ausreichend ist, wie man sie in der Schule kennengelernt hat.
In den Ingenieurwissenschaften lassen sich beispielsweise mit Hilfe von Vektoren Kräfte beschreiben, die innerhalb einer gegebenen Anordnung wirken, wie zum Beispiel einem Flaschenzug. Kräfte besitzen einen Angriffspunkt, zeigen in eine bestimmte Richtung und haben außerdem eine bestimmte Größe. Nicht umsonst stellt man sie in Skizzen als Pfeile dar. Das Ganze schreit förmlich nach dem Vektorbegriff.
Soll die Bahn eines elektrisch geladenen Teilchens in der Nähe eines Magneten beschrieben werden, so kann auch dies mit Vektoren erfolgen. Die Flugbahn ergibt sich aus der Kraft, die der Magnet auf das Teilchen ausübt. Man kann sowohl die Flugbahn als auch die Kraft mittels Vektoren beschreiben. Zum einen bewegt sich das Teilchen auf seiner Bahn in eine bestimmte Richtung, und legt eine Wegstrecke zurück. Zum anderen zeigen die Kraftlinien in eine Richtung, und die Kraft selbst besitzt zudem eine gewisse Stärke. Das sind Problemstellungen, die wie geschaffen sind für eine Anwendung der Vektorrechnung.
Stellvertretend für ein rechtwinkliges Zahlenschema hat der Begriff der »Matrix« schon lange Einzug in die Mathematik gehalten. Leuten, die Sudoku spielen oder sich mit magischen Quadraten beschäftigen, sind solche Schemata durchaus bekannt. In der Mathematik umfasst man die Zahlen darüber hinaus mit einem Paar runder Klammern, wie beispielsweise:
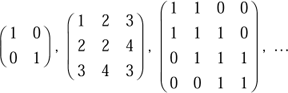
Doch was bringen solche Anordnungen von Zahlen außer Spielerei? Das kann doch nicht alles sein! Das ist es auch nicht, denn mit Matrizen kann man unglaublich viel machen. Wie Zahlen und Vektoren lassen sich auch Matrizen addieren und multiplizieren, wobei die Rechenregeln nur unter bestimmten Voraussetzungen funktionieren. Wo auch immer sich Vektoren tummeln, sind Matrizen nicht weit. Im Prinzip sind Vektoren nichts anderes als eine spezielle Klasse von Matrizen. Beispielsweise kann eine Matrix unter bestimmten Voraussetzungen mit einem Vektor multipliziert werden, woraus dann ein neuer Vektor hervorgeht. Mit Hilfe von Matrizen können also Vektoren auf eine bestimmte Art und Weise geändert werden. Also kann eine Matrix so etwas wie ein Operator sein, der einen Vektor manipuliert, ihn beispielsweise dreht.
In einer Mathematikvorlesung werden Matrizen – ähnlich wie Vektoren – gewöhnlich als mathematische Objekte auf abstraktem Niveau eingeführt, für die bestimmte Grundregeln gelten. Auf eine solche Darstellung wird in diesem Buch verzichtet; stattdessen stehen praktische Anwendungen im Vordergrund.
Man begegnet Matrizen im Studium jedoch nicht nur in der Mathematikvorlesung, sondern auch in den angewandten Wissenschaften. Wichtig sind sie in der klassischen Mechanik, in der die Antwort ausgedehnter Körper oder elastischer Massen wie Gummi auf Kräfte durch charakteristische Matrizen beschrieben wird. Einfache Zahlen reichen dafür nicht aus, denn das Verhalten eines ausgedehnten Körpers auf eine Kraft hängt auch davon ab, wo die Kraft am Körper wirkt.
Darüber hinaus sind Matrizen überaus wichtig in der Atomphysik und spielen daher auch eine Rolle zur Beschreibung chemischer und biologischer Prozesse. Nach den quantenmechanischen Grundregeln befindet sich ein Atom oder ein Molekül in einem »Zustand«, der mathematisch als Vektor aufgefasst werden kann. Ein äußerer Einfluss wie die Einstrahlung von Licht ändert den Zustand des Atoms, was man mathematisch dadurch beschreibt, dass eine solche Änderung durch Multiplikation des Zustandsvektors mit einer Matrix erfolgt.
Wichtig sind Matrizen ebenso in den Wirtschaftswissenschaften, der Numerik sowie in allen anderen Bereichen, in denen Zahlen eine Rolle spielen. Daher wird man mit Matrizen höchstwahrscheinlich auch noch nach dem Studium in Berührung bleiben.
Was haben geometrische Figuren mit Gleichungssystemen zu tun? Eigentlich alles, denn hinter jeder Gleichung steht im Prinzip eine Menge von Punkten, die in ihrer Gemeinsamkeit eine geometrische Form bilden. In der Ebene oder im dreidimensionalen Raum kann man eine solche Menge anschaulich darstellen. In höherdimensionalen Räumen geht die Anschauung leider verloren, was aber nichts an der erwähnten Tatsache ändert. Es gibt zwei Klassen von Gleichungen: lineare und nichtlineare.
Der Einfachheit halber soll sich die Betrachtung zunächst auf die Ebene beschränken. In diesem Zusammenhang spielen Gleichungen eine Rolle, die maximal zwei Unbekannte enthalten. Diese werden als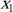 
und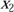 
bezeichnet. Kommen in einer Gleichung Terme vor, in denen die Variablen miteinander oder untereinander multipliziert werden, dann handelt es sich um eine nichtlineare Gleichung. Beispielsweise sind die folgenden Gleichungen nichtlinear:
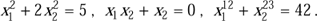
Derartige Gleichungen stellen Formen in der Ebene dar, die durch krumme Linien gekennzeichnet sind: Kreise, Ellipsen, Parabeln usw.
Dagegen sind Gleichungen, bei denen die Variablen höchstens zur ersten Potenz und auch nicht miteinander multipliziert auftreten, linear:
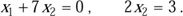
Geometrisch sind solche linearen Gleichungen (in zwei Dimensionen) nichts anderes als Geraden. Das lässt sich bereits anhand des lateinischen Ausdrucks »linea« vermuten, was »Linie« bedeutet. Teile von Geraden kann man mit dem Lineal zeichnen – soweit also zur Begriffsbildung.
Das Interesse besteht oft nicht nur für einzelne Gleichungen, sondern für Mengen mehrerer Gleichungen, die man Gleichungssysteme nennt. Steckt hinter einer einzigen Gleichung eine geometrische Figur, so handelt es sich bei einem System von Gleichungen dementsprechend um mehrere Figuren. Die erste Skizze aus Abbildung 1.2 besteht aus zwei Kreisen und gehört zu folgendem nichtlinearen Gleichungssystem:
(1) 
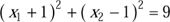
(2) 
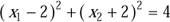
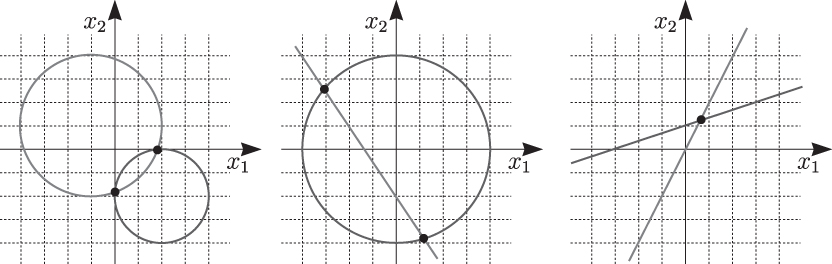
Abbildung 1.2: Geometrische Formen in der Ebene stehen für Gleichungen mit zwei Variablen
Die zweite Skizze mit dem Kreis und der Geraden ist eine graphische Darstellung des nächsten nichtlinearen Systems:
(1) 
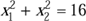
(2) 
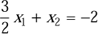
Zu guter Letzt veranschaulicht die dritte Skizze das nachfolgende lineare Gleichungssystem:
(1) 
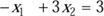
(2) 
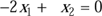
Nun besteht die Aufgabe darin, Gleichungssysteme zu lösen. Die Lösung setzt sich aus Punkten zusammen, die sowohl auf der einen als auch auf der anderen geometrischen Figur liegen. Es handelt sich dabei somit um Schnittpunkte der Figuren. Nichtlineare Gleichungen zu lösen kann mitunter überaus kompliziert und zum Teil nur numerisch möglich sein; daher wird in diesem Buch nur die Lösung linearer Gleichungssysteme behandelt.
Eine Anwendung von Matrizen liegt bei linearen Gleichungssystemen. Die Zahlen vor den Unbekannten – die Koeffizienten – lassen sich in eine Matrix packen. Für das letztere Gleichungssystem würde die entsprechende Matrix wie folgt lauten:
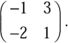
Das Gleichungssystem lässt sich auf diese Weise systematischer schreiben. Wie das genau funktioniert, lernen Sie im Kapitel »Lösen von linearen Gleichungssystemen«. Die Untersuchungen der Eigenschaften von solchen Matrizen führen zu allgemeinen Aussagen über die Lösbarkeit des Gleichungssystems sowie über die Anzahl der Lösungen.
2
Vektorrechnung
In diesem Kapitel ...
Der Vektorbegriff und die Schreibweise von Vektoren
Betrag eines Vektors und Einheitsvektoren
Einfaches Rechnen mit Vektoren und Anwendungen
Mathematiker behandeln Vektoren als Objekte, für die sie bestimmte Eigenschaften fordern. Diese Herangehensweise kann für Leute, die eher praxisorientiert sind, schwer verdaulich und zunächst auch langweilig sein. Es ist jedoch auch so, dass man in der Praxis mit dem Begriff des Vektors sehr lax umgeht. Ein Vektor wird dann als etwas betrachtet, das sowohl eine Größe hat als auch eine Richtung angibt. Hier möchten wir Ihnen die Eigenschaften von Vektoren zeigen und erklären, wie Sie mit Ihnen umgehen können. Das erfolgt zum Teil überaus anschaulich, also wird auf eine abstrakte mathematische Denkweise zunächst verzichtet.
Vektoren begegnen einem überall dort, wo man mathematisch etwas beschreiben muss, das außer einem Wert noch eine bestimmte Richtung hat. Dabei ist es unerheblich, ob man eine gegebene Problemstellung in der Ebene oder im dreidimensionalen Raum betrachtet. Man kann mit Vektoren sogar in abstrakten höherdimensionalen Räumen arbeiten. Doch wir begnügen uns größtenteils mit zwei und drei Dimensionen, da Aufgaben meistens derart gestrickt sind. Dann lassen sich Vektoren anschaulich als Pfeile mit einer bestimmten Länge darstellen.
Bevor wir uns in langen Erklärungen verzetteln, sollten Sie zunächst wiederholen, was ein Koordinatensystem ist, bevor Sie sich dem Vektorbegriff widmen können.
Ein Koordinatensystem ist ein Gebilde mit Achsen, das es einem erlaubt, die Position eines Punktes – die Koordinaten – durch dessen Lage bezüglich der Achsen anzugeben. Deshalb heißen die Achsen auch Koordinatenachsen. Jede Achse sollte die Bezeichnung der Variablen tragen, die entlang der Achse abgetragen wird: zum Beispiel x. Üblicherweise spricht man dann von der x-Achse. Jeweils zwei Koordinatenachsen liegen in Ebenen, die man Koordinatenebenen nennt. Beispielsweise liegen die x- und die y-Achse in der x–y-Ebene.
Veranschaulicht ist das Ganze in Abbildung 2.1. Koordinatensysteme werden im Abschnitt »Unser Koordinatensystem ist das Gerüst der Vektorwelt« im zweiten Kapitel von Teil II in aller Ausführlichkeit behandelt.
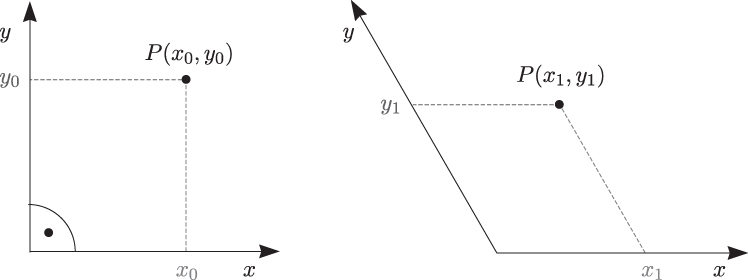
Abbildung 2.1: Zwei verschiedene Koordinatensysteme und die Darstellung eines Punktes P
Wie Sie sehen, gibt es unterschiedliche Koordinatensysteme. Das bekannteste kennen Sie bereits aus der Schule: das kartesische, bei dem die Achsen rechtwinklig aufeinander stehen. In beiden Systemen der genannten Abbildung ist jeweils ein Punkt P eingezeichnet, dessen Lage bezüglich der Achsen im linken Koordinatensystem mit den Koordinaten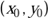 
und im rechten mit 
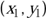eindeutig beschrieben wird. Sofern die Koordinaten zweier Punkte gleich sind, handelt es sich auch um denselben Punkt. Die Schreibweise ist gewöhnlich so, dass man die einzelnen Koordinaten waagerecht nebeneinander schreibt, jeweils durch ein Komma voneinander trennt und sie mit einem runden Klammerpaar umschließt.
Außerdem besitzt jedes Koordinatensystem einen sogenannten Ursprung (auch manchmal Koordinatenursprung genannt), der zukünftig immer als »O« bezeichnet wird. Dabei handelt es sich um den Schnittpunkt der Koordinatenachsen. Die Nomenklatur »O« steht ursprünglich für das lateinische Wort »origo«, das nichts anderes als Ursprung bedeutet. Heutzutage betrachtet man das »O« aber auch gerne als eine Null, da man im Ursprung auf allen Achsen den Wert null einträgt.
Einen Vektor kann man sich dann als Pfeil vorstellen, der zwei Punkte miteinander verbindet. Schauen Sie sich das Ganze bitte konkret in Abbildung 2.2 an.
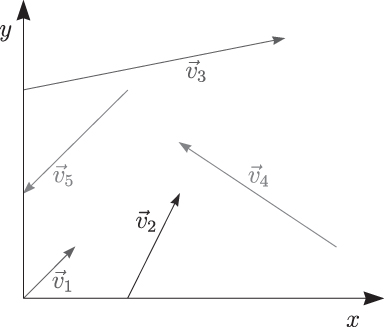
Abbildung 2.2: Allerhand verschiedene Vektoren in der Ebene
Hier sind in einem zweidimensionalen rechtwinkligen Koordinatensystem fünf Pfeile eingezeichnet, die stellvertretend für Vektoren stehen. Jeder einzelne dieser Pfeile besitzt eine Länge und zeigt in eine Richtung. Es ist dabei übrigens vollkommen unwichtig, wo man den Anfangspunkt des Pfeils hinlegt. Ein Vektorpfeil lässt sich beliebig innerhalb eines Koordinatensystems umherschieben; es bleibt trotzdem immer derselbe Pfeil, der stellvertretend für einen Vektor steht.
Vektoren bezeichnet man symbolisch meistens mit lateinischen oder griechischen Buchstaben. In der Anwendung werden Vektoren oft zusätzlich mit einem Pfeil versehen, also schreibt man zum Beispiel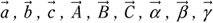 
usw. Manchmal werden Vektoren auch fett gedruckt oder unterstrichen: a, b, c oder a, b, c. Für dieses Buch fällt die Wahl auf die Möglichkeit, Vektoren mit Pfeilen zu kennzeichnen.
Vektoren lassen sich jedoch nicht nur symbolisch darstellen; es gibt auch eine explizite Schreibweise. Darum geht es im nächsten Abschnitt.
Abbildung 2.3 zeigt zwei verschiedene Koordinatensysteme, von denen das linke das rechtwinklige aus Abbildung 2.2 ist.
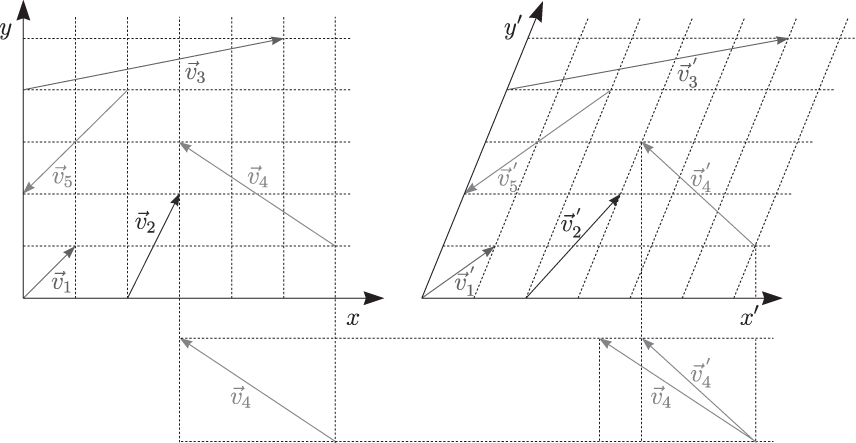
Abbildung 2.3: Fünf Vektoren in unterschiedlichen Koordinatensystemen
Beide enthalten je fünf Vektoren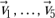 
bzw.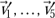 
. Zusätzlich wurde ein Netz aus gestrichelten Linien parallel zu den Koordinatenachsen eingezeichnet. Man bezeichnet jene als Gitternetzlinien oder Koordinatenlinien. Der jeweils vierte Vektor ist für beide Systeme zusätzlich noch einmal dargestellt, um sie direkt miteinander vergleichen zu können.
Es wird schnell klar, dass man zweierlei Informationen benötigt, um einen Pfeil zu zeichnen. Erstens ist es wichtig, wie viele Kästchen in Richtung der Koordinatenachsen abgetragen werden müssen. Zweitens muss man notwendigerweise wissen, wie die Gitternetzlinien aussehen, sprich das Koordinatensystem. Nur unter dieser Voraussetzung ist es möglich, die gegebene Anzahl von Kästchen entlang der Achsen abzutragen, um die Richtung eines Pfeils festzulegen.
Die Strecken entlang der Achsen eines Koordinatensystems nennt man Komponenten des Vektors. Liegt ein Vektor in der Ebene, so besitzt er zwei Komponenten. Man kann einen Pfeil in der Ebene ja nur dann zeichnen, wenn man weiß, wie viele Einheiten entlang der ersten und der zweiten Achse abgetragen werden müssen. Entsprechend sind für einen dreidimensionalen Vektor drei Komponenten notwendig usw.
Zu jedem Punkt in einem Koordinatensystem kann man sich einen Vektor denken, der am Schnittpunkt der Koordinatenachsen beginnt und am jeweiligen Punkt endet. Jeder Punkt lässt sich also auch als Vektor darstellen. Ein Vektor, der stellvertretend für einen Punkt steht, heißt Ortsvektor.
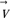in der Ebene bedeutet das: