

Teil 1
Analogtechnik
Die Elektronik ist ein breit gefächertes und in den letzten Jahrzehnten stark angewachsenes Fachgebiet, in dem man als Neuling leicht den Überblick verlieren kann. Besonders schwierig ist es daher, einen geeigneten Einstieg zu finden. Obwohl heute die digitale Elektronik zum Beispiel in der Computertechnik weiter verbreitet ist, finden sich in der analogen Elektronik, die bereits seit den Anfängen der Radiotechnik entwickelt wurde, die entscheidenden Grundlagen, an denen man nicht vorbeigehen sollte. Es werden zunächst keine Grundkenntnisse vorausgesetzt. Vielmehr soll der Analogteil des Buches ein solides Fachwissen von Grund auf vermitteln.
Teil 1 behandelt die erforderlichen Theorien, beschränkt sich aber nicht auf theoretische Grundlagen, sondern bietet immer auch praktisch erprobte Schaltungen für konkrete Projekte. Zahlreiche Schaltungen können zum Ausgangspunkt für eigene Entwicklungen werden.
Es wurde versucht, einen umfassenden Überblick der wichtigsten Bereiche zu geben. Viele in der praktischen Arbeit auftretende Probleme führen dazu, dass man häufig auf der Suche nach konkreten Fachinformationen ist. Die Zusammenstellung der Inhalte wurde daher auch von dem Ziel geleitet, die Suche nach praktisch relevanten Informationen zu vereinfachen.
Ich wünsche allen Lesern viel Erfolg bei der praktischen Arbeit mit dem Analogteil des Buches!
Burkhard Kainka
1 Einleitung
2 Der Gleichstromkreis
2.1 Ladung und Strom
2.2 Leistung und Spannung
2.3 Der elektrische Widerstand, Ohmsches Gesetz
2.4 Drahtwiderstand
2.5 Reihenschaltung
2.6 Parallelschaltung
2.7 Vorwiderstände
2.8 Innenwiderstand
3 Der Wechselstromkreis
3.1 Effektivspannung und Leistung
3.2 Das Dezibel
3.3 Transformatoren
3.4 Kondensatoren
3.5 RC-Glieder
3.6 Kondensator-Bauformen
3.7 Induktivitäten
3.8 Spulen-Bauformen
3.9 Schwingkreise
4 Dioden-Sperrschichten
4.1 Leitfähigkeit und Dotierung
4.2 Die Diode
4.3 Anwendung der Diode als Gleichrichter
4.4 Dioden-Kennlinien
4.5 Dioden-Bauformen
5 Der bipolare Transistor
5.1 Aufbau und Grundfunktion
5.2 Der Stromverstärkungsfaktor
5.3 Transistor-Kennlinien
5.4 Transistor-Bauformen
6 Feldeffekttransistoren
6.1 Der J-FET
6.2 Doppelgate-MOS-FET
6.3 VMOS-Leistungstransistoren
7 Verstärker-Grundschaltungen
7.1 Der Verstärker in Emitterschaltung
7.2 Gegenkopplung
7.3 Steilheit und Innenwiderstand
7.4 Breitbandverstärker
7.5 Gleichstromgekoppelte Stufen
7.6 Die Kollektorschaltung (Der Emitterfolger)
7.7 Die Basisschaltung
7.8 Die Darlington-Schaltung
7.9 Der Differenzverstärker
7.10 Der Gegentaktverstärker
7.11 Die Konstantstromquelle
8 Transistor-Kippstufen
8.1 Statische Flip-Flops
8.2 Monoflops
8.3 Schmitt-Trigger
9 Transistor-Oszillatoren
9.1 Der Multivibrator
9.2 RC-Oszillatoren
9.3 LC-Oszillatoren
10 Operationsverstärker
10.1 Prinzipschaltung
10.2 Der OPV als Komparator
10.3 OPV-Grundschaltungen
10.4 Invertierende Verstärker
10.5 OPVs mit einfacher Spannungsversorgung
10.6 NF-Vorverstärker
10.7 Leistungsverstärker
10.8 Feldeffekt-OPV
10.9 Der OTA
11 Hochfrequenz-Anwendungen
11.1 Modulation und Demodulation
11.2 Das Diodenradio
11.3 Das Audion
11.4 UKW-Pendelaudion
11.5 HF-Oszillatoren
12 Stromversorgungen
12.1 Batterieversorgung
12.2 Netzteil-Grundschaltungen
12.3 Spannungs-Vervielfachung
12.4 Spannungsstabilisierung mit Z-Dioden
12.5 Längsregler
12.6 Integrierte Spannungsregler
12.7 Bandgap-Referenzen
12.8 Entkopplung der Spannungsversorgung
13 Spannungswandler und Schaltnetzteile
13.1 Spannungswandler
13.2 Schaltregler
13.3 Spannungswandler mit geschalteten Kondensatoren
14 Messtechnik
14.1 Messbereichserweiterungen beim Voltmeter
14.2 Messbereichserweiterung beim Amperemeter
14.3 Das Ohmmeter
14.4 Messfehler
14.5 Messgleichrichter
14.6 Logarithmierer
14.7 Messbrücken
15 Signalgeneratoren
15.1 Rechteck-Generatoren mit OPV
15.2 Rechteckgenerator mit dem 555
15.3 CMOS-Oszillatoren
15.4 Wien-Brücken-Oszillator
15.5 Integrierte Funktionsgeneratoren
15.6 Spannungsgesteuerte Oszillatoren
15.7 Steuerbarer Sinusgenerator mit OTA
16 Sensoren
16.1 NTC-Sensoren
16.2 PT100-Messwiderstände
16.3 KTY-Sensoren
16.4 Dioden und Transistoren als Temperatursensoren
16.5 Integrierte Temperatursensoren
16.6 Thermoelemente
16.7 Lichtsensoren: LDR
16.8 Fotodioden und Fototransistoren
16.9 Kraftsensoren und Drucksensoren
16.10 Piezo-Sensoren
16.11 Magnetfeld-Sensoren
17 Leistungselektronik
17.1 Lineare Leistungsregler
17.2 Leistungsschalter
17.3 Leistungs-MOS-FETs
17.4 PWM-Regler
17.5 Integrierte Leistungsschalter
17.6 Brückentreiber
17.7 Power-OPV
18 Filter
18.1 Entstörmaßnahmen
18.2 Passive RC-Filter
18.3 LC-Filter
18.4 Quarzfilter
18.5 Aktive Filter
18.6 Universalfilter
18.7 Spannungsgesteuerte Filter
19 Mischer und Modulatoren
19.1 Empfängerkonzepte
19.2 Multiplikative Mischer
19.3 Additive Mischer
19.4 Ringmischer
19.5 Integrierte Balance-Mischer
Literatur
Sachverzeichnis
Wer sich ernsthaft mit der Elektronik auseinandersetzen möchte, muss sich die Frage stellen: Welche Voraussetzungen sind erforderlich, um erfolgreich und selbständig arbeiten zu können?
Wichtig sind zunächst solide Kenntnisse der Grundlagen des elektrischen Stromkreises. Nützlich sind lebendige und bildhafte Vorstellungen der Grundphänomene Ladung, Strom, Spannung. Wer in komplexen Schaltungen den Überblick behalten will, der muss sehen lernen, was eigentlich unsichtbar ist. Damit verbunden ist der sichere Gebrauch von Messgeräten. Hinzu kommt das Verständnis der grundlegenden passiven Bauteile, wie Widerstände und Kondensatoren, und ihrer Eigenschaften. Ebenso sollte man sich klare Vorstellungen von Halbleitern und Sperrschichten erarbeiten, um ihr Verhalten in konkreten Schaltungen zu verstehen. Die ersten Kapitel geben einen Überblick und helfen bei der Orientierung. Wer hier schon allzu Bekanntes findet, kann sich gleich in die konkrete Schaltungstechnik der darauffolgenden Kapitel vertiefen.
Obwohl es eine unübersehbar große Zahl unterschiedlicher Schaltungen gibt, lassen sich einige wenige Grundschaltungen angeben, die in jeweils anderen Zusammenhängen immer wieder vorkommen. Die wichtigsten sollte man praktisch erproben und möglichst genau untersuchen. Es lohnt sich, eigene Projekte zu entwerfen und aus einfachen Grundschaltungen zusammenzusetzen. In einer komplexen Schaltung sollte man typische Grundschaltungen wiedererkennen, um die Funktion der Gesamtschaltung zu überblicken. Dies ist eine wichtige Voraussetzung für das Verständnis weiterführender Literatur.
Nicht alles funktioniert auf Anhieb so reibungslos wie man es sich wünschen würde. Wichtig ist daher das Verständnis möglicher Probleme und Grenzfälle. Bei der Planung einer Schaltung müssen mögliche Bauteiletoleranzen und ihre Auswirkungen bedacht werden. Die Zuverlässigkeit eines Geräts hängt oft davon ab, ob Grenzwerte richtig eingeschätzt wurden. Oft gibt es unerwünschte Nebeneffekte, die zu Überraschungen führen können. Das sichere Erkennen möglicher Fehlerquellen setzt einige Erfahrungen voraus. Teil 1 des Buches versucht einen Grundschatz an Erfahrungen für die praktische Arbeit zu vermitteln, damit auftretende Probleme gelöst werden können. Allerdings ist der Lernprozess niemals wirklich abgeschlossen, denn in der praktischen Arbeit müssen laufend neue Probleme gelöst werden.
Wer sich auf fertig entwickelte Schaltungen aus Zeitschriften oder Büchern beschränkt, hat selten Probleme. Richtig interessant wird es aber erst, wenn man eigene Projekte realisiert. Der entscheidende Punkt ist dabei die Auswahl geeigneter Bauteile. Besonders im Bereich der integrierten Schaltungen gibt es eine unüberschaubare Vielfalt. Wichtig ist daher die Fähigkeit, Datenblätter der Hersteller zu lesen und zu interpretieren. Einige der wichtigsten Bauteile werden an Hand von Auszügen aus Datenblättern genauer vorgestellt, um zu zeigen, worauf es im einzelnen ankommt. Oft geben auch die Innenschaltungen integrierter Schaltungen entscheidende Hinweise für den Einsatz.
Bei der Entwicklung elektronischer Schaltungen kommt man nicht ganz ohne mathematische Grundkenntnisse aus. Im Prinzip kann man zu jeder Schaltung ein geeignetes mathematisches Modell suchen, das sie vollständig beschreibt. In der Praxis reichen jedoch einige wenige einfache Berechnungen. In vielen Fällen ist es ebenso wichtig, einfache Abschätzungen und Überschlagsrechnungen vorzunehmen. Oft reicht es, von gegebenen Schaltungen auszugehen und mit einfachen Umrechnungen auf den gewünschten Fall zu schließen. Es wird versucht mit einem Minimum an Mathematik auszukommen. Es werden nur die wichtigsten und für die Praxis relevanten Berechnungen vorgestellt.
Wer elektronische Schaltungen entwerfen möchte, sollte einiges über die Gesetze des Stromkreises wissen. Vieles kann mit geringem Aufwand berechnet werden, wenn man die richtigen Formeln zur Hand hat. Dieses Kapitel will die wichtigsten Gesetze und Formeln vorstellen und zugleich einige grundlegenden Prinzipien für den Entwurf elektronischer Schaltungen vermitteln.
Die grundlegende Größe der Elektrizitätslehre ist die elektrische Ladung Q. Sie wird in Coulomb (C) gemessen. Ein Coulomb ist etwa soviel Ladung, wie in zehn Sekunden durch eine kleine Glühlampe fließt. Jedes Elektron und jeder Atomkern besitzen eine bestimmte, sehr kleine Ladung. Ein Elektron hat die Ladung Q=1,6*10-19 C (0,00000000000000000016 C). An elektrischen Vorgängen sind daher immer sehr viele Elektronen beteiligt.
Der elektrische Strom ist eine Bewegung elektrischer Ladung. Man kann daher die Frage stellen: Wieviel Ladung Q bewegt sich in einer bestimmten Zeit t durch einen Draht. Wenn viel Ladung in kurzer Zeit fließt, beobachtet man einen großen Strom. Die Stromstärke I wird daher so definiert:
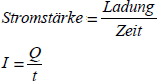
Die Stromstärke I wird in Ampere (A) gemessen. Kleinere Ströme misst man in Milliampere (mA). 1000 mA ist gleich 1 A. Noch viel kleinere Ströme gibt man in Mikroampere (µA) an. 1000 µA = 1 mA.
Bei der Messung der Stromstärke liegt das Messgerät nach Abb. 2.1 immer in Reihe zum Verbraucher. Der gesamte Strom fließt durch das Amperemeter und ruft dort eine Wirkung hervor, indem er z.B. über den Umweg über magnetische Kräfte einen Zeiger bewegt. Das ideale Amperemeter beeinflusst den Stromkreis selbst nicht, weil es selbst einen sehr geringen Widerstand besitzt, sich also annähernd so verhält wie ein einfaches Kabel. Das bedeutet zugleich, dass man sehr vorsichtig sein muss, das Amperemeter niemals versehentlich parallel zur Spannungsquelle anzuschließen, denn das bedeutete einen Kurzschluss.
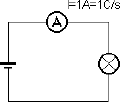
Abb. 2.1 Strom und Ladung im Stromkreis
Meist ist es einfacher die Stromstärke zu messen als die Ladung. Man kann die Ladung aus der Stromstärke und der Zeit berechnen, indem man die obige Formel umstellt. Es soll z.B. berechnet werden, welche Ladung insgesamt von einer Akkuzelle mit den Daten 1,2 V/500 mAh bewegt werden kann. Ein Strom von 0,5 A wird eine Stunde lang, also für 3600 Sekunden aufrechterhalten. In dieser Zeit bewegt sich die Ladung:
Q = I · t
Q = 0,5 A · 3600s
Q = 1800C
Für die gesamte Ladung von 1800 C müssen etwa 1022 Elektronen bewegt werden.
Die elektrischen Messgrößen hängen auch mit den Größen anderer physikalischer Fachbereiche zusammen. So wird z.B. die Einheit der Leistung, das Watt (W), an mechanischen Vorgängen definiert. Wenn man einen Gegenstand von einem Kilogramm gegen die Schwerkraft der Erde in zehn Sekunden um einen Meter anhebt, dann benötigt man dazu eine Leistung von ca. einem Watt. Die genaue Definition lautet: Leistung = Kraft * Weg / Zeit, die Einheit ist definiert als 1 Watt = 1 Newton * 1 Meter / 1 Sekunde. Bei einer Gewichtskraft von 9,81 N würde für das Anheben tatsächlich eine Leistung von 0,981 W benötigt. Setzt man dazu einen Elektromotor ein, wird eine elektrische Leistung von ebenfalls etwa einem Watt benötigt, oder etwas mehr, weil der Motor nebenbei auch Wärme erzeugt. Ein Motor mit der Leistung 100 Watt könnte entsprechend mehr in kürzerer Zeit heben.
Die messbare Leistung eines elektrischen Geräts hängt von der elektrischen Stromstärke I und der elektrischen Spannung U ab (vgl. Abb. 2.2). Eine größere Spannung bedeutet, dass bei gleichem Strom mehr Leistung umgesetzt wird. Man kann daher die Spannung als abgeleitete Größe definieren:
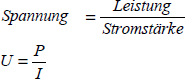
Umgekehrt lässt sich die elektrische Leistung berechnen, wenn Spannung und Stromstärke gemessen wurden. An einer Glühlampe wurde z.B. gemessen: U = 6 V, I = 0,4 A. Die Leistung beträgt dann:
P = U · I
P = 6V · 0,4 A
P = 2,4W
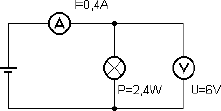
Abb. 2.2 Messung der Leistung
Diese Lampe mit der Leistung 2,4 W wird im Scheinwerfer eines Fahrrads eingesetzt. Sie ist wesentlich heller als die Rücklichtlampe mit der Leistung 0,6 W. Allgemein kann man sagen, dass mehr Leistung auch mehr Licht, mehr Wärme oder mehr Bewegung bedeutet. Viel Leistung kann durch eine hohe Spannung oder durch einen großen Strom erreicht werden. Lampen gleicher Leistung können also für unterschiedliche Spannungen ausgelegt werden.
Die elektrische Spannung wird auch als Potentialunterschied zwischen zwei Punkten einer Schaltung definiert, also z.B. zwischen den beiden Anschlüssen einer Batterie. Das elektrische Potential ist definiert als Arbeit geteilt durch Ladung, gibt also an, wieviel Arbeit eine Ladung auf einem Weg verrichtet. Dazu muss ein willkürlicher Nullpunkt festgelegt werden, wozu meist die Erde verwendet wird. Eine gegen Erde gemessene Spannung kann daher auch als Potential bezeichnet werden. In elektronischen Schaltungen verwendet man oft eine Masseleitung (oft der Minusanschluss der Spannungsversorgung) als Bezugspunkt, wobei offen bleibt, ob sie tatsächlich geerdet ist. Einige Geräte werden über den Schutzleiter der Steckdose mit Erde verbunden.

Abb. 2.3 Spannungs- und Potenzialangaben in einer Schaltung
Spannungen werden immer zwischen zwei Punkten gemessen. Deshalb bestimmt man die Spannung einer Stromquelle durch Parallelschaltung des Voltmeters. Wenn in einer Schaltung eine Spannung an einem Punkt angegeben ist, ist immer das Potenzial, also die Spannung gegenüber der gemeinsamen Masseleitung gemeint. Der Minusanschluss des Voltmeters liegt dann also an Masse. Das ideale Voltmeter ist extrem hochohmig, es fließt also nur ein vernachlässigbar kleiner Strom durch das Messgerät.
Welcher Strom in einem Stromkreis fließt, hängt einerseits von der elektrischen Spannung der Batterie ab, andererseits aber auch vom eingesetzten Verbraucher, genauer gesagt von seinem elektrischen Widerstand. Der Widerstand ist eine Eigenschaft des Verbrauchers, die man als seine Fähigkeit umschreiben kann, die schnelle Bewegung der elektrischen Ladung zu behindern. Mehr Widerstand bedeutet also bei gleicher Spannung, dass weniger Strom fließt. Der Widerstand R ist als abgeleitete Größe aus Spannung U und Stromstärke I definiert.
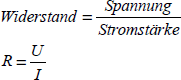
Die Einheit des elektrischen Widerstands ist Ohm (Ω). Ein Ohm ist gleich ein Volt geteilt durch ein Ampere. Der Widerstand einer Glühlampe mit U = 6 V und I = 0,4 A kann also leicht berechnet werden:
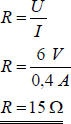
Der Widerstand von 15 Ohm wird allerdings nur bei der vollen Spannung von 6 V gemessen. Bei kleineren Spannungen findet man weniger Widerstand, weil der Widerstand eines Metalldrahts von seiner Temperatur abhängt. Im kalten Zustand hat die Lampe nur etwa 1,5 Ω.
In der Elektronik verwendet man Widerstände als kleine, kompakte Bauteile in der Form von Kohleschicht-, Metallschicht- oder Drahtwiderständen. Diese Widerstände besitzen einen sehr konstanten elektrischen Widerstand, der als Zahl oder in Form von Farbringen aufgedruckt ist. Man findet Werte zwischen ca. 1 Ω, 1 kΩ (Kiloohm, 1000 Ω) und 1 MΩ (Megaohm, 1000000 Ω). Legt man einen Widerstand an eine bekannte Spannung, dann ist der Strom leicht zu berechnen. Ein Widerstand mit 4,7 kΩ soll z.B. an 6 V liegen (vgl. Abb. 2.4). Die Stromstärke ist dann:
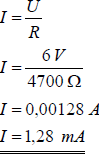
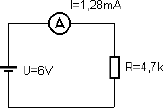
Abb. 2.4 Ein Widerstand im Stromkreis
Meist werden Widerstände jedoch nicht allein verwendet, sondern zusammen mit anderen Bauelementen. So benötigt man z.B. einen Vorwiderstand zum Betrieb einer Leuchtdiode (LED). Die Größe des Widerstands kann leicht berechnet werden, wenn man die gewünschte Stromstärke und die Spannung am Widerstand kennt.
Als Bauteile für elektronische Schaltungen werden Widerstände meist als Kohleschichtwiderstände mit Toleranzen von ±5% oder als Metallschichtwiderstände mit Toleranzen von ±1% gefertigt, wobei das Widerstandsmaterial auf einen Keramikstab aufgebracht und mit einer Schutzschicht überzogen ist. Die Beschriftung erfolgt meist in Form von Farbringen. Kohleschichtwiderstände verwenden drei Farbringe, Metallschichtwiderstände vier. Neben dem Widerstandswert ist auch die Genauigkeitsklasse in Prozent angegeben.
Widerstände mit einer Toleranz von ±5% gibt es in den Werten der E24-Reihe, wobei jede Dekade 24 Werte mit etwa gleichmäßigem Abstand zum Nachbarwert enthält.
Tabelle 2.1 Widerstandswerte nach der Normreihe E24

Berechnet man für eine Schaltung einen Widerstand von 5 kΩ, dann muss entsprechend der Normreihe entweder 4,7 kΩ oder 5,1 kΩ verwendet werden. Oft steht sogar nur die E12-Reihe zur Verfügung, in der jeder zweite Wert fehlt. Dann wird man entweder 4,7 kΩ oder 5,6 kΩ wählen. Wenn es auf engere Toleranzen ankommt, sollte man Metallschichtwiderstände verwenden, die meist mit einer Genauigkeit von 1% und in den Werten der Normreihe E96 geliefert werden.
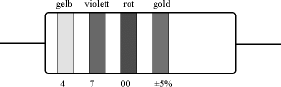
Abb. 2.5 Farbcodierung von Widerständen
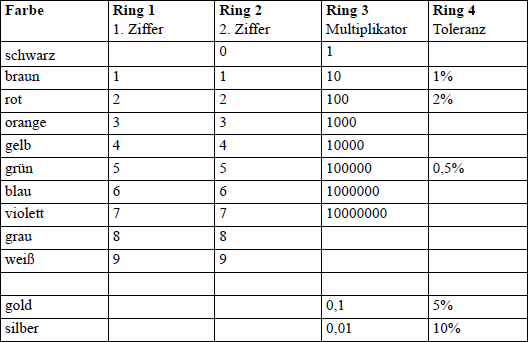
Der Farbcode wird ausgehend von dem Ring gelesen, der näher am Rand des Widerstands liegt. Bei drei Ringen stehen die beiden ersten für zwei Ziffern, der dritte für einen Multiplikator für den Widerstandswert in Ohm. Ein vierter Ring gibt die Toleranz an.
Tabelle 2.2 Der Widerstands-Farbcode
Ein Widerstand mit den Farbringen gelb, violett, rot und gold hat den Wert 4700 Ohm oder 4,7 Kiloohm bei einer Toleranz von 5%. Widerstände der Normreihe E96 benötigen eine Ziffer mehr und haben daher insgesamt fünf Ringe. Für den gleichen Wert von 4700 Ω lautet die Farbcodierung nun gelb, violett, schwarz und braun, mit einem zusätzlichen braunen Ring für die Toleranz 1%.
Wichtig ist auch die maximale Belastbarkeit. Kleine Widerstände dürfen z.B. bis zu 1/8 Watt oder 1/4 Watt aufnehmen. Überlastung führt zur Überhitzung des Widerstands. Bei längerer und erheblicher Überlastung wird der Widerstand zerstört. Er wird dabei in den meisten Fällen hochohmig, weil die Widerstandsschicht verbrennt.
Jeder Metalldraht hat einen elektrischen Widerstand. In vielen Fällen kann man den Drahtwiderstand vernachlässigen, weil ausreichend dicke und kurze Drähte von einem so kleinen Strom durchflossen werden, dass kein merklicher Spannungsabfall auftritt. Wenn allerdings kleinste Spannungsabfälle stören, wenn sehr lange Leitungen verwendet werden müssen oder zur Bestimmung des Widerstands von Spulen und Transformatoren, muss der Drahtwiderstand bedacht werden. In anderen Fällen möchte man gerade einen ganz bestimmten Widerstand durch ein Stück Draht realisieren, z.B. für einen Messwiderstand für erhöhte Strombelastung. In all diesen Fällen ist es wichtig, den Drahtwiderstand bestimmen zu können.
Der Widerstand eines Drahts hängt von seiner Länge, seiner Querschnittsfläche, dem verwendeten Metall und der Temperatur ab. Für jedes Metall kann ein spezifischer Widerstand ρ (griech. Rho) in Ω*m (aus Ω*m2/m) angegeben werden. Ein Draht hat dann den Widerstand
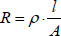
l = Länge in m
A = Querschnitt in m2
Der spezifische Widerstand wird meist für eine Temperatur von 20 °C angegeben. Bei den meisten nicht legierten Metallen steigt der Widerstand um ca. 0,4% pro Grad an. Die Tabelle 2.3 zeigt den spezifischen Widerstand und den Temperaturkoeffizienten für einige in der Elektronik wichtige Metalle.
Der spezifische Widerstand von Metallen wurde früher meist in Ω*mm2/m angegeben. Heute werden allgemein die Einheiten Meter und Quadratmeter verwendet. Für einen Kupferdraht der Länge 1 m und des Durchmessers 0,2 mm ergibt sich mit A = r2π folgender Widerstand:
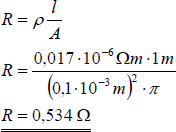
Tabelle 2.3 Spezifische Widerstände einiger Metalle
| Metall | r in 10-6 Ωm bei 20 °C | TK in 10-3/K |
| Kupfer | 0,017 | 4,33 |
| Silber | 0,015 | 4,1 |
| Eisen | 0,10 | 5,6 |
| Wolfram | 0,049 | 4,8 |
| Platin | 0,089 | 3,92 |
| Konstantan | 0,50 | -0,03 |
Ein Widerstand von 0,5 Ω ist meist nicht mehr zu vernachlässigen. Dazu kommt der positive Temperaturkoeffizient des Kupfers von 0,433 %/K. Bei 100 °C hätte der gleiche Draht bereits einen Widerstand von mehr als 0,7 Ω. Die elektrischen Verluste in Drähten erhöhen sich daher mit steigender Temperatur. Andererseits kann man die Temperaturabhängigkeit des Widerstands zur Kompensation von Temperatureffekten in elektronischen Schaltungen einsetzen oder gezielt für Messzwecke ausnutzen.
Speziell für hochgenaue Temperaturmessungen verwendet man abgeglichene Platin-Messwiderstände z.B. mit 100 Ω bei 0 °C, so genannte Pt-100-Sensoren. Mit ähnlichem Ergebnis könnte man aber auch Kupfer oder Wolfram zur Temperaturmessung einsetzen. Eine Kupferspule oder eine hochohmige Glühlampe in Verbindung mit einem Ohmmeter kann also durchaus zur Temperaturmessung verwendet werden.
Wenn es auf größtmögliche Temperaturunabhängigkeit ankommt, verwendet man gern Konstantan, eine Legierung aus 54% Kupfer, 45% Nickel und 1% Mangan. Der Temperaturkoeffizient liegt nahe Null. Für sehr niederohmige Messwiderstände kann es sinnvoll sein, kurze Drahtstücke aus Konstantan zu verwenden. Der genaue Widerstand kann über die Drahtlänge abgeglichen werden. In Messgeräten mit einem großen Strom-Messbereich von z.B. 10 A findet man oft Messwiderstände aus einer kurzen und dicken Drahtbrücke.
In Glühlampen verwendet man Glühdrähte aus Wolfram, weil dieses Metall einen extrem hohen Schmelzpunkt von 3380 °C besitzt. Die normale Arbeitstemperatur bei angeschalteter Glühlampe liegt bei ca. 2200 °C. Bei dieser Temperatur erreicht der Glühfaden den zehnfachen Kaltwiderstand. So hat z.B. eine Glühlampe von 12 V/0,1 A einen Arbeitswiderstand von 120 Ω und damit einen Kaltwiderstand von 12 Ω. Man kann diese Information benutzen, um eine unbekannte Glühlampe über ihren Kaltwiderstand zu identifizieren. Zum anderen ist es oft wichtig zu bedenken, dass die Glühlampe beim Einschalten wegen des zehnfach geringeren Kaltwiderstands einen Stromstoß vom Zehnfachen des Nennstroms verursacht. Dieser kann bei falscher Dimensionierung einer Schaltung z.B. einen Schalttransistor überlasten.
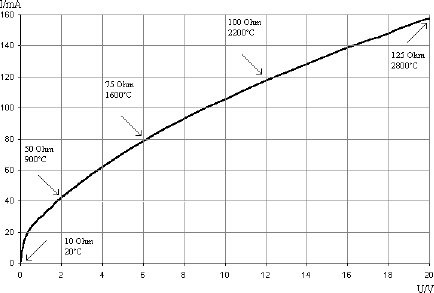
Abb. 2.6 Die Kennlinie einer 12-V-Glühlampe
Abb. 2.6 zeigt die U/I-Kennlinie einer Glühlampe mit eingezeichneten Widerstands- und Temperaturpunkten. Die Kennlinie geht im Bereich der Nennspannung in einen Bereich relativ konstanten Stroms über. Jede Erhöhung der Spannung führt nämlich zu einer Temperaturerhöhung des Glühfadens und damit zu einer Widerstandserhöhung, die der stärkeren Erhöhung des Stroms entgegenwirkt. Eine Erhöhung der Spannung um 10% vergrößert den Strom nur um ca. 5%. Dieses PTC-Verhalten (positiver Temperaturkoeffizient) kann verwendet werden, wenn es auf eine Stabilisierung des Stroms ankommt. Eine geeignete Glühlampe als Vorwiderstand in einem Akku-Ladegerät führt zu einem relativ konstanten Ladestrom über die gesamte Ladedauer.
Der Ladevorgang beginnt bei einem entladenen dreizelligen NiCd-Akku nach Abb. 2.7 mit einer Ladespannung von z.B. 3 V, so dass 6 V an der Lampe liegen. Gegen Ende der Ladung steigt die Akkuspannung im Anwendungsbeispiel bis auf ca. 4,5 V an, die Spannung an der Glühlampe fällt auf 4,5 V. Der Strom fällt aber nur unwesentlich unter 100 mA ab, so dass man die Ladedauer grob auf fünf Stunden festlegen kann. Bei einem Festwiderstand müsste man dagegen den Stromabfall gegen Ende der Ladezeit berücksichtigen. Weitere Vorteile der Glühlampe gegenüber einem Widerstand sind die problemlose Abfuhr der Verlustwärme und die gleichzeitige Anzeige des Ladevorgangs. Eine Glühlampe als Vorwiderstand wird also sinnvoll eingesetzt, um einen kleinen Akku an einem Netzteil zu laden. Bei sehr großen Ladeströmen ist dagegen eine elektronische Ladeschaltung sinnvoll.
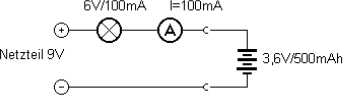
Abb. 2.7 Glühlampe zur Stromstabilisierung in einem Ladegerät
Ein weiterer Einsatz für Glühlampen liegt in der Verwendung als Überstromsicherung. Der abgesicherte Strom sollte dabei möglichst weit unterhalb des Nennstroms der Glühlampe liegen, damit nur ein kleiner Spannungsabfall auftritt. Im Kurzschlussfall wird der Strom aber etwa auf den Nennstrom begrenzt. Die Glühlampe kann damit relativ einfach experimentelle Schaltungen absichern. Ein verbesserter Ersatz für die Glühlampe sind sog. Polyswitch-Sicherungen in Form von speziellen PTC-Widerständen.
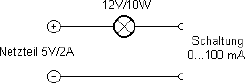
Abb. 2.8 Glühlampe als Sicherungsersatz
Im Anwendungsbeispiel nach Abb. 2.8 wird eine relativ kleine Schaltung mit einem Strombedarf bis 100 mA an einem kräftigen Netzteil bis 2 A betrieben. Im Kurzschlussfall wird der Strom sicher auf weit unter 1 A begrenzt. Damit ist sowohl eine Beschädigung des Netzteils als auch eine mögliche Brandgefahr ausgeschlossen. Im normalen Betrieb fällt dagegen am Kaltwiderstand der Glühlampe von ca. 1,5 Ω nur eine Spannung von max. 0,15 V ab. Gegenüber einer normalen Sicherung hat man den Vorteil, dass die Glühlampe nach einem Kurzschluss nicht ausgewechselt werden muss. Gerade bei der experimentellen Arbeit bringt dies erhebliche Vorteile. So kann man z.B. das Netzteil eines Computers gefahrlos für kleine Schaltungen mit verwenden.
Schaltet man zwei Verbraucher, also z.B. zwei Widerstände, in Reihe, dann fließt durch beide derselbe Strom. Es gibt nur einen Stromweg. Deshalb spricht man hier auch vom unverzweigten Stromkreis. Die Stromstärke hängt vom Gesamtwiderstand ab. Der Gesamtwiderstand ist die Summe aller Teilwiderstände.
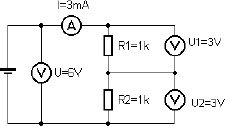
Abb. 2.9 Die Reihenschaltung
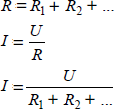
Die Spannung teilt sich in Reihenschaltung auf alle Verbraucher auf. Die Spannung (man spricht hier auch vom „Spannungsabfall“) an einem Widerstand kann leicht aus der Stromstärke bestimmt werden.
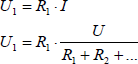
Bei gleichen Widerständen teilt sich die Spannung in gleiche Teile auf. Oft findet man ungleiche Widerstände vor. Da praktisch jeder Draht Widerstand hat, gibt es auch im Draht Spannungsabfälle, die z.B. bemerkbar werden, wenn man sehr lange und zu dünne Kabel bei großer Stromstärke verwendet. Abb. 2.10 zeigt einen Reihenstromkreis mit drei unterschiedlichen Widerständen. Die Gesamtspannung teilt sich im Verhältnis der Einzelwiderstände in Teilspannungen.
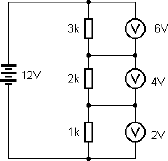
Abb. 2.10 Ein Spannungsteiler mit drei Teilwiderständen
Die Reihenschaltung wird oft auch als Spannungsteiler bezeichnet. Um eine Spannung beliebig zu teilen, setzt man Potentiometer ein. Potentiometer sind Widerstände mit einem verstellbaren Abgriff. Meist verwendet man eine kreisförmige Widerstandsbahn (vgl. Abb. 2.11) und einen Schleifer aus Metall oder Graphit. Man setzt sie z.B. als Lautstärkeregler ein. Jedes Poti stellt einen variablen Spannungsteiler dar. Potentiometer ohne Achse, die sich mit einem Schraubendreher verstellen lassen, bezeichnet man auch als Trimmer.
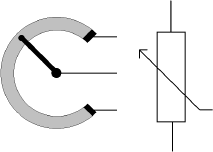
Abb. 2.11 Prinzip des Potentiometers
Bei der Parallelschaltung mehrerer Verbraucher oder Widerstände entstehen mehrere Stromzweige mit jeweils unterschiedlichen Stromstärken. Der Gesamtstrom verzweigt sich in Teilströme. Man bezeichnet die Parallelschaltung daher auch als den verzweigten Stromkreis.
Bei der Parallelschaltung mehrerer Verbraucher addieren sich die Ströme, während die Spannung an jedem Verbraucher die gleiche ist. Für den Gesamtstrom gilt:
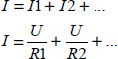
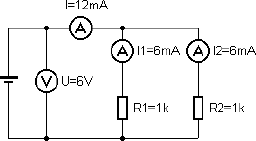
Abb. 2.12 Die Parallelschaltung
In der Beispielschaltung nach Abb. 2.12 findet man zwei Teilströme mit jeweils 6 mA. Beide Widerstände mit jeweils 1000 Ω könnten durch einen Widerstand mit 500 Ω ersetzt werden (Ersatzwiderstand), um denselben Gesamtstrom von 12 mA zu erreichen. Zwei gleiche Widerstände in Parallelschaltung ersetzen also einen halb so großen Widerstand. Oft möchte man einen Widerstand durch mehrere Widerstände ersetzen, z.B. um die erlaubte Verlustleistung zu erhöhen. Zehn Widerstände mit 1 Ω/0,25 W in Parallelschaltung ersetzen einen Leistungswiderstand mit 0,1 Ω/2,5 W. Allgemein kann man für mehrere parallele Widerstände R1, R2, R3 usw. einen Ersatzwiderstand R angeben.
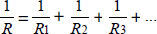
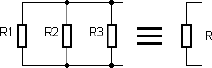
Abb. 2.13 Ersetzen eines Widerstands durch eine Parallelschaltung
Will man die Spannung an einem Verbraucher verkleinern, dann kann man einen Widerstand in Reihe als „Vorwiderstand“ einsetzen. Der Spannungsabfall am Vorwiderstand verkleinert die Spannung am Verbraucher. Soll z.B. eine Glühlampe mit 6 V/0,1 A an 9 V betrieben werden, dann muss der Vorwiderstand einen Spannungsabfall von 3 V aufnehmen. Der Strom durch den Vorwiderstand ist wegen der Reihenschaltung ebenfalls 0,1 A. Der passende Widerstand kann also leicht berechnet werden.
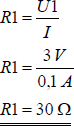
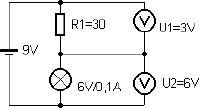
Abb. 2.14 Verwendung eines Vorwiderstands
Für Leuchtdioden (LEDs) müssen prinzipiell Vorwiderstände eingesetzt werden, weil sie nicht bei einer bestimmten Spannung, sondern mit einem definierten Strom von max. 20 mA betrieben werden sollen. Die Anschlussspannung beträgt dabei je nach Typ zwischen 1,5 V und 2 V. Für eine rote LED kann man z.B. von 1,5 V ausgehen. Der Vorwiderstand muss die restliche Spannung aufnehmen, also z.B. 4,5 V an einer Batteriespannung von 6 V. Man berechnet in diesem Fall einen Widerstand von 225 Ω.
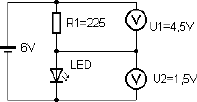
Abb. 2.15 Ein Vorwiderstand für eine Leuchtdiode
Jede Batterie und die meisten Netzteile zeigen einen deutlichen Spannungsabfall, wenn ein Verbraucher eingeschaltet wird. So kann z.B. die Spannung einer Flachbatterie beim Anschluss einer Glühlampe mit 0,3 A von 4,5 V um 0,6 V auf 3,9 V abfallen. Man kann sich die Batterie als eine Reihenschaltung aus einer idealen, also sehr konstanten Spannungsquelle mit 4,5 V und einem Widerstand vorstellen. Dieser gedachte Vorwiderstand hat in diesem Fall 2 Ohm.
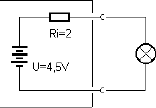
Abb. 2.16 Der Innenwiderstand einer Batterie
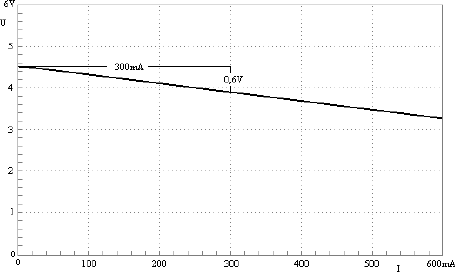
Abb. 2.17 Abnahme der Anschlussspannung mit zunehmendem Strom
Allgemein kann man den Innenwiderstand Ri einer Stromquelle bestimmen, indem man die Spannung bei zwei unterschiedlichen Stromstärken misst. Abb. 2.17 zeigt ein typisches Messergebnis. Der Spannungsunterschied ΔU (sprich: Delta-U) bei einem Stromstärkenunterschied ΔI erlaubt die Berechnung des Innenwiderstands Ri.
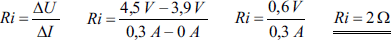
Praktisch alle Spannungsquellen wie Batterien, Transformatoren, Mikrofone, Antennen und Verstärker haben einen bestimmten Innenwiderstand. Man muss seinen Wert kennen, um den richtigen Verbraucher anzuschließen. Für eine Batterie gilt: Der Widerstand des Verbrauchers sollte sehr viel größer als der Innenwiderstand sein, damit geringe Verluste auftreten. Für Signalquellen wie Mikrofone oder Antennen sollte der Innenwiderstand mit dem Anschlusswiderstand übereinstimmen, weil dann die maximale Leistung abgegeben wird.
Bei einfachen Zink-Kohle- oder Alkalibatterien steigt der Innenwiderstand gegen Ende der Lebensdauer stark an. Er bildet ein gutes Maß zur Beurteilung des Zustands einer Batteriezelle. Die Leerlaufspannung einer Batterie sinkt dagegen kaum ab und ist nur ein unzuverlässiges Kriterium für ihren Zustand. Besonders bei bereits teilweise entladenen Batterien kann statt des Innenwiderstands einfach der Kurzschlussstrom gemessen werden, indem man ein Amperemeter im höchsten Strombereich von z.B. 10 A parallel zur Batterie schaltet.
Ein Kurzschlussstrom von 1 A bedeutet für eine 1,5-V-Batterie einen Innenwiderstand von 1,5 Ω, was für eine einfache Zink-Kohlebatterie noch ein guter Wert ist. Die Kurzschlussmethode bietet sich an, um aus mehreren teilweise entladenen Batterien zuverlässig die besten herauszusuchen. Vorsicht ist allerdings bei relativ neuen Alkalibatterien und bei Akkus geboten, wo leicht mehr als 10 A fließen können. Bei Akkus steigt der Innenwiderstand überdies erst am Ende der Entladeperiode stark an, so dass er kaum eine Aussage über den Ladezustand liefert. Dagegen lassen sich verbrauchte Akkus an einem hohen Innenwiderstand im frisch geladenen Zustand erkennen.
Übliche Batterietester verwenden meist eine Spannungsmessung unter einer für den jeweiligen Batterietyp typischen Belastung im Bereich um 100 mA. Das Messergebnis sagt mehr aus als eine reine Messung der Leerlaufspannung mit einem hochohmigen Voltmeter, weil bei der Belastung der Batterie ein vom Innenwiderstand abhängiger Spannungsabfall auftritt. Genauso vermittelt natürlich auch eine einfache Glühlampe einen Eindruck vom Zustand einer Batterie, wenn ihre Daten einigermaßen zur Anschlussspannung und zum typischen Entladestrom der Batterie passen.
Die Gesetze des Gleichstromkreises gelten grundsätzlich auch für Wechselstrom. Allerdings treten bei Wechselstrom einige zusätzliche Phänomene auf. Insbesondere Kondensatoren und Spulen verhalten sich völlig anders als bei Gleichstrom. Die Grundlagen des Wechselstromkreises spielen in der analogen Schaltungstechnik eine wichtige Rolle, weil vielfach Wechselspannungssignale verarbeitet werden. Außer der Spannung und der Stromstärke muss hier auch die Frequenz und die Kurvenform eines Signals beachtet werden. Während Wechselstromkreise zunächst bei sinusförmigen Wechselspannungen untersucht werden, treten in elektronischen Schaltungen auch Rechteck-, Dreieck- und andere Signale auf.
Während Batterien Gleichstrom liefern, verwendet man im Lichtnetz Wechselstrom. Die Polarität der Wechselspannung kehrt sich mit einer Frequenz f laufend um. An der Steckdose findet man eine Wechselspannung mit 230 V bei einer Frequenz von 50 Hertz (f = 50 Hz), also mit 50 vollständigen Wechseln in einer Sekunde. Eine volle Periode dauert 20 Millisekunden. Die höchste Momentanspannung, also die Spitzenspannung Us, liegt bei ca. 325 V. Die Spitze-Spitze-Spannung Uss beträgt 650 V. Die Effektivspannung Ueff beträgt 230 V. Das bedeutet, dass an einem ohmschen Widerstand bei einer Gleichspannung von 230 V die gleiche mittlere Leistung umgesetzt wird. Mit einem Oszilloskop lässt sich der zeitliche Verlauf der Wechselspannung sichtbar machen.
Die Momentanspannung einer sinusförmigen Wechselspannung folgt allgemein dem Verlauf einer mathematischen Sinusfunktion mit der Höhe Us:
U = Us · sin(2πft)
Mittelt man die auftretenden Leistungen über eine volle Sinusperiode der Wechselspannung, dann zeigt sich, dass die Momentanleistung am Scheitelpunkt Us der Spannung gerade doppelt so groß ist wie die durchschnittliche, also die effektive Leistung. Da die Leistung bei konstantem Widerstand eines Verbrauchers mit dem Quadrat der Spannung steigt, ergibt sich ein Verhältnis zwischen Spitzenspannung Us und Effektivspannung Ueff von √2 = 1,41. Ein Transformator mit einer Sekundärspannung von 12 V liefert also eine Spitzenspannung von 12V * 1,41 = 17 V. Dies spielt eine große Rolle bei der Dimensionierung von Netzteilen.
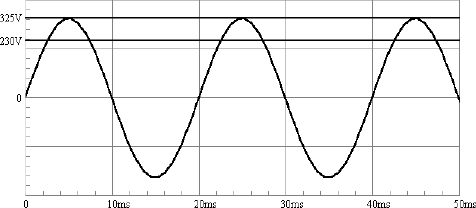
Abb. 3.1 Das Oszillogramm einer Wechselspannung
In der Elektronik verwendet man oft auch rechteckförmige Wechselspannungen. In diesem Fall ist die Effektivspannung gleich der Scheitelspannung. Für jede Kurvenform gilt ein eigenes Verhältnis von Effektivspannung zu Spitzenspannung. Ein Wechselspannungs-Voltmeter zeigt im allgemeinen die Effektivspannung an. Man unterscheidet jedoch zwischen einer echten und technisch sehr aufwendigen Effektivwertmessung (engl. True RMS) und einer nur über die Spannung ermittelten Messung, was bei den einfachen Voltmetern der Fall ist. Diese zeigen nur für sinusförmige Spannungen korrekte Ergebnisse, während bei allen anderen Kurvenformen mehr oder weniger falsche Messwerte angezeigt werden. Andererseits ist der Effektivwert nicht unbedingt immer der interessante Messwert. In der Schaltungstechnik interessiert oft mehr die Spitzenspannung, die sich am besten mit einem Oszilloskop bestimmen lässt.
Jede beliebige periodische Kurvenform lässt sich aus Sinusschwingungen zusammensetzen, wobei eine Grundfrequenz und Vielfache davon verwendet werden. Umgekehrt kann man auch sagen, dass eine beliebige Kurvenform eine Grundschwingung und viele Oberschwingungen enthält. Eine Rechteckspannung mit der Grundfrequenz 100 Hz enthält neben der Grundfrequenz von 100 Hz auch noch schwächere Oberschwingungen mit den Frequenzen 300 Hz, 500 Hz, 700 Hz usw. Legt man eine bestimmte Signalform an einen Lautsprecher, dann ist der Gehalt an Obertönen im Klangbild des Signals deutlich zu hören. Nur der reine Sinuston enthält keine Obertöne. Jede Verzerrung der reinen Sinusform fügt jedoch Anteile höherer Frequenzen hinzu.
Die Tabelle 3.1 zeigt die relativen Anteile der einzelnen Oberschwingungen für die drei wichtigsten Kurvenformen Rechteck (symmetrisch), Dreieck (symmetrisch) und Sägezahn. Bei den symmetrischen Kurvenformen kommen nur ungerade Oberschwingungen vor. Die Dreieckschwingung ist unter den drei Kurvenformen der Sinusschwingung am ähnlichsten und hat daher den geringsten Gehalt an Anteilen höherer Frequenzen. Den höchsten Gehalt an Obertönen hat die Sägezahnschwingung.
Tabelle 3.1 Oberwellenanteile in einigen Kurvenformen

Bei der Betrachtung von Wechselspannungssignalen ist es üblich, von reinen Sinusspannungen auszugehen. Alle anderen Kurvenformen werden als Gemisch von Sinussignalen betrachtet. Umgekehrt lassen sich beliebige Kurvenformen aus Sinussignalen erzeugen. Abb. 3.2 zeigt die Synthese eines Rechtecksignals aus den ersten drei Grundsignalen. Die angenäherte Rechteckspannung folgt hier der folgenden Funktion:
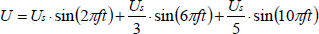
In der Nachrichtentechnik spricht man statt von Spannungen oft von Pegeln. Ein bestimmter Spannungspegel wird auch oft in Dezibel (dB) angegeben. Das Dezibel ist eine reine Verhältnisgröße, d.h., man gibt den Unterschied zu einer Bezugsgröße an. Die Angabe 20 dB bedeutet z.B. die zehnfache Spannung bzw. die 100-fache Leistung. Man kann diese Angabe sinnvoll auf einen Verstärker anwenden und sagen, die Verstärkung beträgt 20 dB. Zur Bestimmung der Verstärkung müssen die Eingangsspannung U1 und die Ausgangsspannung U2 gemessen werden. Die Umrechnung der Verstärkung V in Dezibel beruht auf dem Zehnerlogarithmus des Spannungsverhältnisses:
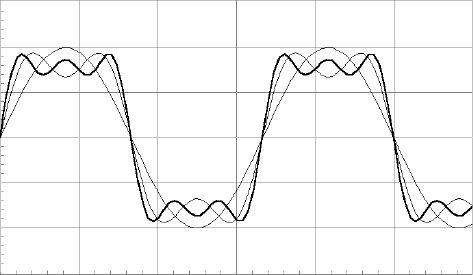
Abb. 3.2 Annäherung eines Rechtecksignals aus drei Sinusspannungen
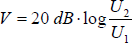
Für eine 100-fache Verstärkung V ergibt sich 40 dB.
V = 20 dB · log100
V = 40 dB
Verwendet man das Dezibel zur Angabe eines Pegels, dann muss immer mit angegeben werden, in Bezug auf welchen Pegel die Angabe gilt. In der Fernmeldetechnik verwendet man z.B. als Bezugspegel 1 mW an 600 Ω. Die Signalspannung beträgt dann 0,7746 V = 0 dBm. Größere oder kleinere Pegel werden in dBm angegeben. Negative Pegel entsprechen kleineren Spannungen, positive größeren.
Als Bezugspegel kommen auch andere Größen in Frage. In der Hochfrequenztechnik verwendet man oft ein Mikrovolt als Nullpegel. Die Angabe 40 dB(µV) bedeutet dann eine Signalspannung von 100 µV.
Tabelle 3.2 Einige Pegel in dBm
| Pegel | Leistung P | Spannung U |
| +20 dBm | 100 mW | 7,75 V |
| +10 dBm | 10 mW | 2,45 V |
| + 3 dBm | ca. 2 mW | 1.10 V |
| 0 dBm | 1 mW | 0,775 V |
| -3 dBm | ca. 0,5 mW | 0,548 V |
| -6 dBm | ca. 0,25 mW | 0,388 V |
| -10 dBm | 0,1 mW | 0,245 V |
| -20 dBm | 0,01 mW | 0,0775 V |
| -30 dBm | 0,001 mW | 0,0245 V |
Ein Vorteil des logarithmischen Maßes dB ist, dass man Abschwächungen und Verstärkungen einfach addieren kann. Zwei hintereinandergeschaltete Verstärker mit Verstärkungen mit jeweils 12 dB haben eine Gesamtverstärkung von 24 dB. Wenn zusätzlich noch ein Leitung mit Verlusten von 2 dB und ein Übertrager mit Verlusten von 4 dB verwendet werden, beträgt die Gesamtverstärkung nur noch 18 dB. Ein weiterer Vorteil ist, dass man sehr große Pegelunterschiede gut zusammen in einem Diagramm darstellen kann.
Der wichtigste Grund Wechselstrom einzusetzen ist die Möglichkeit, mit Transformatoren die Spannung zu verändern. Ein Transformator enthält zwei Drahtspulen auf einem gemeinsamen Eisenkern. Ein Wechselstrom durch eine der Spulen erzeugt ein Magnetfeld im Kern, das in der zweiten Spule eine Spannung induziert. Die Induktion wird weiter unten im Zusammenhang mit Spulen noch genauer erläutert. Das Verhältnis der Windungszahlen eines Transformators entspricht dem Verhältnis der Spannungen. Ein Transformator verändert im umgekehrten Windungsverhältnis die Stromstärke, so dass die Leistung bis auf geringe Verluste unverändert bleibt.
Abb. 3.3 zeigt die Verhältnisse an einem idealen Netztransformator ohne jede Verluste für die Sekundärspannung 12 V. Die Primärwicklung könnte 2300 Windungen haben, die Sekundärwicklung 120 Windungen, so dass jeweils 10 Windungen an beiden Seiten auf ein Volt kommen. Die Stromstärke wird im gleichen Maß herauftransformiert wie die Spannung heruntertransformiert wird. Die Leistung ist daher primär wie sekundär mit 27,6 W gleich.
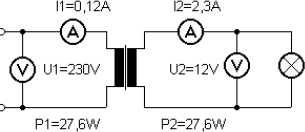
Abb. 3.3 Der Transformator
In der Realität besitzen Transformatoren jedoch einige abweichende Eigenschaften. Es treten ohmsche Verluste in beiden Wicklungen auf, die zu einem Spannungsabfall unter Belastung führen. Die nicht vollständige magnetische Kopplung zwischen den Wicklungen führt zu weiteren Spannungsverlusten, so dass die Sekundärwicklung insgesamt als eine Spannungsquelle mit einem gewissen Innenwiderstand erscheint. Dies berücksichtigt man, indem man das Wicklungsverhältnis für eine um etwa 10% größere Leerlaufspannung auslegt. Bei einem 12-V-Netztrafo aus dem obigen Beispiel bedeutet das eine Leerlauf-Effektivspannung von 13,2 V und eine Leerlauf-Spitzenspannung von ca. 18,7 V. Transformatoren sehr kleiner Leistung weisen noch größere Leerlaufspannungen und Spannungsverluste auf. Sehr große Transformatoren arbeiten dagegen mit sehr viel geringeren Verlusten.
Auch ohne eine Belastung fließt bereits ein Primärstrom durch den induktiven Widerstand der Primärspule. Bei einem idealen Transformator ist dies wie bei einer idealen Spule ein reiner Blindstrom, der zu keinen Verlusten führt. In der Realität kann man jedoch auch bei einem unbelasteten Transformator bereits eine Erwärmung feststellen, was auf Energieverluste hinweist.
Außer Spannungsabfällen treten bei Transformatoren auch gewisse nicht-lineare Effekte auf. Da man den Eisenkern nicht größer als unbedingt nötig auslegt, erreicht er in den Stromspitzen teilweise schon seine maximale Magnetisierung. Die dabei auftretenden Effekte führen zu einer Verzerrung der Kurvenformen und zu Energieverlusten im Kern. Die Verwendung höherer Frequenzen ermöglicht die Verwendung kleinerer Trafokerne bei zugleich geringeren Verlusten. Die relativ geringe Frequenz von 50 Hz führt zu großen und schweren Trafos. In Schaltnetzteilen verwendet man daher größere Frequenzen um etwa 50 kHz und erreicht damit insgesamt kleinere und preiswertere Transformatoren.
Wechselspannungen spielen auch als Signalspannungen eine wichtige Rolle. So sind z.B. Tonfrequenzsignale auf einer Telefonleitung oder an einem Lautsprecher ebenfalls Wechselspannungen, wobei aber meist mehrere Frequenzen im Bereich 20 Hz bis 20 kHz (Niederfrequenz) zusammen auftreten. Man kann typische Niederfrequenzsignale z.B. mit einem Oszilloskop untersuchen.
Bei der Übertragung von Tonsignalen über einen Transformator muss dieser für den gesamten Frequenzbereich ausgelegt sein, also z.B. für 20 Hz bis 20 kHz. Die Gefahr von Verzerrungen führt dazu, dass man NF-Übertrager nach Möglichkeit vermeidet. Im speziellen Fällen bieten sie jedoch Vorteile wie z.B. die Möglichkeit der Potentialtrennung zur Vermeidung von Brummschleifen. Bei größeren Anlagen mit vielen Lautsprechern verwendet man Verstärker in 100-V-Technik, wobei jeder Lautsprecher der Anlage einen eigenen Tonübertrager zur Anpassung erhält. Die früher in jedem Röhrenverstärker verwendeten Ausgangsübertrager können jedoch bei Transistorverstärkern völlig vermieden werden.
Kondensatoren sind Bauteile mit zwei Anschlussdrähten, deren Funktion sich vereinfacht als Ladungsspeicher beschreiben lässt. Schaltet man einen Kondensator im Gleichstromkreis in Reihe zu einem Verbraucher, dann ist der Stromkreis unterbrochen. Allenfalls beim ersten Einschalten fließt ein kurzer Stromstoß. Verwendet man dagegen Wechselspannung, dann fließt ein Strom, und der Kondensator verhält sich ähnlich wie ein Widerstand.
Abb. 3.4 Auf- und Entladen eines Kondensators
Der Kondensator besteht aus zwei Metallfolien, die gegeneinander isoliert sind. Bei Anschluss einer Spannung werden die Folien (Kondensatorplatten) aufgeladen, bis die Spannung gleich der Batteriespannung ist. Die Ladung bleibt gespeichert und kann beim Anschluss eines Widerstands in kurzer Zeit abfließen, wobei die Spannung abnimmt. Grundsätzlich fließt nur Strom, solange die Spannung sich ändert. Die Größe des Stroms hängt von der Plattengröße, von ihrem Abstand und vom verwendeten Isoliermaterial (Dielektrikum) ab. Man ordnet dem Kondensator als messbare Größe die Kapazität C in Farad (F) zu. Meist kommen Werte im Bereich Mikrofarad (µF, Millionstel Farad), Nanofarad (nF = 1/1000 µF) und Pikofarad (pF = 1/1000 nF) vor. Die Kapazität kann gemessen werden, wenn man den Spannungsanstieg ΔU bei einem Strom I in einer gewissen Zeit Δt bestimmt.
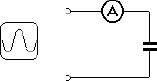
Abb. 3.5 Der Kondensator im Wechselstromkreis
Beim Anlegen einer Wechselspannung ändert sich die momentane Spannung zu jedem Zeitpunkt. Der Kondenstor wird also dauernd aufgeladen und wieder entladen. Es fließt ein Wechselstrom, der von der Spannung, der Frequenz und der Kapazität des Kondensators abhängt. Der Kondensator verhält sich ähnlich wie ein Widerstand und besitzt einen „kapazitiven Widerstand“ RC.
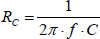
Für einen Kondensator mit C = 100 µF bestimmt man bei einer Frequenz von 50 Hz einen kapazitiven Widerstand von RC = 31,8 Ω.
Im Wechselstromkreis mit einem Kondensator ist zu beachten, dass es eine Phasenverschiebung zwischen Spannung und Strom gibt, d.h., der höchste Strom tritt nicht zum Zeitpunkt der höchsten Spannung auf, sondern früher. Aus diesem Grunde lassen sich auch nicht die Gesetze der Reihenschaltung einfach auf einen Kondensator und einen Widerstand anwenden. Trotzdem können Kondensatoren wie Vorwiderstände eingesetzt werden. Allerdings sind größere Kapazitäten meist nur bei Elektrolytkondensatoren erhältlich, die eine Polung aufweisen und nicht an Wechselspannung betrieben werden dürfen.
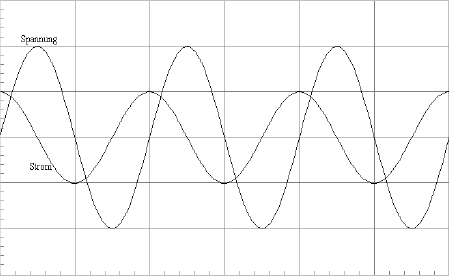
Abb. 3.6 Phasenverschiebung zwischen Spannung und Strom
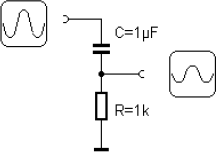
Abb. 3.7 Reihenschaltung aus Kondensator und Widerstand
Eine Reihenschaltung aus einem Widerstand und einem Kondensator bildet einen komplexen Gesamtwiderstand Z mit einem Betrag kleiner als der Summe aus R und RC. Außerdem tritt eine Phasenverschiebung zwischen Null und 90° auf. Allgemein gilt für den Betrag von Z:
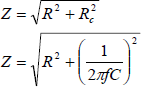
Für den Betrag des Stroms in Abhängigkeit von der Frequenz gilt für die Reihenschaltung aus R und C:
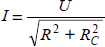
Der Strom I und damit auch der Spannungsabfall am Widerstand nimmt mit steigender Frequenz f zu. Deshalb spricht man hier von einem Hochpass. Ein wichtiger Punkt ist die sogenannte Grenzfrequenz fG..
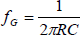
Im Beispiel mit R = 1 kΩ und C = 1 µF ergibt sich eine Grenzfrequenz von 159 Hz. Bei der Grenzfrequenz gilt R = RC. Die Impedanz der Gesamtschaltung ist Z = R*√2, im Beispiel also 1,41 kΩ. Damit ist die Spannung am realen Widerstand auf den Wert U*0,707 abgefallen.
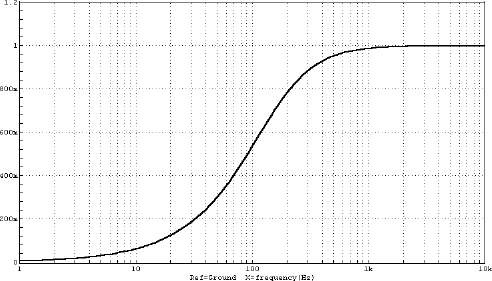
Abb. 3.8 Frequenzgang eines RC-Hochpass
Kondensatoren als Vorwiderstände setzt man in Lautsprecher-Frequenzweichen ein, um einen Hochpass zu realisieren. Ein Kondensator in Reihe zum Hochtonlautsprecher lässt also vornehmlich die hohen Frequenzen passieren. Mit C = 5 µF und einem Lautsprecherwiderstand von R = 8 Ω ergibt sich eine Grenzfrequenz von FG = 4 kHz.
Bisher wurden Kondensatoren nur im Wechselstromkreis mit sinusförmigen Spannungen betrachtet. Interessant ist jedoch auch das Verhalten des Kondensators bei Spannungssprüngen oder bei Rechteckspannungen. Ein echter Spannungssprung