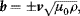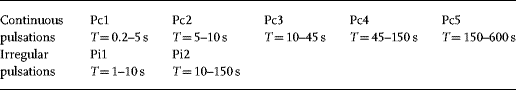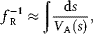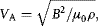Contents
Cover
Related Titles
Title Page
Copyright
Preface
Color Plates
Chapter 1: Introduction
1.1 Purpose of This Book
1.2 The Solar Wind
1.3 Fluctuations in the Solar Wind
1.4 Early Observations of Geomagnetic Variations
1.5 Properties of Geomagnetic Variations
Chapter 2: The Magnetosphere and Ionosphere
2.1 The Geomagnetic Field
2.2 Structure of Earth's Magnetosphere
2.3 Magnetospheric Current Systems
2.4 The Radiation Belts
2.5 The Inner Magnetosphere
2.6 Formation and Properties of the Ionosphere
2.7 Geomagnetic Disturbances
2.8 Space Weather Effects
Chapter 3: ULF Plasma Waves in the Magnetosphere
3.1 Basic Properties of a Plasma
3.2 Particle Motions
3.3 Low-Frequency Magnetized Plasma Waves
3.4 The Shear Alfvén Mode in a Dipole Magnetic Field
3.5 MHD Wave Mode Coupling in One Dimension
3.6 An Alternative Derivation of the Plasma Wave Equation, from Electromagnetism
Chapter 4: Sources of ULF Waves
4.1 Introduction
4.2 Exogenic Sources
4.3 Boundary Instabilities
4.4 Field Line Resonances
4.5 Cavity and Waveguide Modes
4.6 Spatially Localized Waves
4.7 Ion Cyclotron Waves
Chapter 5: Techniques for Detecting Field Line Resonances
5.1 Introduction
5.2 Variation in Spectral Power with Latitude
5.3 Variation of Phase with Latitude
5.4 Wave Polarization Properties
5.5 Spectral Power Difference and Division
5.6 Single Station H/D
5.7 Cross-Phase from Latitudinally Separated Sensors
5.8 Using ULF Wave Polarization Properties
5.9 Automated Detection Algorithms
Chapter 6: Ground-Based Remote Sensing of the Magnetosphere
6.1 Estimating Plasma Mass Density
6.2 Travel Time Method of Tamao
6.3 Determining Electron Density
6.4 Verification of Ground-Based Mass Density Measurements
6.5 Determining Ion Concentrations
6.6 Field-Aligned Plasma Density
6.7 Plasma Density at Low Latitudes
6.8 Plasma Density at High Latitudes
Chapter 7: Space Weather Applications
7.1 Magnetospheric Structure and Density
7.2 Plasmapause Dynamics
7.3 Density Notches, Plumes, and Related Features
7.4 Refilling of the Plasmasphere
7.5 Longitudinal Variation in Density
7.6 Solar Cycle Variations in Density
7.7 Determining the Open/Closed Field Line Boundary
7.8 Determining the Magnetospheric Topology at High Latitudes
7.9 Wave–Particle Interactions
7.10 Radial Motions of Flux Tubes
Chapter 8: ULF Waves in the Ionosphere
8.1 Introduction
8.2 Electrostatic and Inductive Ionospheres
8.3 ULF Wave Solution for a Thin Sheet Ionosphere
8.4 ULF Wave Solution for a Realistic Ionosphere
8.5 FLRs and the Ionosphere
8.6 Remote Sensing ULF Electric Fields in Space
8.7 Quarter-Wave Modes
8.8 Detection of ULF Waves in the Ionosphere
8.9 Consequences for Radio Astronomy
Chapter 9: Magnetoseismology at Other Planets and Stars
9.1 Magnetoseismology at Other Planets
9.2 Magnetoseismology of the Solar Corona
9.3 Introduction to Helioseismology and Asteroseismology
9.4 Field Line Resonances at Other Stars
Appendix A: Computer Codes
Appendix B: The Transverse MHD Wave Equation for General Magnetic Field Models
References
Index
All books published by Wiley-VCH are carefully produced. Nevertheless, authors, editors, and publisher do not warrant the information contained in these books, including this book, to be free of errors. Readers are advised to keep in mind that statements, data, illustrations, procedural details or other items may inadvertently be inaccurate.
Library of Congress Card No.: applied for
British Library Cataloguing-in-Publication Data
A catalogue record for this book is available from the British Library.
Bibliographic information published by the Deutsche Nationalbibliothek
The Deutsche Nationalbibliothek lists this publication in the Deutsche Nationalbibliografie; detailed bibliographic data are available on the Internet at <http://dnb.d-nb.de>.
© 2013 Wiley-VCH Verlag & Co. KGaA, Boschstr. 12, 69469 Weinheim, Germany
All rights reserved (including those of translation into other languages). No part of this book may be reproduced in any form – by photoprinting, microfilm, or any other means – nor transmitted or translated into a machine language without written permission from the publishers. Registered names, trademarks, etc. used in this book, even when not specifically marked as such, are not to be considered unprotected by law.
Print ISBN: 978-3-527-41027-9
ePDF ISBN: 978-3-527-65208-2
ePub ISBN: 978-3-527-65207-5
mobi ISBN: 978-3-527-65206-8
oBook ISBN: 978-3-527-65205-1
Typesetting Thomson Digital, Noida, India
Cover Design Matthew Waters
1
Introduction
1.1 Purpose of This Book
This book describes how measurements of naturally occurring variations of Earth's magnetic field can be used to provide information on the near-Earth space environment. This is a complex and highly dynamic region, the home of space weather that affects orbiting spacecraft and technological systems on the ground. The measurements come mostly from ground-based magnetometers but also from high-frequency radars, very low-frequency radio propagation circuits, and satellite platforms. Such remote sensing is possible because magnetic field lines originating in Earth extend through the atmosphere into space and respond to perturbations in the solar wind, which are transmitted earthward by periodic magnetic and electric field perturbations called plasma waves.
This area of research is called magnetoseismology. Its study and use for remote sensing require knowledge of and provide information on the solar wind, the interface between the solar wind and Earth's (geo)magnetic field, the near-Earth plasma environment and its variable particle populations, the ionized region of the atmosphere, and to some extent the subsurface structure of the ground.
The book does not assume familiarity with concepts in space physics and plasma physics. However, there is a strong emphasis on understanding of the core concepts and the consequent science applications. This is a new and exciting field, which greatly extends the utility of ground and in situ observations and mathematical descriptions of the observed phenomena.
1.2 The Solar Wind
Our planet Earth is immersed in the Sun's outer atmosphere. Particles streaming outward from the Sun exert pressure upon interplanetary matter, evident from observations of comet tails. As seen in Figure 1.1, comets may form two tails: a dust tail arising from the combined effects of radiation pressure on the low-mass dust particles and inertia of the heavier grains, and an ion tail due to the pressure exerted on gas in the comet's coma by the streaming solar particles and an embedded magnetic field. Biermann (1951) thus deduced that particles flow continuously outward from the Sun with velocities of order 103 km s−1. Parker (1959) called this stream the solar wind and showed that it arises from the supersonic expansion of the solar corona into space along magnetic lines of force originating in the Sun and due to the pressure gradient between the coronal gas (~10−3 Pa) and interplanetary space (~10−13 Pa). Further details appear in a number of reviews (e.g. Aschwanden, 2005; Goldstein et al., 2005; Hundhausen, 1995; Watermann et al., 2009). The solar wind energy flux reaching Earth's magnetosphere boundary is around 1012 W, imparting a force of order 4 × 107 N.
The solar wind carries with it an embedded magnetic field that extends from the Sun into interplanetary space. This is called the interplanetary magnetic field (IMF), and because of the high electrical conductivity of the solar wind plasma, the IMF is “frozen in” to the solar wind. This means that the magnetic flux through a volume of solar wind plasma remains constant, so the magnetic field is transported with the plasma and the field lines may be regarded as streamlines of the flow. Due to the conservation of angular momentum of the plasma, the field lines trace out Archimedean spiral patterns (called the Parker spiral) with distance from the Sun. This is an example of a rotating “garden hose” effect, so at Earth's orbit the IMF makes an azimuthal angle ϕ ≈ 45° with respect to the Sun–Earth line, given by
(1.1) 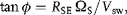
where RSE is the Sun–Earth distance, 1 AU (Astronomical Unit) = 1.50 × 109 m, ΩS is the angular rotation speed of the Sun ≈ 2.87 × 10−6 rad s−1, and Vsw is the solar wind speed.
The direction of the IMF is usually described in terms of vector components Bx, By, and Bz with respect to the Geocentric Solar Magnetospheric (GSM) coordinate system, in which the X-axis is directed from Earth to the Sun, the Z-axis points roughly northward such that Earth's magnetic dipole axis is in the X–Z plane, and the Y-axis completes the right-handed system. Since the polarity of solar magnetic fields is usually of one sign or the other over much of a hemisphere of the Sun, the IMF Bx component at Earth tends to be directed sunward or antisunward for extended periods of time. The boundary between these toward/away regions is referred to as the heliospheric current sheet, and in three dimensions the structure resembles a fluted ballerina skirt. This is illustrated in Figure 1.2. Under quiet conditions distinct crossings of these “sector boundaries” are observed during each solar rotation. The angle between the IMF and the Sun–Earth line is often called the cone angle, defined as
(1.2) 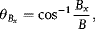
where B is the IMF magnitude. In reality, the cone angle fluctuates considerably, although it is often described as being small (≤40°) or large.
Properties of the solar wind are now well known (e.g. Hundhausen, 1995; Schwenn, 2001) and are monitored in real time by satellites upstream from Earth. The solar wind is highly variable over a range of timescales, but at Earth's orbit comprises a neutral, fully ionized plasma with typical ion composition of 95–96% protons, 4–5% He, and a minor proportion of heavy ions. Proton temperature is Tp ≈ 4–10 × 104 K and electron temperature Te ≈ 1.5 × 105 K. The average flow speed is VSW ≈ 350–400 km s−1, the proton density is typically in the range np = 3–10 cm−3, the resultant dynamic pressure (i.e., momentum flux,  ) is around 3 nPa, and the magnetic field strength is B ≈ 5 nT. The solar wind energy is dominated by the flow,
) is around 3 nPa, and the magnetic field strength is B ≈ 5 nT. The solar wind energy is dominated by the flow, 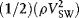 , which has energy density ~7 × 10−10 J m−3 at Earth. The speed VS at which pressure disturbances propagate in the solar wind is about 50 km s−1 at 1 AU, so the solar wind is supersonic, with Mach number Ms = VSW/VS.
, which has energy density ~7 × 10−10 J m−3 at Earth. The speed VS at which pressure disturbances propagate in the solar wind is about 50 km s−1 at 1 AU, so the solar wind is supersonic, with Mach number Ms = VSW/VS.
Various features of the solar corona determine the characteristics of the solar wind. Figure 1.3 shows normalized yearly solar wind speed distributions during solar minimum years derived from the NASA OMNIWeb database. A bimodal structure is evident, suggesting that there are two types of solar wind streams (McGregor et al., 2011; Schwenn, 2001). The high-speed, low-density solar wind streams originate from coronal holes, well-defined low-temperature regions from which coronal magnetic field lines are open to, and expand superradially into, interplanetary space. These are represented in Figure 1.2, and result in the formation of corotating interaction regions (CIRs) due to the tilt of the coronal magnetic field with respect to the Sun's rotation axis during the declining phase of the solar cycle (Gosling and Pizzo, 1999). Coronal holes are regarded as features of the quiet Sun, when they extend to lower latitudes on the solar surface, near the ecliptic plane. The helium abundance in such streams is higher and more constant than that under slow wind conditions, and the ionization state of heavier ions is lower, suggesting that the high-speed streams originate from lower and cooler altitudes in the corona.
The relatively slow component of the quiet solar wind typically has higher proton density, lower helium density, and higher ionization temperatures. It appears to originate from hotter magnetic loops that intermittently reconnect with open flux tubes at coronal hole boundaries.
During the active phase of the solar cycle, large transient events associated with active centers and closed loop-like magnetic structures are common. These include coronal mass ejections (CMEs), large eruptions of plasma and magnetic field into interplanetary space, causing interplanetary shocks and triggering geomagnetic storms at Earth when magnetic reconnection occurs between the CME and the geomagnetic field. The frequency of CME eruptions peaks near solar maximum, although a slow solar wind component, with high He+ concentration, is also present during this phase. Howard (2011) has provided a detailed review of current understanding of CMEs.
Multisatellite observations reveal the presence of complex features in the solar wind, including rotational and tangential discontinuities, magnetic clouds, flux ropes and holes, and isolated electrostatic structures indicative of the presence of double layers (Goldstein et al., 2005).
An extremely quiet solar wind condition occurred during May 11–12, 2009, when the solar wind density dropped to ≤0.2 cm−3 and the velocity to ~300 km s−1 for an extended period. This event was associated with highly nonradial solar wind flows and unipolar IMF and has been traced to a small coronal hole lying adjacent to a large active region on the solar disk (Janardhan et al., 2008). In contrast, a series of violent solar flares and CMEs during late October to early November 2003 triggered major geomagnetic storms at Earth resulting in extreme space weather events with significant impacts on Earth-orbiting spacecraft, the ionosphere and atmosphere, and terrestrial systems (Gopalswamy et al., 2005). During this time, solar wind gusts exceeding 2000 km s−1 were accompanied by increases in the >10 MeV proton flux at geostationary orbit of over five orders of magnitude relative to nominal quiet conditions.
1.3 Fluctuations in the Solar Wind
The region of interplanetary space dominated by the solar wind is the heliosphere. At some large distance from the Sun, the solar wind speed (which depends on density) becomes subsonic, with large changes in plasma flow direction and magnetic field orientation. This is the termination shock. Beyond this is a shock region and the heliopause, where solar wind particles encounter and are stopped by particles of the interstellar medium. The Voyager 1 and Voyager 2 spacecraft, launched 2 weeks apart in 1977, crossed the termination shock in December 2004 and August 2007, respectively, at about 94.0 AU in the northern hemisphere and 83.6 AU in the southern hemisphere.
Plasma waves are a characteristic feature of shocks, where they dissipate energy and drive particle motions, and have been observed in bow shocks upstream of the magnetized planets and also at the solar wind termination shock (e.g. Gurnett and Kurth, 2008). Since the termination shock may move due to variations in the solar wind dynamic pressure or waves on the shock front, Voyager 2 has been seen to cross the shock multiple times (Li, Wang, and Richardson, 2008). By December 2010, the solar wind recorded by Voyager 1 at 116 AU had zero radial component and was purely parallel to the heliosphere surface.
The solar wind is full of fluctuations, although whether this is due to turbulence or waves is not always evident from single point measurements (Goldstein et al., 2005; Tu and Marsch, 1995). A correlation often exists between magnetic field and velocity fluctuations. If the perturbed magnetic field b = δB is related to the velocity perturbation v = δV and number density ρ in the form
(1.3) 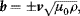
then the perturbation is said to be Alfvénic and may be related to the propagation of transverse Alfvén plasma waves. These waves are described in detail in Chapter 3. High-speed solar wind streams contain a complex spectrum of wave-like oscillations in velocity, density, and magnetic field strength, with periods ranging from seconds to days (Gurnett, 2001), while large-amplitude, nonsinusoidal Alfvén waves that probably originate in coronal holes and propagate outward from the Sun dominate the microscale structure of the solar wind (Belcher and Davis, 1971).
Power spectra from near-Earth orbit of solar wind magnetic field fluctuations in the millihertz frequency range often follow a power law similar to that for uncorrelated turbulence, of the form f−5/3. Monthly averaged spectra of solar wind speed and density from upstream satellites exhibit no statistically significant peaks, as shown in Figure 1.4, although magnetic fluctuations may occur specifically near the local proton gyrofrequency (Jian et al., 2010; Tsurutani et al., 1994). Plasma waves play a fundamental role in determining the properties of the solar wind, and can also be used as a diagnostic of energetic processes. Such plasma waves are an important focus of this book.
Oscillations exist within the Sun in the form of pressure and gravity waves. The latter are trapped in the deep interior of the Sun below the convection zone, while the former can propagate throughout the Sun's interior. Acoustic waves can thus propagate around the Sun and arrive in phase at the original point to form global standing modes, called normal modes, producing surface oscillations as the wave energy couples with the boundary of the cavity. This boundary is usually the photosphere where the density decreases rapidly.
Study of these surface oscillations provides insights into the internal structure and dynamics of the Sun (Christensen-Dalsgaard, 2002). This area of science is called helioseismology, while the study of the internal structure of other stars using similar techniques is called asteroseismology. Chapter 9 provides a brief introduction to these interesting topics. The period of the solar normal mode oscillations is about 5 min (3.33 mHz), although long-duration ground-based observations reveal a multitude of Doppler shift frequency peaks between about 2.5 and 4.5 mHz in power spectra of the Sun's full disk (Claverie et al., 1979; Grec, Fossat, and Pomerantz, 1980). The precise frequencies vary with solar cycle. Plasma waves are believed to play an important role in heating the corona, and 5 min waves have been observed in the photosphere. Near Earth, there are many reports of geomagnetic field oscillations with discrete frequencies in the range 1.4–4.2 mHz (e.g. Mathie et al., 1999a; Viall, Kepko, and Spence, 2009). It has been suggested that discrete frequencies similar to those observed at Earth in the millihertz range are present in the solar wind density (Walker, 2002) and may originate from the corona (Viall, Spence, and Kasper, 2009). The sources of millihertz frequency plasma waves are discussed in more detail in Chapter 4.
1.4 Early Observations of Geomagnetic Variations
Oscillatory variations of suspended magnetic needles were noted by several workers during the mid-nineteenth century (Schröder and Wiederkehr, 2000), including Johann von Lamont in 1841 and Balfour Stewart in 1859. The development of magnetometers, in London in 1857, using a light beam to record small variations on photosensitive waxed sheets permitted the continuous registration of geomagnetic (micro)pulsations at a number of observatories (Stewart, 1859). This allowed Stewart (1861) to note that great auroral displays seen on August 28 and September 2, 1859 at latitudes as low as Cuba and Australia were accompanied by rapid pulsatory magnetic variations with periods ranging from 0.5 min (the smallest observable interval) to 4–5 min, similar to “the nature of its action on telegraphic wires” in addition to longer variations with periods of 40–50 min and about 6 h. Remarkably, Stewart considered that an intense magnetic disturbance commencing at 05 LT on September 2, 1859 was related to solar flare eruptions, observed for the first time at 1115 LT on the previous day by Carrington. He also noted that at the instant of the flare observation, there was an abrupt magnetic disturbance lasting about 7 min. This phenomenon is now called a solar flare effect (SFE).
We now know that solar flares and CMEs trigger magnetic storms, resulting in disturbances in the geomagnetic field with periods from fractions of a second to many hours, intense auroral activity at high latitudes, and a host of other effects including space weather impacts on satellites, radio networks, and terrestrial systems. Ground-based measurements of geomagnetic variations may be used to remote sense the regions where these effects are produced. The remote sensing techniques are described in Chapter 6 and examples of applications are given in Chapter 7.
In 1896, Eschenhagen recorded geomagnetic perturbations using rapid run magnetographs with tiny suspended magnets, finding small-amplitude oscillations with a period of 12 s. Such phenomena were called geomagnetic pulsations by van Bemmelen in 1899. Using measurements at 15 observatories worldwide, Eschenhagen (1897) concluded that these fluctuations can originate in the uppermost levels of the atmosphere “unless they are first caused by special activity on the Sun itself.”
Since these first observations, many thousands of papers have appeared in the refereed literature on the properties and origin of what are now called geomagnetic pulsations. The region of near-Earth space in which they are found is termed the magnetosphere, since it is enclosed and dominated by the geomagnetic field. The development of knowledge on geomagnetic pulsations may be traced through detailed reviews (Allan and Poulter, 1992; Chapman and Bartels, 1940; Kato and Watanabe, 1957; Menk, 2011; Orr, 1973; Saito, 1969).
Advances in instrumentation and data analysis techniques have stimulated this growth in understanding. These include the development of induction coil and fluxgate sensors and digital data loggers (Serson, 1973), the use of spectrum analysis techniques to display whole day frequency–time spectra (Duncan, 1961) and cross-phase spectra between closely spaced ground magnetometers (Waters, Menk, and Fraser, 1991), and the detection with high-frequency radars of perturbations in the ionosphere accompanying geomagnetic variations (Harang, 1939). These techniques are described in Chapter 5.
1.5 Properties of Geomagnetic Variations
Intense work during the International Geophysical Year, (1957–1958) established that small, periodic oscillations of the geomagnetic field occur virtually at all times and across the globe, although their amplitudes peak at high latitudes. The pulsations are generally of two forms in ground-based magnetometer records. Regular, sinusoidal oscillations with periods between about 0.1 and 1000 s occur mostly during local daytime, and are called continuous pulsations, Pc. They last from minutes to hours, often exhibiting a characteristic modulated waveform similar to the beating pattern produced by signals with closely spaced frequencies. The amplitude of these pulsations increases with increasing period and is of order 1 nT at 30 s (33 mHz). For comparison, the main background geomagnetic field on the ground has intensity of ~5 × 104 nT. The amplitude of Pc signals also exhibits a diurnal variation, typically peaking near noon, varies with solar wind conditions, and is strongly dependent on latitude.
Figure 1.5a shows an early measurement of the relation between amplitude and period of Pc pulsation activity at a midlatitude station, while Figure 1.5b represents the variation with latitude of Pc occurrence frequency at solar maximum.
At local nighttime, pulsations have the appearance of impulsive damped trains of oscillations, called Pi, and are often associated with auroral activity and other geomagnetic disturbances.
To lend order to descriptions of magnetic pulsations, Jacobs et al. (1964) proposed a classification system based on the frequency bands in which oscillations tend to be observed. This is summarized in Table 1.1.
Table 1.1 Classification system for geomagnetic pulsations.
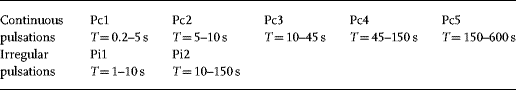
Although this classification did not attempt to describe the essential physics of the phenomena, it is still widely used today. Descriptions of the appearance of these signals in frequency–time spectra have been provided by several workers (e.g. Fukunishi et al., 1981; Menk, 1988; Saito, 1969). As seen in Figure 1.6, daytime pulsation activity is often present in one or more well-defined spectral bands lasting up to several hours. This suggests the pulsations are generated by mechanisms that select specific frequencies for a given location.
A landmark in the understanding of geomagnetic pulsations was the realization by Hannes Alfvén in 1942 that the motion of a conducting fluid in a magnetic field gives rise to electric currents, which in turn produce mechanical forces, resulting in the formation of hydrodynamic waves propagating through space at what is today called the Alfvén speed. These ideas were developed in detail by Alfvén (1948) with the formulation of the theory of hydromagnetic waves (now called Alfvén waves) and the field of magnetohydrodynamics (MHD). Hannes Alfvén was awarded the 1970 Nobel Prize in Physics for “fundamental work and discoveries in magneto-hydrodynamics with fruitful applications in different parts of plasma physics.” The theory and properties of plasma waves in the magnetosphere are described in Chapter 3.
It is now known that geomagnetic pulsations are the signature of ultralow frequency (ULF) (frequency in the range 1 mHz–10 Hz) waves that propagate through Earth's magnetosphere. There is growing evidence that Pc pulsations are connected with ULF waves, which enter the magnetosphere from the upstream solar wind or are generated at the magnetopause boundary when it undergoes rapid deformation under the action of the solar wind. These waves may have dimensions comparable to the size of the entire magnetosphere, and may therefore establish oscillations along geomagnetic field lines stretching from Earth into space. Some Pc pulsations with low spatial coherence lengths are associated with waves generated locally within the magnetosphere, and gain energy from interactions with charged particles orbiting Earth in the radiation belts. Pi pulsations are manifestations of irregular ULF waves associated with the transient magnetic fields and precipitating energetic particles responsible for auroras.
ULF waves carry energy throughout the magnetosphere, but can also be used to monitor processes in space. Obayashi and Jacobs (1958) suggested that long-period magnetic pulsations are due to standing Alfvén waves on geomagnetic field lines, called field line resonances (FLRs). The concept of standing oscillations, assisted by MHD theory, is often described in terms of two limiting types of standing oscillations, toroidal and poloidal modes, as represented in Figure 1.7. These relate respectively to azimuthal and radial motions of field lines in space. The oscillation frequency of the fundamental mode, fR, depends on the field line length and the Alfvén speed VA along the resonant field line:
(1.4) 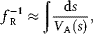
where
(1.5) 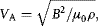
ρ = nimi is the plasma mass density, μ0 is the permeability of space, and the integration is carried out between conjugate ionospheres. Since field lines originating at different latitudes on the ground have different lengths and hence map out to different radial distances in space, measurement of the FLR frequency as a function of latitude provides an estimate of magnetospheric plasma mass density distribution provided the magnetic field strength is known. This is the basis for remote sensing near-Earth space described in this book.
























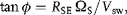
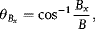

 ) is around 3 nPa, and the magnetic field strength is
) is around 3 nPa, and the magnetic field strength is 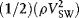 , which has energy density ~7 × 10−10 J m−3 at Earth. The speed
, which has energy density ~7 × 10−10 J m−3 at Earth. The speed