Albert Einstein, Mein Weltbild, Frankfurt/Main, Berlin 1993, S. 117.

Überraschenderweise haben die Physiker auch heute noch keine richtige Antwort für dieses Rätsel. Im Laufe der Jahrzehnte haben wir uns einfach an die Vorstellung gewöhnt, dass sich Licht in einem Vakuum ausbreitet, auch wenn dort nichts ist, was schwingen kann.

Heinz Pagels, Die Zeit vor der Zeit. Das Universum bis zum Urknall, Berlin 1987, S. 346.

Peter Freund, Gespräch mit dem Autor, 1990.

Die Theorie höherer Dimensionen hat also offenkundig nicht bloß akademischen Wert, denn die einfachste Folge der Einstein’schen Theorie ist die Atombombe, die das Schicksal der Menschheit verändert hat. Insofern war die Einführung höherer Dimensionen eine der entscheidendsten Entdeckungen in der gesamten Menschheitsgeschichte.

Zitiert in: Abraham Pais, Raffiniert ist der Herrgott, Braunschweig 1986, S. 237.

Freund schmunzelt, wenn man ihn fragt, wann wir in der Lage sein werden, diese höheren Dimensionen zu sehen. Wir können sie nicht erblicken, weil sie sich zu einer winzigen Kugel «aufgewickelt» haben, die für das Auge nicht erkennbar ist. Nach der Kaluza-Klein-Theorie entsprechen die Ausmaße dieser aufgewickelten Dimensionen der Planck’schen Länge*, die einhundert Milliarden Milliarden Mal kleiner als ein Proton ist, zu klein, um selbst in unseren größten Atomzertrümmerern erscheinen zu können. Hochenergiephysiker hatten gehofft, der elf Milliarden Dollar teure supraleitende Supercollider (SSC), dessen Bewilligung im Oktober 1993 vom amerikanischen Kongreß gestrichen wurde, würde einige indirekte Hinweise auf den Hyperraum liefern.

* Diesem unglaublich kleinen Abstand werden wir im Verlaufe dieses Buches fortwährend wiederbegegnen. Er ist das grundlegende Längenmaß, das jede Quantentheorie der Gravitation charakterisiert. Das hat einen ganz einfachen Grund. In jeder Gravitationstheorie wird die Stärke der Gravitationskraft durch die Newton’sche Konstante gemessen. Nun verwenden Physiker aber ein vereinfachtes Einheitssystem, in dem die Lichtgeschwindigkeit c gleich eins gesetzt wird. Das heißt, eine Sekunde entspricht 300000 Kilometern. Auch die Planck’sche Konstante geteilt durch 2p wird gleich eins gesetzt, was eine numerische Beziehung zwischen Sekunden und der Energie-Einheit Erg herstellt. In diesen seltsamen, aber bequemen Einheiten lässt sich alles, auch die Newton’sche Konstante, auf Zentimeter verringern. Wenn wir die Länge berechnen, die mit der Newton’schen Konstante verknüpft ist, gelangen wir exakt zur Planck’schen Länge oder 10^–33 Zentimeter oder 10¹⁹ Milliarden Elektronenvolt. Folglich werden alle Quantengravitationseffekte mit Hilfe dieses winzigen Abstands gemessen. Vor allem aber entspricht auch die Größe dieser unsichtbaren höheren Dimensionen der Planck’schen Länge.

Linda Dalrymple Henderson, The Fourth Dimension and Non-Euclidean Geometry in Modern Art, Princeton 1983, S. XIX.

E.T. Bell, Die großen Mathematiker, Düsseldorf, Econ-Verlag, 1967, S. 459.

A.a.O., S. 461. Höchstwahrscheinlich hat dieser Vorfall für Riemanns frühes Interesse an der Zahlentheorie gesorgt. Jahre später sollte er eine berühmte Spekulation über eine bestimmte Formel anstellen, die mit der Zetafunktion in der Zahlentheorie zu tun hatte. Nachdem sich die größten Mathematiker der Welt hundertzwanzig Jahre mit der «Riemann’schen Vermutung» herumgeschlagen haben, warten wir noch immer auf einen Beweis. Selbst modernste Computer können uns nicht weiterhelfen, und die Riemann’sche Vermutung ist inzwischen in die Geschichte eingegangen als einer der berühmtesten unbewiesenen Lehrsätze in der Zahlentheorie, vielleicht in der gesamten Mathematik. Dazu Bell: «Wer sie beweist oder widerlegt, wird höchsten Ruhm ernten.»

John Wallis, Der Barycentrische Calcul, Leipzig 1827, S. 184.

Obwohl Riemann heute als die treibende schöpferische Kraft gilt, der es endlich gelang, die Grenzen der euklidischen Geometrie aufzuheben, hätte von Rechts wegen Riemanns alternder Mentor Gauß der Mann sein müssen, der die Geometrie der höheren Dimensionen entdeckte.

Schon 1817, fast zehn Jahre vor Riemanns Geburt, brachte Gauß in privatem Gespräch seine tiefe Unzufriedenheit mit der euklidischen Geometrie zum Ausdruck. In einem prophetischen Brief an seinen Freund, den Astronomen Heinrich Olbers, erklärte er unmissverständlich, dass die euklidische Geometrie mathematisch unvollständig sei.

1869 hielt der Mathematiker James J. Sylvester fest, dass Gauß die Möglichkeit höherdimensionaler Räume ernsthaft in Betracht gezogen habe. Danach stellte sich Gauß die Eigenschaften von Wesen vor, die er «Bücherwürmer» nannte und die vollständig auf zweidimensionalen Papierbögen leben können. Daraufhin verallgemeinerte er dieses Konzept so, dass es auch Wesen einbezog, die «fähig sind, Räume mit vier oder einer größeren Anzahl von Dimensionen wahrzunehmen» (zitiert in: Linda Dalrymple Henderson, The Fourth Dimension and Non-Euclidean Geometry in Modern Art, a.a.O., S. 19).

Doch wenn Gauß die Theorie höherer Dimensionen schon vierzig Jahre früher formulieren konnte, was hinderte ihn dann, diese historische Chance wahrzunehmen und die Fesseln der dreidimensionalen euklidischen Geometrie zu sprengen? Historiker haben bei Gauß eine konservative Tendenz in seiner Arbeit, seinen politischen Ansichten und seinem persönlichen Leben beobachtet. Tatsächlich hat er Deutschland nicht ein einziges Mal verlassen und fast sein ganzes Leben in einer einzigen Stadt verbracht. Das hat sich auch auf seinen Beruf ausgewirkt.

In einem Brief aus dem Jahr 1829 gestand Gauß seinem Freund Friedrich Bessel, er werde seine Arbeit über nichteuklidische Geometrie aus Angst vor der Kontroverse, die sie unter den «Böotiern» auslösen werde, nie veröffentlichen. Dazu der Mathematiker Morris Kline: «[Gauß] meinte in einem Brief an Bessel vom 27. Januar 1829, er werde seine Ergebnisse zu diesem Thema niemals veröffentlichen, weil er fürchte, sich lächerlich zu machen, oder wie er sagte, aus Angst vor dem Lärm der Böotier, eine symbolische Anspielung auf einen stumpfsinnigen griechischen Stamm» (Mathematics and the Physical World, New York 1959, S. 449). Gauß fühlte sich so eingeschüchtert von der alten Garde, den engstirnigen «Böotiern», für die die drei Dimensionen einen geradezu geheiligten Charakter hatten, dass er einige seiner besten Arbeiten geheim hielt.

1869 meinte Sylvester in einem Gespräch mit dem Gauß-Biographen Sartorius von Waltershausen: «Dieser große Mann sagte häufig, er habe etliche Fragen beiseite gelassen, die er analytisch behandelt habe, und hoffe, in einer künftigen Existenz analytische Methoden auf sie anzuwenden, wenn er seine Vorstellungen vom Raum verbessert und erweitert hätte; denn wie wir uns Wesen denken könnten (etwa unendlich schlanke Bücherwürmer auf einem unendlich dünnen Bogen Papier), die sich einen Begriff nur von einem Raum mit zwei Dimensionen machen könnten, so ließen sich auch Wesen denken, die in der Lage seien, einen Raum von vier oder mehr Dimensionen zu erfassen» (zitiert in: Henderson, Fourth Dimension and Non-Euclidean Geometry in Modern Art, S. 19).

Gauß schrieb an Olbers: «Ich bin mehr und mehr davon überzeugt, dass sich die (physikalische) Notwendigkeit unserer (euklidischen) Geometrie nicht beweisen lässt, zumindest nicht von menschlicher Vernunft für menschliche Vernunft. Vielleicht werden wir in einem anderen Leben in der Lage sein, Einsicht in das Wesen des Raumes zu gewinnen, etwas, was uns jetzt verschlossen ist. Bis dahin dürfen wir die Geometrie nicht der gleichen Klasse zurechnen wie die Arithmetik, die ein reines Apriori ist, sondern der gleichen Klasse wie die Mechanik» (zitiert in: Mathematical Thought from Ancient to Modern Times, New York 1972, S. 872).

So misstrauisch stand Gauß der euklidischen Geometrie gegenüber, dass er sie sogar in einem einfallsreichen Experiment überprüfte. Seine Assistenten und er erklommen drei Berggipfel: Rocken, Hohehagen und Inselsberg. Von jedem Gipfel waren die beiden anderen deutlich sichtbar. Zwischen den drei Bergen zog Gauß ein Dreieck und konnte so die Innenwinkel experimentell messen. Wenn die euklidische Geometrie richtig ist, hätte die Winkelsumme 180 Grad betragen müssen. Zu seiner Enttäuschung kam Gauß tatsächlich auf 180 Grad (plus/minus 15 Minuten). Seine Meßinstrumente waren zu ungenau, um Euklid zu widerlegen. (Heute wissen wir, dass er dieses Experiment zwischen drei verschiedenen Sternensystemen hätte durchführen müssen, um eine greifbare Abweichung von Euklids Resultat zu erhalten).

Es sei auch erwähnt, dass die Mathematiker Nikolaus I. Lobatschewski und János Bolyai unabhängig voneinander die nichteuklidische Mathematik auf gekrümmten Flächen entdeckten. Allerdings blieb ihr System auf die übliche niedrige Dimensionalität beschränkt.

Zitiert in: Bell, Die großen Mathematiker, S. 469.

Der englische Mathematiker William Clifford, der 1873 Riemanns berühmten Vortrag für die Zeitschrift Nature übersetzte, führte viele von Riemanns bahnbrechenden Ideen fort und ist vielleicht als Erster näher auf den Riemann’schen Gedanken eingegangen, dass die Raumkrümmung der Grund für die Kraft der Elektrizität und des Magnetismus sein könnte, womit er Riemanns Arbeit eine feste Form gab. Clifford äußerte die Vermutung, die beiden geheimnisvollen Entdeckungen in der Mathematik (der höherdimensionale Raum) und in der Physik (Elektrizität und Magnetismus) seien in Wirklichkeit die gleiche Sache, das heißt, die elektrische und magnetische Kraft werde durch die Krümmung des höherdimensionalen Raumes hervorgerufen.

Damit wurde zum ersten Mal die Überlegung angestellt, eine «Kraft» sei nichts anderes als die Krümmung des Raumes selbst, ein Gedanke, der Einsteins Arbeit um fünfzig Jahre voraus war. Mit der Vorstellung, Elektromagnetismus werde durch Schwingungen in der vierten Dimension verursacht, nahm Clifford auch die Arbeit von Theodor Kaluza vorweg, der dieses Phänomen ebenfalls durch eine höhere Dimension zu erklären versuchte. Damit antizipierten Clifford und Riemann die bahnbrechenden Entdeckungen des 20. Jahrhunderts, die zeigen, dass die Bedeutung des höherdimensionalen Raums in seiner Fähigkeit liegt, eine einfache und elegante Beschreibung von Kräften zu liefern. Zum ersten Mal offenbarten die höheren Dimensionen damit ihren wahren physikalischen Charakter: Eine Theorie über den Raum vermittelt uns in Wirklichkeit ein einheitliches Bild der Kräfte.

Diese prophetischen Ausblicke hat der Mathematiker James Sylvester 1869 festgehalten, als er schrieb: «Mr. W.K. Clifford hat einige bemerkenswerte Spekulationen über die Möglichkeit angestellt, aus bestimmten unerklärten Erscheinungen des Lichtes und des Magnetismus zu schließen, dass sich unser Raum von drei Dimensionen im Übergang zu einem Raum von vier Dimensionen befinde … eine Verformung, die dem Knüllen eines Papierbogens entspricht» (zitiert in: Henderson, Fourth Dimension and Non-Euclidean Geometry in Modern Art, S. 19).

In einem Artikel mit dem hochinteressanten Titel On the Space-Theory of Matter aus dem Jahr 1870 heißt es explizit: «Diese Veränderung der Raumkrümmung ist das, was bei jener Erscheinung tatsächlich geschieht, die wir, ob wägbar oder ätherisch, Bewegung von Materie nennen» (William Clifford, ‹On the Space-Theory of Matter›, Proceedings of the Cambridge Philosophical Society, 2, 1876, S. 157–158).

Genauer: In n Dimensionen ist der Riemann’sche Maßtensor g_μν eine n × n-Matrix, die den Abstand zwischen zwei Punkten bestimmt, dergestalt, dass der infinitesimale Abstand zwischen zwei Punkten gegeben wird durch ds² = Σdx^μ g_μν dx^ν. In den Grenzen des flachen Raums wird der Riemann’sche Maßtensor diagonal, das heißt g_μν = δ_μν, und damit reduziert sich das Gleichungssystem auf den pythagoreischen Lehrsatz in n Dimensionen. Die Abweichung des Maßtensors von δ_μν misst, grob gesagt, die Abweichung des Raums vom flachen Raum. Aus dem Maßtensor können wir den Riemann’schen Krümmungstensor bilden, ausgedrückt durch R^β_μνa..

Die Raumkrümmung lässt sich an jedem gegebenen Punkt dadurch messen, dass wir an diesem Punkt einen Kreis ziehen und die Fläche im Inneren des Kreises messen. Im flachen zweidimensionalen Raum entspricht die Fläche im Inneren des Kreises πr². Doch wenn die Krümmung positiv ist, wie bei einer Kugel, ist die Fläche kleiner als πr². Ist die Krümmung negativ, wie bei einem Sattel oder einer Trompete, ist die Fläche größer als πr². Streng genommen ist nach dieser Regel die Krümmung eines zerknüllten Papierbogens null, denn die Flächen der Kreise, die man auf einen solchen Bogen gezeichnet hat, sind immer noch gleich πr². In Riemanns Beispiel für eine Kraft, die durch das Knüllen eines Papierbogens hervorgerufen wird, setzen wir stillschweigend voraus, dass das Papier nicht nur gefaltet, sondern auch verformt und gestreckt wird, sodass die Krümmung nicht gleich null ist.

Zitiert in: Bell, Die großen Mathematiker.

A.a.O.

Ebenda.

1917 schrieb der Physiker Paul Ehrenfest, ein Freund Einsteins, einen Artikel mit dem Titel In What Way Does It Become Manifest in the Fundamental Laws of Physics that Space has Three Dimensions? Dort fragte Ehrenfest sich, ob Sterne und Planeten in höheren Dimensionen möglich sind. Beispielsweise wird das Licht einer Kerze dunkler, wenn wir uns von ihr fortbewegen. Ebenso nimmt die Anziehungskraft eines Sterns mit der Entfernung ab. Laut Newton wird die Gravitation gemäß einem umgekehrten quadratischen Gesetz schwächer. Wenn wir den Abstand zwischen einer Kerze oder einem Stern verdoppeln, wird das Licht oder die Anziehungskraft viermal so schwach. Verdreifachen wir den Abstand, so beträgt die Schwächung das Neunfache.

Wenn der Raum vierdimensional wäre, würden sich Kerzenlicht und Gravitation noch sehr viel rascher abschwächen, nämlich gemäß einem umgekehrt kubischen Gesetz, das heißt, bei Verdoppelung des Abstandes von einer Kerze oder einem Stern würden Licht beziehungsweise Gravitation um einen Faktor von acht abnehmen.

Können Sonnensysteme in einer solchen vierdimensionalen Welt existieren? Im Prinzip ja, aber die Umlaufbahnen der Planeten wären nicht stabil. Bei der geringsten Schwingung brächen die Planetenbahnen zusammen. Deshalb würden im Laufe der Zeit alle Planeten aus ihrer ursprünglichen Bahn geraten und in die Sonne stürzen. Auch die Sonne könnte in höheren Dimensionen nicht existieren. Die Gravitationskraft ist bestrebt, die Sonne in sich zusammenstürzen zu lassen. Sie wird aufgewogen durch die Fusionskraft, die bestrebt ist, die Sonne explodieren zu lassen. Folglich befindet sich die Sonne in einem empfindlichen Gleichgewicht zwischen den Kernkräften, die auf ihre Sprengung hinwirken, und den Gravitationskräften, die sie zu einem Punkt zusammenziehen möchten. In einem höherdimensionalen Universum wäre dieses empfindliche Gleichgewicht gestört, sodass die Sterne spontan kollabieren würden.

Henderson, Fourth Dimension and Non-Euclidean Geometry in Modern Art, S. 22.

Zum Spiritismus wurde Zöllner 1875 bekehrt, als er das Labor von Crookes besuchte, dem Entdecker des Elements Thalium, dem Erfinder der Kathodenstrahlröhre und Herausgeber des seriösen Quarterly Journal of Science. Crookes’ Kathodenstrahlröhre revolutionierte die Wissenschaft; wer heute fernsieht, sich mit einem Videospiel vergnügt oder geröntgt wird, ist dazu nur dank der technischen Entwicklung infolge Crookes’ berühmter Erfindung fähig.

Nun war Crookes keineswegs ein Spinner, sondern ein geachtetes Mitglied der wissenschaftlichen Gemeinschaft Englands. 1897 wurde er geadelt, und 1910 erhielt er den Order of Merit. Sein intensives Interesse am Spiritismus wurde 1867 durch den tragischen Tod seines Bruders Philipp an Gelbfieber ausgelöst. Er wurde ein prominentes Mitglied (und später Präsident) der Society for Psychical Research, der Ende des 19. Jahrhunderts eine erstaunliche Anzahl bedeutender Wissenschaftler angehörten.

Zitiert in: Rudy Rucker, The Fourth Dimension, Boston 1984, S. 54.

Um eine Vorstellung davon zu bekommen, wie sich Knoten in mehr als drei Dimensionen lösen lassen, stellen wir uns zwei verschlungene Ringe vor. Nun fertigen wir einen zweidimensionalen Querschnitt dieser Anordnung an, sodass ein Ring auf der Ebene liegt, während der andere zu einem Punkt wird (weil er senkrecht zur Ebene steht). Wir haben jetzt einen Punkt in einem Kreis. In höheren Dimensionen ergibt sich die Möglichkeit, diesen Punkt ganz aus dem Kreis herauszubewegen, ohne einen der Ringe zu zerteilen. Damit haben wir, wie gewünscht, beide Ringe völlig voneinander getrennt. Das heißt, in mehr als drei Dimensionen lassen sich Knoten immer lösen, weil «genügend» Platz vorhanden ist. Es ist aber festzuhalten, dass der Punkt sich im dreidimensionalen Raum nicht aus dem Ring entfernen lässt; deshalb bleiben Knoten nur in der dritten Dimension verknotet.

Dass der Roman (Leipzig 1929) aus der Feder eines Geistlichen stammt, ist nicht überraschend, denn die Theologen der Kirche von England gehörten zu den ersten, die sich in den Streit um den Sensationsprozess einmischten. Seit Jahrhunderten drückte sich der Klerus geschickt vor Fragen wie: Wo befinden sich Himmel und Hölle? und: Wo leben Engel? Nun hatte er endlich einen geeigneten Ort für solche Himmelsexistenzen gefunden: die vierte Dimension. Der christliche Spiritualist A.T. Schofield hatte 1888 in seinem Buch Another World lang und breit die Auffassung dargelegt, dass Geister in der vierten Dimension leben.* Doch den Vogel schoss 1893 der Theologe Arthur Willink ab, als er The World of the Unseen schrieb und behauptete, es sei Gottes nicht würdig, in der niederen vierten Dimension zu leben. Nach Willink wird Gottes Herrlichkeit allein der unendlich-dimensionale Raum gerecht.**

* A.T. Schofield schrieb: «Wir gelangen deshalb erstens zu dem Schluss, dass eine höhere Welt als die unsere nicht nur denkbar, sondern wahrscheinlich ist; zweitens, dass eine solche Welt vier Dimensionen haben dürfte; und drittens, dass die spirituelle Welt in ihren geheimnisvollen Gesetzen weitgehend mit dem übereinstimmt … was analog die Gesetze, sprachlichen Gegebenheiten und Ansprüche einer vierten Dimension wären» (zitiert in: Rucker, The Fourth Dimension, S. 56).

** Arthur Willink schrieb: «Wenn wir erst einmal die Existenz eines Raums von vier Dimensionen anerkannt haben, dann ist ohne Schwierigkeiten auch ein Raum von fünf Dimensionen vorstellbar und so fort bis hin zu einem Raum mit einer unendlichen Zahl von Dimensionen» (zitiert in: a.a.O., S. 200).

Oscar Wilde, Das Gespenst von Canterville, Werke in zwei Bänden, Bd. 1, München 1970, S. 353.

Die Vorstellung, dass man die Zeit als eine neue Art vierter Dimension ansehen kann – im Unterschied zu der des Raumes – stammt nicht von Wells. Schon 1754 hat Jean d’Alembert in dem Artikel Dimension die Zeit als vierte Dimension bezeichnet.

H.G. Wells, Die Zeitmaschine und Von kommenden Tagen, Wien, Hamburg 1980, S. 8/9.

H.G. Wells, Das Kristall-Ei. Erzählungen, Wien, Hamburg 1979, S. 156–157.

Ein Mathematiker bekannte, dass ein Möbiusband einseitig ist und dass man Heiterkeit erntet, wenn man es halbiert; bleibt es doch eins, obwohl geteilt.

H.G. Wells, Der Unsichtbare, Wien 1981, S. 145.

Linda Dalrymple Henderson, The Fourth Dimension and Non-Euclidean Geometry in Modern Art, Princeton 1983, S. XXI.

Bei Henderson heißt es: «Die vierte Dimension zog die Aufmerksamkeit von Literaten wie H.G. Wells, Oscar Wilde, Joseph Conrad, Ford Madox Ford, Marcel Proust und Gertrude Stein auf sich. Auch Musiker wie Alexander Scriabin, Edgar Varese und George Antheil nahmen an der vierten Dimension lebhaftes Interesse und ließen sich von dieser höheren Wirklichkeit zu kühnen Neuerungen anregen» (a.a.O., S. XIX–XX).

Lenins Schrift Materialismus und Empiriokritizismus ist noch heute von so großer Bedeutung, weil sie das wissenschaftliche Denken der Sowjetunion und Osteuropas so tiefgreifend beeinflusst hat. Beispielsweise brachte Lenin mit der berühmten Wendung von der «Unerschöpflichkeit des Elektrons» die dialektische Vorstellung zum Ausdruck, dass wir bei unserem Vordringen ins Innere der Materie auf immer neue Ebenen und Widersprüche stoßen werden. So sind Galaxien aus kleineren Sternensystemen zusammengesetzt, die ihrerseits Planeten enthalten, die aus Molekülen bestehen, deren Bausteine Atome sind, die Elektronen enthalten, die wiederum «unerschöpflich» sind. Das ist eine Spielart der «Welten-in-Welten»-Theorie.

Wladimir I. Lenin, Materialismus und Empiriokritizismus, Werke, Bd. 14, Berlin 1971, S. 179.

A.a.O., S. 178.

Zitiert in: Rucker, Fourth Dimension, S. 64.

Robert Heinlein, Das 4-D-Haus, in: ders., Entführung in die Zukunft, München 1971.

Stellen wir uns einen Flachländer vor, der eine Sequenz von sechs aneinander angrenzenden Quadraten in Form eines Kreuzes herstellt. Für den Flachländer sind die Quadrate starr. Sie lassen sich an keiner der Seiten, die die Quadrate verbinden, biegen oder drehen. Stellen wir uns jetzt aber vor, wir ergriffen die Quadrate und beschlössen, das Netz von Quadraten so zu falten, dass ein Würfel entstünde. Die Gelenkstellen zwischen den Quadraten, die in zwei Dimensionen starr sind, lassen sich in drei Dimensionen leicht falten. Tatsächlich vollzöge sich der Faltvorgang so mühelos, dass ein Flachländer ihn noch nicht einmal bemerken würde. Wenn sich nun ein Flachländer im Inneren des Würfels befände, würde er eine überraschende Entdeckung machen: Jedes Quadrat führt zu einem anderen Quadrat. Der Würfel hätte kein «Außen». Jedes Mal, wenn der Flachländer sich von einem Quadrat ins nächste begäbe, vollführte er eine unmerkliche Wendung von 90 Grad in der dritten Dimension und beträte das nächste Quadrat. Von außen betrachtet, wäre das Haus nur ein gewöhnliches Quadrat. Doch jemand, der das Quadrat beträte, fände eine bizarre Folge von Quadraten vor, von denen jedes auf unmögliche Weise in das nächste führte. Ihm erschiene unmöglich, dass das Innere eines einzigen Quadrates eine Sequenz von sechs Quadraten beherbergte.

Albrecht Fölsing, Albert Einstein, Frankfurt/Main 1993, S. 33.

Jacob Bronowski, Der Aufstieg des Menschen, Frankfurt/Main, Berlin, S. 248.

Albert Einstein, Autobiographisches, in: Paul Arthur Schilpp (Hg.), Albert Einstein als Philosoph und Naturforscher, Braunschweig 1979, S. 20.

Entsprechend wären die Insassen des Zugs der Meinung, der Zug befände sich in Ruhe und die U-Bahn-Station käme auf sie zu. Sie nähmen den Bahnsteig und all die auf ihm wartenden Menschen zusammengedrückt wie ein Akkordeon wahr. Das führt uns zu der widersprüchlichen Schlussfolgerung, dass sowohl die Reisenden im Zug als auch die Menschen auf dem Bahnsteig jeweils von den anderen denken, sie seien zusammengepresst. Die Auflösung dieses Paradoxons ist schwierig.*

* Normalerweise ist die Vorstellung absurd, von zwei Menschen könnte jeder größer als der andere sein. Doch in dieser Situation haben wir zwei Menschen, von denen jeder zu Recht meint, der andere sei zusammengestaucht. Das ist kein echter Widerspruch, weil es Zeit kostet, eine Messung vorzunehmen, und die Zeit ebenso wie der Raum verformt ist. Vor allem sind Ereignisse, die in einem Bezugssystem gleichzeitig erscheinen, in einem anderen Bezugssystem beobachtet, nicht gleichzeitig.

Nehmen wir beispielsweise an, Menschen auf dem Bahnsteig holen ein Lineal hervor und lassen den Messstab beim Vorbeifahren des Zuges auf den Bahnsteig fallen. Während der Zug vorbeifährt, lassen sie den Stab los, sodass die Enden gleichzeitig auf dem Bahnsteig auftreffen. So können sie beweisen, dass die Gesamtlänge des zusammengepreßten Zuges, von der Spitze bis zum Ende, nur dreißig Zentimeter lang ist.

Betrachten wir den gleichen Messvorgang nun vom Standpunkt der Passagiere im Zug. Sie denken, sie sind in Ruhe und sehen die zusammengepresste U-Bahn-Station auf sich zukommen, in der zusammengestauchte Menschen sich anschicken, ein zusammengestauchtes Lineal auf den Bahnsteig fallen zu lassen. Zunächst scheint es unmöglich, dass ein so winziges Lineal in der Lage ist, die Gesamtlänge des Zuges zu messen. Doch wenn das Lineal fallengelassen wird, treffen seine Enden nicht gleichzeitig auf dem Bahnsteig auf. Ein Ende des Lineals schlägt genau zu dem Zeitpunkt auf dem Boden auf, da die Station die Spitze des Zuges passiert. Doch erst als die Station sich an dem ganzen Zug vorbeibewegt hat, schlägt auch das zweite Ende des Lineals auf dem Boden auf. Dergestalt misst ein und dasselbe Lineal die Gesamtlänge des Zuges in beiden Bezugssystemen.

Das Wesen dieses «Paradoxons» und vieler anderer, die in der Relativitätstheorie auftreten, liegt darin, dass der Messvorgang Zeit in Anspruch nimmt und dass Raum wie Zeit auf verschiedene Arten in verschiedenen Bezugssystemen verzerrt werden.

Maxwells Gleichungen sehen wie folgt aus (wir setzen c = 1):

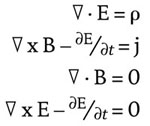
Die zweite und letzte Zeile sind Vektorgleichungen, die jeweils für die Gleichungen stehen. Tatsächlich handelt es sich also bei den Maxwell’schen Gleichungen um acht.

Diese Gleichungen können wir relativistisch umformen. Wenn wir den Maxwell’schen Tensor 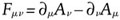einführen, dann reduzieren sich diese Gleichungen auf eine einzige:

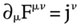
Sie ist die relativistische Version der Maxwell’schen Gleichungen.

Zitiert in: Pais, Raffiniert ist der Herrgott, S. 240.

A.a.O., S. 176.

Stellen Sie sich beispielsweise vor, Sie wären ein Rettungsschwimmer am Strand und befänden sich in einiger Entfernung vom Wasser. Aus den Augenwinkeln sehen Sie, dass jemand draußen auf dem Meer ertrinkt, und zwar ein ganzes Stück seitwärts versetzt von Ihnen. Nehmen wir an, Sie können im tiefen Sand nur langsam laufen, aber im Wasser sehr rasch schwimmen. Der Weg der schnellsten Ankunft ist dann eine gekrümmte Linie: Sie reduziert die Zeit, die Sie durch den Sand rennen müssen, und maximiert die Zeit, die Sie im Wasser schwimmen.

Einsteins Gleichungen sehen wie folgt aus:

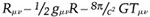
wobei T_μν der Impuls-Energie-Tensor ist, der den Materie-Energie-Gehalt misst, während R_μν der verjüngte Riemann’sche Krümmungstensor ist. Diese Gleichung besagt, dass der Impuls-Energie-Tensor das Ausmaß der Krümmung im Hyperraum bestimmt.

Zitiert in: Pais, Raffiniert ist der Herrgott, S. 213.

Zitiert in: K.C. Cole, Sympathetic Vibrations: Reflections on Physics as a Way of Life, New York 1985, S. 29.

Eine Hyperkugel lässt sich weitgehend ebenso definieren wie ein Kreis oder eine Kugel. Ein Kreis wird definiert als die Menge der Punkte, die der Gleichung x² + y² = r² in der x-y-Ebene genügen. Eine Kugel wird definiert als die Menge der Punkte, die x² + y² + z² = r² im x-y-z-Raum genügen. Entsprechend wird eine vierdimensionale Hyperkugel als die Menge der Punkte definiert, die x² + y² + z² + u² = r² im x-y-z-u-Raum genügen. Dieses Verfahren lässt sich leicht auf einen n-dimensionalen Raum erweitern.

Zitiert in: Abdus Salam, Overview of Particle Physics, in: Paul Davies (Hg.), The New Physics, Cambridge 1989, S. 487.

Theodor Kaluza, Zum Unitätsproblem der Physik, in: Sitzungsberichte Preußische Akademie der Wissenschaften, 96, 1921, S. 69.

1914, noch bevor Einstein seine allgemeine Relativitätstheorie vorschlug, versuchte der Physiker Gunnar Nordström, Elektromagnetismus und Gravitation durch Einführung einer fünfdimensionalen Maxwell-Theorie zu vereinigen. Ein näherer Blick auf diese Theorie zeigt, dass sie in vier Dimensionen eine korrekte Wiedergabe der Maxwell’schen Lichttheorie liefert, dass sie aber eine Skalartheorie der Gravitation darstellt, von der wir wissen, dass sie falsch ist. Infolgedessen gerieten Nordströms Ideen weitgehend in Vergessenheit. In gewissem Sinne hat er sich zu früh zu einer Veröffentlichung entschlossen. Er schrieb seinen Artikel ein Jahr, bevor Einsteins Gravitationstheorie veröffentlicht wurde, und deshalb war es ihm unmöglich, eine fünfdimensionale Gravitationstheorie vom Einstein-Typus zu entwickeln.

Im Gegensatz zu Nordströms Vorschlag begann Kaluzas Theorie mit einem Maßtensor g_μν, der im fünfdimensionalen Raum definiert ist. Dann setzte Kaluza g_μν mit dem Maxwell’schen Tensor A_μ gleich. Einsteins alte vierdimensionale Metrik entsprach Kaluzas neuer Metrik nur, wenn μ und ν nicht gleich 5 waren. Durch diese einfache, aber elegante Verfahrensweise wurden sowohl das Einstein’sche als auch das Maxwell’sche Feld in Kaluzas fünfdimensionalem Maßtensor untergebracht.

Offenbar haben auch Heinrich Mandel und Gustav Mie fünfdimensionale Theorien vorgeschlagen. Wahrscheinlich hat der Umstand, dass höhere Dimensionen eine so beherrschende Rolle in der öffentlichen Vorstellung spielten, auf die physikalische Welt zurückgewirkt. Insofern fand Riemanns Arbeit hier ihre Vollendung.

Peter Freund, im Gespräch mit dem Autor, 1990.

Ebenda.

Zitiert in: K.C. Cole, Sympathetic Vibrations: Reflections on Physics as a Way of Life, New York 1985, S. 204.

Zitiert in: Nigel Calder, The Key to the Universe, New York 1986, S. 326.

Zitiert in: R.P. Crease und C.C. Mann, The Second Creation, New York 1986, S. 326.

A.a.O., S. 293.

«Tiger! Tiger! Helles Brennen in den Wäldern der Nacht. Wes Unsterblichen Hand oder Auge konnte deine fürchterliche Symmetrie bilden?», William Blake, Tyger! Tyger! burning bright, aus: Songs of Experience, in: W.B. Yeats (Hg.), The Poems of William Blake, London 1905.

Zitiert in: Heinz Pagels, Die Zeit vor der Zeit. Das Universum bis zum Urknall, Berlin 1987, S. 195f.

Zitiert in: Cole, Sympathetic Vibrations, S. 229.

SU steht für «spezielle unitäre» Matrizen, das heißt Matrizen, die eine Einheitsdeterminante haben und unitär sind.

Zitiert in: John Gribbin, Auf der Suche nach Schrödingers Katze, München 1988, S. 93.

Halbwertszeit ist der Zeitraum, den die Hälfte des Stoffes braucht, um zu zerfallen. Nach zwei Halbwertszeiten ist nur noch ein Viertel des Stoffes übrig.

Zitiert in: Crease und Mann, The Second Creation, S. 411.

Zitiert in: Calder, The Key to the Universe, S. 15.

Zitiert in: Crease und Mann, The Second Creation, S. 418.

Pagels, Die Zeit vor der Zeit, S. 350.

«Steve Weinberg, aus Texas zurück, verblüfft uns mit Dimensionen überreichlich. Doch alle, die zusätzlich, sind zu einer Kugel aufgerollt, so winzig, dass sie uns nie betrifft», zitiert in: Crease und Mann, The Second Creation, S. 417.

Peter van Nieuwenhuizen, ‹Supergravity›, in: M. Jacob (Hg.), Supersymmetrie and Supergravity, Amsterdam, North Holland, 1986, S. 794.

Zitiert in: Crease und Mann, The Second Creation, S. 419.

Zitiert in: K.C. Cole, A Theory of Everything, in: New York Times Magazine, 18. Oktober 1987, S. 20.

John Horgan, The Pied Piper of Superstrings, in: Scientific American, November 1991, S. 42, 44.

Zitiert in: Cole, Theory of Everything, S. 25.

Edward Witten, Interview, in: Paul Davies und J. Brown (Hg.), Superstrings: Eine allumfassende Theorie der Natur in der Diskussion, München 1992, S. 116.

David Gross, Interview, in: Davies und Brown (Hg.), Superstrings, S. 181.

Witten, Interview, in: a.a.O., S. 121. Er betont, Einstein sei bei der allgemeinen Relativitätstheorie von einem physikalischen Prinzip ausgegangen, dem Äquivalenzprinzip (nach dem die schwere und die träge Masse eines Objektes gleich sind, sodass alle Körper, ganz gleich wie groß, gleich schnell zur Erde fallen). Das Gegenstück zum Äquivalenzprinzip hat man für die Stringtheorie noch nicht gefunden.

Witten: «Seit einigen Jahren ist klar, dass die Stringtheorie tatsächlich einen logisch konsistenten Rahmen bildet, der sowohl die Gravitation als auch die Quantenmechanik einschließt. Gleichzeitig jedoch ist das für ein wirkliches Verständnis der Theorie erforderliche Begriffssystem noch nicht entwickelt, wie es in Einsteins Gravitationstheorie beispielsweise durch das Äquivalenzprinzip repräsentiert wird» (a.a.O., S. 124).

Aus diesem Grund arbeitete Witten an sogenannten topologischen Feldtheorien – das heißt Theorien, die völlig unabhängig sind von der Art und Weise, wie wir Entfernungen messen. Dabei hoffte er, diese topologischen Feldtheorien könnten irgendeiner «ungebrochenen Phase der Stringtheorie» entsprechen – das heißt der Stringtheorie jenseits der Planck’schen Länge.

Gross, Interview, in: Davies und Brown (Hg.), Superstrings, S. 181.

Horgan, Pied Piper of Superstrings, S. 42.

Betrachten wir die Kompaktifizierung im Rahmen des vollständigen heterotischen Strings, der zwei Schwingungsmoden kennt: eine Schwingung in der Raumzeit mit allen 26 Dimensionen und die andere in der üblichen zehndimensionalen Raumzeit. Da 26 – 10 = 16 ist, nehmen wir an, dass sich 16 der 26 Dimensionen aufgewickelt haben – das heißt, zu irgendeiner Mannigfaltigkeit «kompaktifiziert» worden sind –, sodass wir eine zehndimensionale Theorie übrigbehalten. Jeder, der eine dieser 16 Richtungen einschlägt, kommt nicht vom Fleck.

Von Peter Freund stammt die Vermutung, dass die Symmetriegruppe des 16-dimensionalen kompaktifizierten Raums die Gruppe E(8) × E(8) sei. Eine rasche Überprüfung zeigt, dass diese Symmetrie erheblich größer ist und die Symmetriegruppe des Standardmodells – SU(3) × SU(2) × U(1) – einschließt.

Kurzum, die Schlüsselbeziehung ist 26 – 10 = 16, das heißt, wenn wir 16 der ursprünglich 26 Dimensionen des heterotischen Strings kompaktifizieren, bleibt uns ein kompakter 16-dimensionaler Raum und eine Restsymmetrie namens E(8) × E(8). Doch nach der Kaluza-Klein-Theorie muss ein Teilchen, wenn es gezwungen wird, sich in einem kompaktifizierten Raum aufzuhalten, zwangsläufig die Symmetrie dieses Raumes übernehmen. Das heißt, die Schwingungen des Strings müssen sich nach der Symmetriegruppe E(8) × E(8) ausrichten. Infolgedessen können wir den Schluss ziehen, dass diese Gruppe nach der Gruppentheorie weit größer als die Symmetriegruppe des Standardmodells ist und dass sie folglich das Standardmodell als kleine Teilmenge der zehndimensionalen Theorie einschließt.

Obwohl die Supergravitation in 11 Dimensionen definiert wird, ist sie immer noch zu klein, um alle Teilchenwechselwirkungen aufzunehmen. Die größte Symmetriegruppe für die Supergravitation ist O(8), die aber zu klein für die Symmetrien des Standardmodells ist.

Zunächst hat es den Anschein, als hätte die 11-dimensionale Supergravitation mehr Dimensionen und sei infolgedessen symmetrischer als die zehndimensionale Superstringtheorie. Doch das ist eine Illusion, weil der heterotische String den 26-dimensionalen Raum zu einem zehndimensionalen Raum kompaktifiziert, sodass wir 16 kompaktifizierte Dimensionen übrigbehalten, die die Gruppe E(8) × E(8) ergeben. Das ist mehr als genug, um das Standardmodell unterzubringen.

Witten, Interview, in: Davies und Brown (Hg.), Superstrings, S. 129.

Es sei angemerkt, dass auch andere nicht auf der Störungsrechnung beruhende Ansätze der Stringtheorie vorgeschlagen worden sind, doch sie sind nicht so weit gediehen wie die Stringfeldtheorie. Am ehrgeizigsten ist der «universelle Modularraum», mit dem man die Eigenschaften von Stringflächen mit einer unendlichen Zahl von Löchern zu untersuchen trachtet. (Leider kann niemand eine solche Fläche berechnen.) Ein anderer Ansatz ist die Renormierungs-Gruppen-Methode, die aber nur Flächen ohne Löcher (baumartige Diagramme) reproduzieren kann. Außerdem gibt es noch die Matrixmodelle, die sich bislang nur in zwei oder weniger Dimensionen definieren lassen.

Um diesen geheimnisvollen Faktor zwei zu verstehen, stellen wir uns einen Lichtstrahl vor, der zwei physikalische Schwingungsarten aufweist. Polarisiertes Licht kann, sagen wir, entweder horizontal oder vertikal schwingen. Dagegen hat ein relativistisches Maxwell-Feld A_μ vier Komponenten, wobei μ = 1, 2, 3, 4 ist. Bei Verwendung der Eichsymmetrie der Maxwell’schen Gleichungen dürfen wir zwei dieser vier Komponenten abziehen. Da 4 – 2 = 2 ist, haben sich die ursprünglichen vier Maxwell’schen Felder auf zwei reduziert. Genauso schwingt ein relativistischer String in 26 Dimensionen. Doch zwei dieser Schwingungsmoden lassen sich durch Symmetriebruch des Strings aufheben, sodass 24 Schwingungsmoden bleiben, eben jene, die in der Ramanujan-Funktion auftreten.

Zitiert in: Godfrey H. Hardy, Ramanujan, Cambridge 1940, S. 3.

Zitiert in: James Newman, The World of Mathematics, Bd. 1, Redmond, Wash. 1988, S. 363.

Hardy, Ramanujan, S. 9.

A.a.O., S. 10.

A.a.O., S. 11.

A.a.O., S. 12.

Jonathan Borwein und Peter B. Borwein, Srinivasa Ramanujan und die Zahl Pi, in: Spektrum der Wissenschaft, April 1988, S. 96.

David Gross, Interview, in: Paul Davies und J. Brown (Hg.), Superstrings, München 1992, S. 178.

Sheldon Glashow, Interactions, New York 1988, S. 335.

«Die Theorie für alles, räumt es doch ein, könnte mehr als nur ein String-Orbifold sein. Alt sind viele eurer Führer und sklerotisch, und sollten nicht allein verfügen über Sachen, die heterotisch. Laßt euch nicht blenden und hört unser Bitten, das Buch ist nicht fertig und das letzte Wort nicht Witten.» A.a.O., S. 333.

A.a.O., S. 330.

Steven Weinberg, Der Traum von der Einheit des Universums, S. 226.

«Blinke, blinke, kleiner Stern. Ich frag nicht, was du bist, denn nach spektroskopischem Erkenntnisstand, das weiß ich, bestehst du aus Wasserstoff.», zitiert in: John D. Barrow und Frank J. Tipler, The Anthropic Cosmological Principle, Oxford 1986, S. 327.

Zitiert in F. Wilczek und Devine, Longing for the Harmonies, New York 1988, S. 65.

«Neutrinos sind sehr klein, ganz ohne Ladung und Masse und wechselwirken nicht im Mindesten. Die Erde ist für sie nur eine tumbe Kugel, die sie einfach durchqueren wie Wollmäuse einen zugigen Flur oder Photonen eine Glasscheibe. Edelstem Gas zeigen sie die kalte Schulter, nehmen die solideste Mauer nicht zur Kenntnis, kümmern sich nicht um Stahl und tönenden Messing, fallen über den Hengst im Stall her und hohnlachen Klassenschranken, indem sie dich und mich durchdringen! Wie hohe und schmerzlose Guillotinen stürzen sie durch unsere Köpfe ins Gras. Bei Nacht fallen sie in Nepal ein und durchqueren den Burschen und sein Mädchen von der Unterseite des Bettes. Du nennst es wunderbar; für mich ist das ein starkes Stück.»

John Updike, Cosmic Gall, in: Telephone Poles and Other Poems, New York 1960.

Zitiert in: K.C. Cole, A Theory of Everything, in: New York Times Magazine, 18. Oktober, 1987, S. 28.

Zitiert in: Heinz Pagels, Zeit vor der Zeit. Das Universum bis zum Urknall, Berlin 1987, S. 27.

Zitiert in: K.C. Cole, Sympathetic Vibrations: Reflections on Physics as a Way of Life, New York 1985, S. 225.

Zitiert in:  Harrison, Masks of the Universe, New York 1985, S. 211.

Zitiert in: Corey S. Powell, The Golden Age of Cosmology, in: Scientific American, Juli 1992, S. 17.

Tatsächlich verdankt die Orbifold-Theorie ihre Entstehung mehreren Wissenschaftlern, darunter L. Dixon, J. Harvey und Edward Witten aus Princeton.

Vor Jahren haben sich Mathematiker eine einfache Frage gestellt: Wie viele Schwingungsarten können auf einer im n-dimensionalen Raum gekrümmten Fläche existieren? Nehmen wir beispielsweise Sand, den man auf eine Trommel rieseln lässt. Schwingt die Trommel in einer bestimmten Frequenz, so tanzen die Sandkörner auf der Trommelfläche und bilden Muster von wunderbarer Symmetrie. Verschiedene Muster der Sandkörner entsprechen verschiedenen Frequenzen, die auf der Trommelfläche möglich sind. In ähnlicher Weise haben Mathematiker die Zahl und die Arten von Schwingungen errechnet, die auf einer im n-dimensionalen Raum gekrümmten Fläche möglich sind. Sie haben sogar die Schwingungen berechnet, die ein Elektron auf einer solchen hypothetischen Fläche haben könnte. Für die Mathematiker war dies eine hübsche geistige Übung. Niemand glaubte damals, es könnte irgendeine physikalische Anwendungsmöglichkeit geben. Schließlich, so meinten sie, schwingen Elektronen nicht auf n-dimensionalen Flächen.

Dieser umfangreiche Bestand an mathematischen Sätzen lässt sich nun auf das Problem der GUT-Familien anwenden. Jede GUT-Familie muss, wenn die Stringtheorie stimmt, Resultat irgendeiner Schwingung auf einem Orbifold sein. Da die Mathematiker die verschiedenen Schwingungsarten katalogisiert haben, brauchen die Physiker nur noch in einem Mathematikbuch nachzusehen, wie viele identische Familien es gibt. Damit ist der Ursprung des Familienproblems die Topologie. Ist die Stringtheorie richtig, so lässt sich die Herkunft dieser drei gleichen Familien von GUT-Teilchen nicht verstehen, wenn wir unser Bewusstsein nicht auf zehn Dimensionen erweitern.

Sobald wir die unerwünschten Dimensionen zu einer winzigen Kugel aufgerollt haben, können wir die Theorie mit den Experimentaldaten vergleichen. Beispielsweise entspricht der niedrigste Erregungszustand des Strings einem geschlossenen String mit einem sehr kleinen Radius. Die Teilchen, die bei der Schwingung eines kleinen geschlossenen Strings auftreten, sind exakt diejenigen, die wir aus der Supergravitation kennen. So gelangen wir zu all den guten Ergebnissen der Supergravitation, während wir die schlechten vermeiden. Die Symmetriegruppe dieser neuen Supergravitation ist E(8) × E(8) und damit weit größer als die Symmetrie des Standardmodells oder auch der GUT-Theorie. Folglich enthält der Superstring sowohl die GUT als auch die Supergravitation (ohne viele der schlechten Eigenschaften beider Theorien). Statt seine Rivalen aus dem Weg zu räumen, frisst der Superstring sie einfach auf.

Allerdings werfen diese Orbifolds auch ein Problem auf: Wir können Hunderte und Tausende von ihnen konstruieren. Es gibt sie in höchst unangenehmem Überfluss. Jeder von ihnen beschreibt im Prinzip ein in sich schlüssiges Universum. Wie sollen wir nun entscheiden, welches Universum das richtige ist? Unter diesen Tausenden von Lösungen finden sich viele, die exakt die drei Generationen oder Familien von Quarks und Leptonen beschreiben. Wir können also Tausende von Lösungen finden, in denen es viel mehr als drei Generationen gibt. Während also in den GUTs drei Generationen als zu viel gelten, sind für viele Lösungen der Stringtheorie drei Generationen zu wenig.

David Gross, Interview, in: Paul Davies und J. Brown (Hg.), Superstrings, München 1992, S. 172f.

A.a.O., S. 173.

Genauer: Nach dem Pauli’schen Ausschließungsprinzip können zwei Elektronen nicht den Quantenzustand mit den gleichen Quantenzahlen innehaben. Das heißt, ein weißer Zwerg läßt sich als Fermi-Meer oder Elektronengas approximieren, das dem Pauli-Prinzip gehorcht.

Da sich Elektronen nicht im gleichen Quantenzustand befinden können, hindert sie eine resultierende Abstoßungskraft daran, zu einem Punkt zusammengepresst zu werden. In einem weißen Zwergstern hält letztlich diese Abstoßungskraft der Gravitation stand.

Die gleiche Logik gilt auch für die Neutronen in einem Neutronenstern, da Neutronen dem Pauli’schen Ausschließungsprinzip ebenfalls gehorchen, obwohl die Berechnung komplizierter ist.

Er schrieb: «Wenn der halbe Durchmesser einer Kugel von der Dichte der Sonne deren halben Durchmesser im Verhältnis 500 zu 1 überträfe, hätte ein Körper, der aus unendlicher Höhe fiele, an der Oberfläche dieser Kugel eine Geschwindigkeit angenommen, die größer als die des Lichtes wäre, und vorausgesetzt, das Licht würde wie andere Körper von einer Kraft im Verhältnis zu seiner vis inertiae angezogen, müsste alles Licht, das von einem solchen Körper emittiert würde, von der Schwerkraft wieder zurückgezwungen werden.»

John Michell, in: Philosophical Transactions of the Royal Society, 74, 1784, S. 35.

Zitiert in: Heinz Pagels, Zeit vor der Zeit. Das Universum bis zum Urknall, Berlin 1987, S. 75.

«Es war mal eine junge Dame namens Bright, die war viel schneller als das Licht. Eines Tages brach sie auf, nach relativistischer Weise, und kehrte in der Nacht davor zurück.»

Zitiert in: Anthony Zee, Fearful Symmetry, New York 1986, S. 68.

In: Anthony Boucher (Hg.), Science Fiction Stories, München 1964.

K. Gödel, An Example of a New Type of Cosmological Solution of Einsteins Field Equatations of Gravitation, in: Reviews of Modern Physics, 21, 1949, S. 447.