Impressum

Veröffentlicht im Rowohlt Verlag, Reinbek bei Hamburg, November 2018

Copyright © 2018 by Rowohlt Verlag GmbH, Reinbek bei Hamburg

Dieses Werk ist urheberrechtlich geschützt, jede Verwertung bedarf der Genehmigung des Verlages

Die englische Originalausgabe erschien 2017 bei Profile Books Ltd., London, unter dem Titel «Significant Figures. Lives and Works of Trailblazing Mathematicans» Copyright © Joat Enterprises, 2017

Fachlektorat Bernd Schuh

Umschlaggestaltung ZERO Media GmbH, München

Umschlagabbildung FinePic®, München, Ann Ronan Pictures/Print Collector/Getty Images, Fine Art Images/Heritage Images/Getty Images, Hulton Archive/Getty Images

Schrift DejaVu Copyright © 2003 by Bitstream, Inc. All Rights Reserved.

Bitstream Vera is a trademark of Bitstream, Inc.

Abhängig vom eingesetzten Lesegerät kann es zu unterschiedlichen Darstellungen des vom Verlag freigegebenen Textes kommen.

ISBN Printausgabe 978-3-499-63394-2 (1. Auflage 2018)

ISBN E-Book 978-3-644-40464-9

www.rowohlt.de

Hinweis: Die angegebenen Seitenzahlen beziehen sich auf die Printausgabe.

ISBN 978-3-644-40464-9

Anmerkungen

Inhalt

Einleitung 9

1 Störe meine Kreise nicht • Archimedes von Syrakus 25

2 Meister des Weges • Liu Hui 43

3 Dixit Algorismi • Muhammad al-Chwarizmi 53

4 Erfinder des Unendlichen • Madhava 67

5 Glücksspieler und Astrologe • Girolamo Cardano 79

6 Der Letzte Satz • Pierre de Fermat 91

7 Das Weltsystem • Isaac Newton 107

8 Unser aller Meister • Leonhard Euler 129

9 Der Wärmeoperator • Joseph Fourier 145

10 Das unsichtbare Gerüst • Carl Friedrich Gauß 159

11 Die Regeln beugen • Nikolai Iwanowitsch Lobatschewski 179

12 Radikale und Revolutionäre • Évariste Galois 195

13 Die Zahlenzauberin • Augusta Ada King 213

14 Gesetze des Denkens • George Boole 229

15 Primzahl-Virtuose • Bernhard Riemann 249

16 Kardinal des Kontinuums • Georg Cantor 265

17 Die erste große Dame der Mathematik • Sofja Kowalewskaja 283

18 Die Ideen überstürzen sich • Henri Poincaré 301

19 Wir müssen wissen, wir werden wissen • David Hilbert 321

20 Einsturz der akademischen Ordnung • Emmy Noether 337

21 Der Formelmann • Srinivasa Ramanujan 353

22 Unvollständig und unentscheidbar • Kurt Gödel 373

23 Die Maschine stoppt • Alan Turing 387

24 Vater der Fraktale • Benoit Mandelbrot 405

25 Das Innere nach außen kehren • William Thurston 423

Mathematiker – Was macht sie so besonders? 439

Anhang

Anmerkungen 449

Weiterführende Literatur 453

Register 459

Einleitung

Alle Zweige der Naturwissenschaften können ihre Ursprünge weit ins Dunkel der Geschichte zurückverfolgen, doch bei den meisten Themen heißt es über die früheren Erkenntnisse: «Heute weiß man, dass das falsch war» oder «Sie waren schon auf dem richtigen Weg, doch heute sehen wir die Dinge anders». So nahm der griechische Philosoph Aristoteles zum Beispiel an, ein galoppierendes Pferd verliere niemals vollständig seinen Bodenkontakt, was Eadweard Muybridge 1878 mit Hilfe einer Reihe von Kameras, die durch quer zur Pferderennbahn gespannte Zugdrähte ausgelöst wurden, widerlegte. Aristoteles’ Bewegungstheorie wurde von Galileo Galilei und Isaac Newton vollständig widerlegt, und seine Theorie des Geistes steht in keinerlei nutzbarer Beziehung zu den modernen Neurowissenschaften und zur Psychologie.

Die Mathematik ist anders. Sie ist von Dauer. Als die alten Babylonier herausfanden, wie man quadratische Gleichungen löst – wahrscheinlich um 2000 v. Chr., auch wenn die erste belastbare Quelle aus der Zeit um 1500 v. Chr. datiert –, veraltete ihr Ergebnis niemals. Es stimmt heute ebenso wie damals. Wir drücken das Ergebnis symbolisch aus, doch die dahinter stehende Logik ist dieselbe. Es gibt eine durchgehende Linie mathematischen Denkens, die zurück bis nach Babylon reicht. Als Archimedes herausfand, wie sich das Volumen einer Kugel berechnen lässt, benutzte er keine algebraischen Symbole und er dachte nicht an eine spezifische Zahl π wie wir heute. Er drückte sein Ergebnis geometrisch aus, in Form von Verhältnissen, wie es damals bei den Griechen üblich war. Dennoch erkennt man sofort, dass seine Antwort unserer heutigen Darstellung πr³ entspricht.

Einige antike Entdeckungen außerhalb der Mathematik haben sich als ähnlich beständig erwiesen, z.B. das archimedische Prinzip, dem zufolge ein Objekt sein eigenes Gewicht an Flüssigkeit verdrängt, oder Archimedes’ Hebelgesetz. Auch Teile der griechischen Physik und der Ingenieurswissenschaften haben bis heute Bestand. Aber bei diesen Themen ist Langlebigkeit die Ausnahme, während es in der Mathematik eher die Regel ist. Euklids Elemente, die das logische Fundament der Geometrie entwerfen, lohnen noch immer eine nähere Beschäftigung. Ihre Sätze bleiben wahr, und viele bleiben auch nützlich. In der Mathematik kommen wir voran, ohne die Erkenntnisse unserer Geschichte zu verwerfen.

Bevor Sie nun auf den Gedanken kommen, dass die Mathematik nur rückwärts gewandt ist, möchte ich zwei Dinge betonen. Zum einen kann sich die vermeintliche Bedeutung einer Methode oder eines Theorems verändern. Ganze mathematische Gebiete sind aus der Mode gekommen oder obsolet geworden, wenn sich Grenzen verschoben oder neue Techniken entwickelt wurden. Aber sie sind noch immer wahr, und von Zeit zu Zeit erlebt ein schon abgeschriebenes Gebiet eine Renaissance – gewöhnlich aufgrund einer neu entdeckten Verbindung mit einem anderen Gebiet, einer neuen Anwendung oder eines methodologischen Durchbruchs. Zum anderen haben Mathematiker bei der Entwicklung ihrer Fragestellung nicht nur Fortschritte gemacht, sondern sie haben sich zudem eine riesige Menge an neuer, wichtiger, wunderbarer und nützlicher Mathematik ausgedacht.

Nichtsdestotrotz bleibt die grundsätzliche Aussage immer unangefochten. Sobald ein mathematischer Satz einmal korrekt bewiesen ist, wird er zu einem Stein, auf den wir bauen können – für immer. Auch wenn unser Konzept dessen, was wir als Beweis akzeptieren, seit Euklids Tagen beträchtlich strenger geworden ist, um uns von unbewiesenen Annahmen zu befreien, können wir das, was uns heute lückenhaft erscheint, ergänzen, und das Ergebnis steht noch immer.

Dieses Buch beschäftigt sich mit dem fast mythischen Prozess, durch den neue Mathematik entsteht. Mathematik entwickelt sich nicht im luftleeren Raum: Sie wird von Menschen geschaffen. Unter ihnen finden sich einige von erstaunlicher Originalität und Verstandesschärfe, die Menschen, die wir mit großen Durchbrüchen assoziieren – die Pioniere, die wegweisenden Figuren. Historiker betonen zu Recht, dass die Werke der Großen von einer riesigen Menge Unterstützer abhingen, die zahllose kleine Puzzleteile zum Gesamtbild beisteuerten. Wichtige oder fruchtbare Fragen können von relativ Unbekannten gestellt werden, wesentliche Ideen können von Menschen vage erfasst werden, denen die technischen Fähigkeiten fehlen, sie in mächtige neue Methoden oder Perspektiven zu verwandeln. Newton meinte einmal, er stünde «auf den Schultern von Riesen». Das klang in gewisser Weise sarkastisch; mehrere dieser «Riesen» (vor allem Robert Hooke) klagten, Newton stünde weniger auf ihren Schultern als auf ihren Zehen, weil er ihre Leistung nicht ausreichend würdige oder in der Öffentlichkeit allen Ruhm einstreiche, obwohl er ihre Beiträge in seinen Schriften zitiere. Dennoch hatte Newton recht mit seiner Aussage: Seine große Synthese von Bewegung, Schwerkraft und Licht basierte auf einer Vielzahl von Einsichten seiner intellektuellen Vorgänger. Doch sie waren nicht alle Riesen. Auch ganz gewöhnliche Leute spielten eine wichtige Rolle.

Dennoch ragen die Riesen heraus und schreiten voran, während wir Übrigen folgen. Mit Hilfe von Leben und Werk einer Auswahl bedeutender Persönlichkeiten können wir Einblick gewinnen, wie neue Mathematik entsteht, wer sie entstehen lässt und wer diese Menschen waren. Für mich sind sie nicht nur Pioniere, die uns die Richtung wiesen, sondern Wegbereiter, die Pfade durch das undurchdringliche Unterholz im Dschungel mathematischen Denkens schlugen. Sie verbrachten einen Großteil ihrer Zeit damit, sich durch Dornengestrüpp und Sümpfe zu kämpfen, doch von Zeit zu Zeit stießen sie auf einen geheimen Friedhof der Elefanten oder ein El Dorado, wo sie im Unterholz verborgene Schätze entdeckten. Sie drangen in Denkregionen vor, die für die Menschheit zuvor Terra incognita waren.

Tatsächlich schufen sie diese Regionen. Der mathematische Dschungel ist nicht dasselbe wie der Amazonas-Regenwald oder der kongolesische Urwald. Der mathematische Wegbereiter ist kein David Livingstone, der sich seinen Weg längs des Sambesi-Flusses erkämpft oder nach den Quellen des Nils sucht. Livingstone «entdeckte» Dinge, die schon da waren. Tatsächlich wussten die Einheimischen schon lange, dass es sie gab. In jenen Tagen übersetzten Europäer «entdecken» jedoch mit «Europäer machen andere Europäer auf Dinge aufmerksam, die sie gefunden haben». Mathematische Wegbereiter erkunden jedoch nicht einfach einen bereits existierenden Urwald. In gewissem Sinne schaffen sie diesen Urwald, während sie ihn erforschen, als ob neue Pflanzen neben ihrem Weg entstehen und rasch zu Setzlingen und dann zu mächtigen Bäumen werden. Es wirkt jedoch so, als habe es diesen Urwald bereits zuvor gegeben, weil man sich nicht aussuchen kann, welche Pflanzen auf einmal emporschießen. Man sucht sich zwar aus, wo man hintritt, aber man kann nicht beschließen, eine Gruppe Mahagoni-Bäume zu «entdecken», wenn sich herausstellt, dass man in einem Mangrovensumpf gelandet ist.

Das ist meines Erachtens die Quelle der noch immer populären platonischen Sicht mathematischer Ideen: dass mathematische Wahrheiten «tatsächlich» existieren, jedoch in einer idealen Form in einer Art paralleler Realität, die schon immer existiert hat und immer existieren wird. Dieser Sichtweise zufolge finden wir, wenn wir einen neuen Satz beweisen, nur etwas heraus, was schon die ganze Zeit da war. Meiner Meinung nach ergibt der Platonismus keinen buchstäblichen Sinn, doch er beschreibt den Prozess der mathematischen Forschung präzise. Man hat keine Wahl, das Einzige, was man tun kann, ist, den Baum zu schütteln und zu schauen, was herabfällt. In seinem Buch What is Mathematics, Really? offeriert Reuben Hersh eine realistischere Sicht der Mathematik: Es handelt sich um eine gemeinsames mentales menschliches Konstrukt. In dieser Hinsicht erinnert es stark an Geld. Geld lässt sich nicht «wirklich» mit Münzen oder Dollarnoten oder Zahlen in einem Computer gleichsetzen, es handelt sich um einen gemeinsamen Satz von Übereinkünften darüber, wie wir Metallstücke, Papierscheine und Zahlen in einem Computer füreinander oder für Waren eintauschen.

Hersh erzürnte einige Mathematiker, die sich an dem «menschlichen Konstrukt» störten und einwandten, Mathematik sei keineswegs willkürlich. Sozialer Relativismus kann ihr nichts anhaben. Das ist richtig, doch Hersh machte eindeutig klar, dass Mathematik kein beliebiges menschliches Konstrukt ist. Wir entschließen uns, uns mit Fermats letztem Satz zu beschäftigen, aber wir können nicht darüber entscheiden, ob er wahr oder falsch ist. Das menschliche Konstrukt, das wir Mathematik nennen, unterliegt einem rigiden System logischer Einschränkungen, und eine Erkenntnis wird dem Konstrukt nur dann zugeschlagen, wenn sie diesen Auflagen genügt. Potenziell erlauben uns diese Auflagen, Wahres von Falschem zu unterschieden, aber wir finden nicht heraus, welche Alternative die richtige ist, indem wir betonen, dass nur eine von beiden zutreffen kann. Die große Frage ist: welche? Ich habe inzwischen aufgegeben zu zählen, wie oft jemand ein kontrovers diskutiertes, von ihm ungeliebtes mathematisches Problem attackiert hat, indem er darauf verwies, dass Mathematik eine Tautologie ist: Alles Neue ist eine logische Konsequenz von Dingen, die wir bereits kennen. Ja, das stimmt. Das Neue steckt implizit im Alten. Aber die harte Arbeit kommt dann, wenn man versucht, es herauszuholen. Fragen Sie Andrew Wiles; es bringt nicht viel, ihm zu erklären, dass der Status von Fermats Letztem Satz durch die logische Struktur der Mathematik stets vorgegeben war. Er verbrachte sieben Jahre damit, herauszufinden, was dessen prädeterminierter Status tatsächlich ist. Bis man das tut, ist das Wissen darum, dass etwas prädeterminiert ist, etwa so nützlich, wie jemanden nach dem Weg zum Berliner Reichstag zu fragen und die Antwort zu erhalten, er befinde sich in Deutschland.

Dieses Buch ist keine systematische Geschichte der gesamten Mathematik, doch ich habe versucht, die angeschnittenen mathematischen Themen in kohärenter Weise darzulegen, sodass die Konzepte im Lauf des Buches systematisch aufeinander aufbauen. Ingesamt erfordert dies, alles in einer annähernd chronologischen Ordnung zu erzählen. Eine nach Themen geordnete Chronologie wäre unlesbar, weil wir dann ständig von einem Mathematiker zum anderen springen würden, daher habe ich die Kapitel nach Geburtsdaten geordnet und verweise gelegentlich auf Querverbindungen.[1]

Ich möchte Ihnen 25 bedeutende mathematische Persönlichkeiten vorstellen, aus der Antike bis in die Moderne, Männer und Frauen, aus dem Osten wie aus dem Westen. Ihre persönlichen Geschichten beginnen im alten Griechenland, und zwar mit dem großen Mathematiker und Ingenieur Archimedes, dessen Leistungen von der Approximation von π und der Berechnung von Fläche und Volumen einer Kugel bis zur archimedischen Schraube zum Heben von Wasser und einer kranartigen Maschine zur Zerstörung feindlicher Schiffe reichen. Es folgen drei Repräsentanten des Fernen Ostens, wo während des Mittelalters die wichtigsten mathematischen Fortschritte gemacht wurden: der chinesische Gelehrte Liu Hui, der persische Mathematiker Muhammad ibn Musa al-Chwarizmi, der die Begriffe «Algorithmus» und «Algebra» prägte, und der Inder Madhava aus Sangamagrama, der Pionierarbeit auf dem Gebiet unendlicher Reihen für die trigonometrischen Funktionen leistete, Reihen, die im Westen ein Jahrtausend später von Newton wiederentdeckt wurden.

Im Lauf der italienischen Renaissance verlagerte sich der Schwerpunkt der Mathematik wieder nach Europa; dort treffen wir auf Girolamo Cardano, einen der größten Gauner, die jemals das mathematische Pantheon geziert haben. Cardano, ein Spieler und Raufbold, schrieb einen der wichtigsten Texte über Algebra, die jemals gedruckt wurden, praktizierte Medizin und führte ein Leben wie aus der Regenbogenpresse. Zudem fertigte er Horoskope an. Im Gegensatz dazu war Pierre de Fermat, der durch seinen Letzten Satz berühmt wurde, ein Anwalt mit einer Leidenschaft für Mathematik, was oft dazu führte, dass er seine juristische Arbeit vernachlässigte. Er verwandelte die Zahlentheorie in einen anerkannten Zweig der Mathematik, leistete aber auch Beiträge zur Optik und entwickelte einige Vorläufer der Infinitesimalrechnung. Dieses Thema wurde von Newton vollendet. Sein Meisterwerk ist die Philosophiae Naturalis Principia Mathematica (Mathematische Prinzipien der Naturphilosophie), oft auch einfach Principia genannt. Darin legte er die Bewegungs- und Gravitationsgesetze dar und wandte sie auf die Bewegung des Sonnensystems an. Newton markiert einen Wendepunkt in der mathematischen Physik; er verwandelte sie in eine systematische mathematische Studie dessen, was er den «Aufbau der Welt» nannte.

Nach Newton verlagerte sich der Fokus der Mathematik von Großbritannien rund ein Jahrhundert lang nach Kontinentaleuropa und Russland. Leonhard Euler, der produktivste Mathematiker in der Geschichte, produzierte wichtige Schriften mit journalistischer Geschwindigkeit, während er gleichzeitig viele Gebiete der Mathematik in einer Reihe eleganter, klar geschriebener Lehrbücher systematisierte. Kein Bereich der Mathematik entging seiner strengen Prüfung. Euler nahm sogar einige Ideen von Joseph Fourier vorweg, dessen Untersuchung der Wärmeübertragung zu einer der wichtigsten Techniken im Handbuch der modernen Ingenieurswissenschaften führte: die Fourier-Analyse, die eine periodische Wellenform mit Hilfe der grundlegenden trigonometrischen Funktionen Sinus und Cosinus darstellt. Fourier war auch der Erste, der verstand, dass die Atmosphäre für den Wärmehaushalt der Erde eine wichtige Rolle spielt. Mit den einzigartigen Leistungen von Carl Friedrich Gauß, einem aussichtsreichen Kandidaten für den Titel des größten Mathematikers aller Zeiten, tritt die Mathematik ins moderne Zeitalter ein. Gauß begann mit der Zahlentheorie und festigte seinen Ruf als Astronom durch seine Vorhersage, der neu entdeckte Asteroid Ceres werde wiederauftauchen. Weiterhin erzielte er wichtige Fortschritte bei komplexen Zahlen, bei der Methode der kleinsten Quadrate und in der nichteuklidischen Geometrie, auch wenn er zum letzteren Thema nichts publizierte, weil er fürchtete, seine Ergebnisse seien der Zeit zu weit voraus und er würde sich damit nur lächerlich machen. Nikolai Iwanowitsch Lobatschewski war weniger zurückhaltend und publizierte zahlreiche Artikel über eine Alternative zur euklidischen Geometrie, die wir heute als hyperbolische Geometrie bezeichnen. Er und János Bolyai gelten heute als die rechtmäßigen Erfinder der nichteuklidischen Geometrie, die man als natürliche Geometrie einer Oberfläche mit konstanter Krümmung ansehen kann. Gauß hatte jedoch im Grunde recht, als er annahm, diese Idee sei ihrer Zeit voraus, und weder Lobatschewski noch Bolyai ernteten zu ihren Lebzeiten die verdiente Anerkennung. Wir beschließen diese Ära mit der tragischen Geschichte des Revolutionärs Évariste Galois, der mit nur 20 Jahren bei einem Duell, bei dem es um eine junge Frau ging, getötet wurde. Er leistete wertvolle Beiträge zur Algebra, die zur heutigen Charakterisierung des zentralen Konzepts der Symmetrie in Form von Transformationsgruppen führte.

Nun wird die Geschichte um ein neues Thema erweitert, um einen Weg, der von der ersten Mathematikerin geebnet wurde, die wir in diesem Buch treffen. Es geht um die Mathematik von Rechenautomaten. Augusta Ada King, Countess of Lovelace, war Mitarbeiterin von Charles Babbage, einem Mann, der nur ein einziges Ziel vor Augen hatte, da er die potenzielle Leistungsfähigkeit von Rechenmaschinen erkannt hatte. Er entwarf die Rechenmaschine Analytical Engine, einen Vorläufer des programmierbaren Computers aus Knarren und Zahnrädern, heute der Star der Steampunk-Science-Fiction. Ada gilt allgemein als erste Programmiererin, auch wenn diese Behauptung nicht unumstritten ist. Das Computerthema findet seine Fortsetzung in George Boole, der mit seiner Schrift An Investigation of The Laws of Thought einen mathematischen Formalismus für die digitale Logik heutiger Computer begründete.

Die Mathematik wird im Lauf der Zeit immer vielfältiger, und das gilt auch für unsere Geschichte, die in immer neue Regionen des üppig wuchernden Dschungels vordringt. Bernhard Riemann besaß die brillante Gabe, hinter scheinbar komplexen Konzepten einfache, allgemeine Ideen zu entdecken. Zu seinen Beiträgen zählen die Grundlagen der Geometrie, vor allem die gekrümmten «Mannigfaltigkeiten», auf denen Albert Einsteins revolutionäre Theorie der Gravitation, die Allgemeine Relativitätstheorie, aufbaut. Er machte aber auch große Fortschritte in der Primzahltheorie, indem er die Zahlentheorie durch seine «Zeta-Funktion» mit der komplexen Analysis verknüpfte. Die Riemann-Hypothese über die Nullstellen dieser Funktion ist eines der größten und wichtigsten ungelösten Probleme in der ganzen Mathematik, auf seine Lösung ist ein Preis von 1 Million Dollar ausgesetzt.

Als Nächster folgt Georg Cantor, der die Art und Weise veränderte, wie Mathematiker über die Grundlagen ihres Themas denken, indem er die Mengenlehre einführte und unendliche Entsprechungen der ganzen Zahlen 1, 2, 3… einführte. Das führte zu der Entdeckung, dass einige Unendlichkeiten größer sind als andere – und zwar in einem strengen, aussagekräftigen und nützlichen Sinn. Wie viele Neuerer wurde Cantor zu Lebzeiten missverstanden und verlacht.

Nun betritt unsere zweite Mathematikerin die Bühne, die außerordentlich begabte Sofja Kowalewskaja. Ihr Leben war ziemlich kompliziert in den Wirren der Russischen Revolution und erschwert durch die Hindernisse, die eine männerdominierte Gesellschaft intellektuell brillanten jungen Frauen in den Weg legte. Es ist erstaunlich, dass sie überhaupt irgendetwas in der Mathematik erreichte. Tatsächlich gelangen ihr bemerkenswerte Entdeckungen bei der Lösung von partiellen Differenzialgleichungen, der Bewegung starrer Körper, dem Aufbau der Saturnringe und der Lichtbrechung durch einen Kristall.

Die Geschichte gewinnt nun an Fahrt. Um die Wende vom 19. zum 20. Jahrhundert war der Franzose Henri Poincaré einer der weltweit führenden Mathematiker. Poincaré wirkte exzentrisch, war tatsächlich aber ungemein gescheit. Er erkannte die Bedeutung des gerade aufkommenden Gebiets der Topologie – der «Gummituchgeometrie», bei der sich Formen kontinuierlich verzerren lassen – und erweiterte sie von zwei auf drei Dimensionen und darüber hinaus. Bei der Untersuchung des Drei-Körper-Problems der Newton’schen Gravitation wandte er sie auf Differenzialgleichungen an. Das führte ihn zur Entdeckung des deterministischen Chaos, eines scheinbar zufälligen Verhaltens in einem nicht-zufälligen System. Beinahe hätte er auch die Spezielle Relativität entdeckt, bevor Einstein es tat.

Als deutsches Pendant zu Poincaré lernen wir David Hilbert kennen, dessen Karriere sich in fünf eigenständige Abschnitte unterteilt. Zunächst nahm er einen Gedankengang über «Invarianten» auf, der ursprünglich von Boole stammte; dabei handelt es sich um algebraische Ausdrücke, die trotz Koordinatenwechsel dieselben bleiben. Dann entwickelte er eine systematische Behandlung von Kerngebieten der Zahlentheorie. Anschließend nahm er sich Euklids geometrische Axiome vor, fand sie mangelhaft und fügte zusätzliche hinzu, um die logischen Lücken zu schließen. Als Nächstes beschäftigte er sich mit mathematischer Logik und den Grundlagen der Mathematik und initiierte ein Programm, um zu beweisen, dass sich die Mathematik auf eine axiomatische Basis stellen lässt, die sowohl konsistent (logisch widerspruchsfrei) als auch vollständig (jede Aussage kann entweder bewiesen oder widerlegt werden) ist. Und schließlich wandte er sich der mathematischen Physik zu und war nahe daran, Einstein bei der Allgemeinen Relativität zu schlagen; zudem führte er den Begriff des Hilbert-Raums ein, der für die Quantenmechanik eine zentrale Rolle spielt.

Emmy Noether ist unsere dritte und letzte Mathematikerin; sie lebte zu einer Zeit, als die meisten akademischen Platzhirsche die Teilnahme von Frauen am universitären Leben noch mehr oder minder vehement ablehnten. Sie begann wie Hilbert mit der Invariantentheorie und wurde später seine Mitarbeiterin. Hilbert bemühte sich sehr, die «gläserne Decke» zu zertrümmern und ihr eine akademische Dauerstellung zu verschaffen, teilweise mit Erfolg. Noether ebnete den Weg der abstrakten Algebra und leistete Pionierarbeit im Hinblick auf moderne axiomatische Strukturen wie Gruppen, Ringe und Felder. Sie bewies auch ein höchst wichtiges Theorem, das die Symmetrie physikalischer Gesetze zu Erhaltungsgrößen wie der Energie in Beziehung setzt.

Inzwischen ist die Geschichte im 20. Jahrhundert angelangt. Um zu zeigen, dass überragende mathematische Fähigkeiten sich nicht auf die gebildeten Klassen der westlichen Welt beschränken, folgen wir Leben und Karriere des autodidaktischen indischen Genies Srinivasa Ramanujan, der in Armut aufwuchs. Mit seiner frappierenden Fähigkeit, merkwürdige, aber richtige Gleichungen aus der Intuition zu entwickeln, konnten sich, wenn überhaupt, nur Giganten wie Euler und Carl Jacobi messen. Ramanujans Konzept eines Beweises war verschwommen, doch er konnte Gleichungen finden, von deren Existenz niemand anders auch nur geträumt hätte. Seine Unterlagen und Notizbücher werden noch immer auf neue und unverbrauchte Denkansätze hin durchforstet.

Zwei Mathematiker mit einer Neigung zum Philosophischen bringen uns zurück zu den Grundlagen des Themas und seiner Beziehung zu Computerberechnungen. Der eine ist Kurt Gödel, dessen Beweis, dass jedes beliebige Axiomensystem in der Arithmetik unvollständig und unentscheidbar sein muss, Hilberts Programm zerstörte, genau das Gegenteil zu beweisen. Der andere ist Alan Turing, der sich mit den Möglichkeiten eines programmierbaren Computers beschäftigte und dabei auf einen einfacheren und natürlicheren Beweis für Gödels Ergebnisse stieß. Turings Ruhm basiert natürlich darauf, dass es ihm im Zweiten Weltkrieg in Bletchley Park gelang, den Code der Enigma-Maschine zu knacken. Zudem entwickelte er den Turing-Test für künstliche Intelligenz und arbeitete nach dem Krieg an mathematischen Problemen in der Biologie, wie den Mustern von Fell- und Federzeichnungen. Er war homosexuell und starb unter tragischen und mysteriösen Umständen.

Ich habe mich entschieden, keine lebenden Mathematiker einzubeziehen und mit zwei zeitgenössischen Mathematikern zu schließen: ein reiner und ein angewandter Mathematiker (beide gleichermaßen unorthodox). Bei dem letzteren handelt es sich um Benoit Mandelbrot, der weithin für seine Arbeit über Fraktale bekannt wurde, geometrische Formen, die auf allen Vergrößerungsstufen eine detaillierte Struktur aufweisen. Fraktale können die Natur oft viel besser wiedergeben als traditionelle glatte Oberflächen wie Kugeln und Zylinder. Auch wenn mehrere andere Wissenschaftler an Strukturen arbeiteten, die wir heute als Fraktale ansehen, machte Mandelbrot einen großen Fortschritt, weil er ihr Potenzial als Modelle für die natürliche Welt erkannte. Er gehörte nicht zu dem Typ Mathematiker, die Theoreme beweisen; vielmehr besaß er ein intuitives visuelles Gespür für Geometrie, das ihm erlaubte, Beziehungen zu sehen und Vermutungen zu formulieren. Zudem hatte er durchaus Showtalent und konnte seine Ideen gut verkaufen. Das nahm ihm manch einer in der mathematischen Gemeinschaft übel, doch man kann es nicht jedem recht machen.

Zum Abschluss habe ich einen wirklich reinen Mathematiker gewählt, William Thurston. Auch Thurston verfügte über ein tiefes intuitives Gespür für Geometrie, und dies in einem breiteren und tieferen Sinn als Mandelbrot. Er konnte es mit jedem aufnehmen, wenn es um den Beweis von Theoremen ging, doch im Lauf seiner Karriere verlegte er sich immer stärker auf die Theoreme selbst und skizzierte die Beweise nur noch. Vor allem beschäftigte er sich mit Topologie, wo er auf unerwartete Verbindungen mit der nichteuklidischen Geometrie stieß. Schließlich motivierte dieser Kreis von Ideen Grigori Perelman, eine schwer fassbare Vermutung in der Topologie zu beweisen, die auf Poincaré zurückging. Seine Methoden bewiesen auch eine allgemeinere Vermutung Thurstons, die unerwartete Einblicke in alle dreidimensionalen Mannigfaltigkeiten gibt.

Im letzten Kapitel werde ich einige der roten Fäden aufgreifen, die sich durch die 25 Geschichten dieser erstaunlichen Männer und Frauen ziehen, und untersuchen, was sie uns über wegweisende Mathematiker lehren – wer sie sind, wie sie arbeiten, woher sie ihre verrückten Ideen beziehen und was sie überhaupt dazu treibt, sich mit Mathematik zu beschäftigen.

An dieser Stelle möchte ich jedoch zwei Warnungen aussprechen: Die erste ist, dass ich zwangsläufig selektiv vorgegangen bin. Der Platz reicht nicht aus, um umfassende Biographien zu liefern, einen Überblick über alles zu geben, an dem meine Pioniere und Pionierinnen arbeiteten, oder detaillierter zu beschreiben, wie sie zu ihren Ideen kamen und wie sie sich mit ihren Kollegen austauschten. Vielmehr habe ich versucht, dem Leser eine repräsentative Auswahl ihrer wichtigsten – oder interessantesten – Entdeckungen und Konzepte vorzustellen und dabei genügend historische Details einzuflechten, um ein Bild von ihnen als Menschen in ihrer jeweiligen Gesellschaft zu zeichnen. Bei einigen antiken Mathematikern muss selbst das sehr lückenhaft bleiben, denn nur wenige Berichte über ihr Leben (und oft kein Originaldokument ihrer Werke) haben bis in unsere Tage überdauert.

Die zweite Warnung ist, dass die 25 Mathematiker, die ich gewählt habe, keineswegs die einzigen bedeutenden Persönlichkeiten in der Entwicklung der Mathematik sind. Ich habe meine Wahl aus vielen Gründen getroffen – Bedeutung der Mathematik, intrinsisches Interesse für das Gebiet, menschlicher Reiz ihrer Geschichte, historische Periode, Vielfalt und diese so schwer fassbare Qualität «Ausgewogenheit». Wenn Ihr Lieblingsmathematiker fehlt, ist der wahrscheinlichste Grund dafür Platzmangel, gepaart mit dem Wunsch, Repräsentanten zu wählen, die in der dreidimensionalen Mannigfaltigkeit, deren Koordinaten Geographie, historische Periode und Geschlecht sind, breit gestreut sind. Ich glaube, dass jede Persönlichkeit in diesem Buch auf jeden Fall verdient, dort aufzutreten. Und ich bezweifle keinesfalls, dass viele andere mit dem gleichen Recht hätten ausgewählt werden können.

1. Störe meine Kreise nicht

Wir schreiben das Jahr 1973. Der Ort, an dem wir uns befinden, ist der Marinestützpunkt Skaramagas in der Nähe von Athen. Alle Augen sind auf die Sperrholzattrappe eines römischen Schiffes gerichtet. Ebenfalls auf das Schiffsmodell gerichtet sind die Strahlen der Sonne, die von siebzig kupferverkleideten Spiegeln in 50 Metern Entfernung – jeder einen Meter breit und einen halben Meter hoch – reflektiert werden.

Innerhalb weniger Sekunden fängt das Schiff Feuer.

Iannis Sakkas, ein zeitgenössischer griechischer Wissenschaftler, lässt damit ein möglicherweise mythisches Stück antiker griechischer Wissenschaft wiederaufleben. Im 2. Jahrhundert n. Chr. schrieb der römische Autor Lukian von Samosata, der Ingenieur und Mathematiker Archimedes habe bei der Belagerung von Syrakus um 214–212 v. Chr. eine Vorrichtung erfunden, um die feindlichen Schiffe durch Feuer zu zerstören. Ob es diese Vorrichtung jemals gab, und wenn ja, wie sie funktionierte, ist höchst umstritten. Lukians Bericht könnte sich ebenso auf den üblichen Einsatz von Brandpfeilen oder brennenden, von einem Katapult abgeschossenen Lumpen beziehen, doch es ist schwer vorstellbar, warum Lukian dies als neue Erfindung vorstellen sollte. Im 6. Jahrhundert vermutete der Mathematiker und Architekt Anthemios von Tralleis in seiner Schrift Brenngläser, dass Archimedes eine große Linse als Brennglas verwendet habe. Der am weitesten verbreiteten Version der Legende zufolge benutzte Archimedes jedoch einen riesigen Spiegel oder möglicherweise auch eine bogenförmig angeordnete Batterie von Spiegeln, um so etwas wie einen Parabol- oder Brennspiegel zu schaffen.

Die Parabel ist eine U-förmige Kurve, die den griechischen Geometern durchaus vertraut war. Archimedes kannte die geometrische Eigenschaft einer Parabel, parallel zu ihrer Achse einfallende Strahlen im Brennpunkt (Fokus) zu sammeln. Ob jemand damals allerdings erkannte, dass ein Parabolspiegel von der Sonne abgestrahltes Licht (und Wärmeenergie) auf dieselbe Weise fokussieren würde, ist weniger gewiss, denn das Verständnis der Griechen für Licht war noch schwach ausgeprägt. Doch Sakkas’ Experiment zeigt, dass Archimedes gar keine parabolische Anordnung gebraucht hätte. Eine größere Schar von Soldaten, jeder mit einem reflektierenden Schild bewaffnet, den er unabhängig von seinen Kameraden so ausrichtet, dass die zurückgeworfenen Sonnenstrahlen auf denselben Teil des feindlichen Schiffes fallen, wäre genauso effizient gewesen.

Über die Methode ist in der Vergangenheit heftig gestritten worden. Der Philosoph René Descartes, ein Pionier der Optik, glaubte nicht, dass die Sache hätte funktionieren können. Sakkas’ Experiment spricht hingegen dafür, dass es wohl möglich gewesen wäre, doch seine Sperrholzattrappe war ein Leichtbau und zudem mit einer Farbe auf Teerbasis angestrichen, also leicht entzündlich. Auf der anderen Seite war es zu Lebzeiten von Archimedes durchaus üblich, Schiffe mit Teerfarbe zu streichen, um ihren Rumpf zu schützen. Im Jahr 2005 wiederholte eine Gruppe von MIT-Studenten Sakkas’ Experiment, und es gelang ihnen schließlich, eine hölzerne Schiffsattrappe in Brand zu setzen – aber erst, nachdem sie die Sonnenstrahlen zehn Minuten auf das völlig still liegende Modell gebündelt hatten. Anschließend versuchten sie es erneut für die Fernsehsendung MythBusters, diesmal mit einem Fischerboot im Hafen von San Francisco; dabei gelang es ihnen zwar, das Holz zu verkohlen und ein paar Flammen zu erzeugen, doch das Boot entzündete sich nicht. MythBusters wertete den Versuch, die Legende zu belegen, daher als Fehlschlag.

Archimedes war ein Allround-Genie: Astronom, Ingenieur, Erfinder, Mathematiker und Physiker. Vermutlich war er (um den modernen Begriff zu verwenden) der größte Naturwissenschaftler seiner Zeit. Neben wichtigen mathematischen Entdeckungen gelangen ihm Erfindungen, die in ihrer Reichweite geradezu atemberaubend waren – die archimedische Schraube zur Förderung von Wasser, der Flaschenzug zum Heben schwerer Lasten – und er entdeckte das archimedische Prinzip schwimmender Körper sowie das Hebelgesetz (wenn auch nicht den Hebelapparat selbst, der schon viel früher eingesetzt wurde). Außerdem wird ihm eine zweite Kriegsmaschine zugeschrieben, die Kralle. Der Legende nach benutzte er diese kranartige Vorrichtung bei der Belagerung von Syrakus, um feindliche Schiffe aus dem Wasser zu heben und dann zu versenken. In der 2005 ausgestrahlten Fernsehdokumentation Superweapons of the Ancient World (etwa: Superwaffen der Antike) wurde eine eigene Version dieses Geräts gebaut, und es funktionierte. In antiken Texten finden sich noch viele weitere, Neugier weckende Hinweise auf Theoreme und Erfindungen, die Archimedes zugeschrieben werden. Darunter ist auch ein mechanisches Instrument zur Berechnung von Planetenbahnen, ganz ähnlich dem berühmten Antikythera-Mechanismus aus der Zeit um 100 v. Chr., der 1900–1901 in einem Schiffswrack entdeckt und dessen Funktion erst vor kurzer Zeit verstanden wurde.

Über Archimedes’ Leben ist nur wenig bekannt. Er wurde in Syrakus geboren, einer sizilianischen Stadt am südlichen Ende der Ostküste der Insel. Die Stadt wurde 734 oder 733 v. Chr. von griechischen Kolonisten gegründet, angeblich von dem halb mythologischen Archias, der Korinth verlassen und ins Exil gehen musste. Plutarch zufolge hatte sich Archias leidenschaftlich in den hübschen Knaben Actaeon verliebt. Als seine Werbung erfolglos blieb, versuchte er, den Knaben zu entführen, und bei dem sich daraufhin entwickelnden Handgemenge wurde Actaeon buchstäblich in Stücke gerissen. Der Ruf seines Vaters Melissus nach Gerechtigkeit fand vor Gericht jedoch kein Gehör, daher kletterte dieser auf die Spitze eines Poseidon geweihten Tempels, flehte den Gott an, seinen Sohn zu rächen, und stürzte sich auf die Felsen am Fuß des Tempels. Auf diese dramatischen Ereignisse folgten eine schwere Dürre und Hungersnot, und die Befragung des lokalen Orakels ergab, dass nur Vergeltung Poseidons Zorn besänftigen würde. Archias vernahm die Botschaft und ging, um seiner Opferung zu entgehen, freiwillig ins Exil nach Sizilien, wo er die Stadt Syrakus gründete. Später holte ihn seine Vergangenheit ein, und Telephus, der als Knabe ebenfalls das Opfer von Archias’ Begierde geworden war, brachte ihn um.

Das Land war fruchtbar, die einheimische Bevölkerung freundlich, und Syrakus stieg bald zu reichsten und mächtigsten griechischen Stadt im ganzen Mittelmeerraum auf. Im Sandrechner schreibt Archimedes, sein Vater sei Phidias, ein Astronom. In seinen vergleichenden Lebensbeschreibungen (Vitae parallelae) schreibt Plutarch, Archimedes sei ein entfernter Verwandter von Hieron II., dem Tyrannen von Syrakus, gewesen. Als junger Mann studierte Archimedes vermutlich in der ägyptischen Stadt Alexandria, die am Rand des Nildeltas direkt an der Mittelmeerküste liegt; dort lernte er vermutlich Konon von Samoa und Eratosthenes von Kyrene kennen. Zu den Indizien, die dafür sprechen, gehört Archimedes’ Aussage, Konon sei ein Freund gewesen; auch die Einleitungen seiner Bücher Die Methode der mechanischen Theoreme und Das Rinderproblem sind Eratosthenes gewidmet.

Es gibt auch einige Versionen über seinen Tod; darauf werden wir später noch zurückkommen.

Archimedes’ mathematische Reputation basiert auf denjenigen Werken, die bis in unsere Tage überdauert haben – alle als spätere Kopien seiner ursprünglichen Texte. Die Schrift Quadratur der Parabel, die als Brief an seinen Freund Dositheos verfasst wurde, enthält 24 Sätze (Theoreme) über Parabeln, wobei das letzte Theorem die Fläche eines Parabelsegments im Hinblick auf ein verwandtes Dreieck angibt. Die Parabel nimmt eine wichtige Stellung in seinem Werk ein. Es handelt sich um einen Typ des Kegelschnitts, eine Familie von Kurven, die in der griechischen Geometrie eine wichtige Rolle spielte. Ein Kegelschnitt entsteht, wenn man die Oberfläche eines Doppelkegels – also zwei identische, an der Spitze verbundene Kreiskegel – mit einer Ebene schneidet. Es gibt drei Haupttypen: die Ellipse, ein in sich geschlossenes Oval, die Parabel, eine U-förmige Kurve, und die Hyperbel, zwei U-förmige Kurven, die «Rücken an Rücken» stehen.

Archimedes’ Mechanik, auch Vom Gleichgewicht ebener Flächen, besteht aus zwei getrennten Büchern. Sie enthalten einige grundlegende Erkenntnisse über das Gebiet, das wir heute Statik nennen, also den Zweig der Mechanik, der die Bedingungen analysiert, unter denen ein Körper in Ruhe bleibt. Die Weiterentwicklung dieses Gebiets bildet das Fundament der gesamten Bauingenieurswissenschaften und ermöglicht es, die Kräfte zu berechnen, die auf die Strukturelemente von Bauwerken und Brücken einwirken, um sicherzustellen, dass sie tatsächlich stabil bleiben, statt einzuknicken oder zu kollabieren.

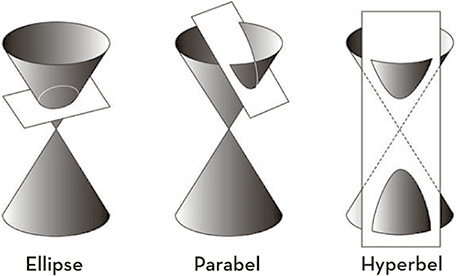
Die drei Haupttypen des Kegelschnitts.

Das erste Buch konzentriert sich auf das Hebelgesetz, das Archimedes so formuliert: «Lasten sind im Gleichgewicht, wenn ihre Hebelarme ihrem Gewicht umgekehrt proportional sind.» Eine Konsequenz daraus ist, dass ein langer Hebelarm eine kleine Kraft verstärkt. Wie Plutarch berichtet, drückte Archimedes diese Tatsache in einem Brief an König Hieron höchst dramatisch aus: «Gebt mir einen festen Punkt, und ich hebe die Welt aus den Angeln.» Er hätte einen sehr langen, völlig starren Hebel gebraucht, doch der größte Nachteil von Hebeln ist, dass die aufgewandte Kraft zwar verstärkt wird, das ferne Ende des Hebels aber eine viel kleinere Distanz zurücklegt als die Kraft. Archimedes hätte die Erde um dieselbe (sehr kleine) Entfernung allein durch Springen bewegen können. Nichtsdestotrotz ist ein Hebel ein höchst wirksames Gerät, und Gleiches gilt für eine Variante, die Archimedes ebenfalls gut verstand, den Flaschenzug:

Im zweiten Buch geht es hauptsächlich darum, den Schwerpunkt verschiedener geometrischer Formen – Dreieck, Parallelogramm und Parabelsegment – zu finden.

Die Abhandlung Über Kugel und Zylinder enthält Ergebnisse, auf die Archimedes so stolz war, dass er sie auf seinen Grabstein meißeln ließ. Er wies mathematisch streng nach, dass die Oberfläche einer Kugel viermal größer ist als die eines Großkreises (wie des Äquators einer kugelförmigen Erde), dass das Volumen einer Kugel zwei Drittel des Volumens eines Zylinders beträgt, der genau um die Kugel passt, und dass die Fläche eines beliebigen, durch eine Ebene ausgeschnittenen Kugelsegments gleich dem korrespondierenden Segment eines solchen Zylinders ist. Zum Beweis verwendete er ein umständliches Berechnungsverfahren, das als Exhaustionsmethode bezeichnet wird. Diese Methode wurde von Eudoxos eingeführt, um mit Volumen- und Flächenverhältnissen umzugehen, bei denen irrationale Zahlen eine Rolle spielen, die sich nicht in exakten Brüchen ausdrücken lassen. Modern ausgedrückt, bewies Archimedes, dass die Oberfläche einer Kugel mit dem Radius r gleich 4πr² ist und ihr Volumen πr³ beträgt.

Mathematiker sind es gewohnt, ihre auf Hochglanz polierten Endergebnisse in wunderbar organisierter Weise zu präsentieren, während sie den häufig umständlichen und mühseligen Prozess, der dazu geführt hat, unter den Tisch fallen lassen. Glücklicherweise erklärt uns Archimedes in seiner Methodenlehre genauer, wie er zu seinen Ergebnissen über die Geometrie der Kugel kam. Das Werk galt lange als verschollen, bis 1906 der dänische Mathematikhistoriker Johan Ludvig Heiberg eine unvollständige Kopie entdeckte, das Archimedes-Palimpsest. Ein Palimpsest ist eine beschriebene antike oder mittelalterliche Manuskriptseite, die durch Schaben oder Waschen gereinigt wurde, damit das Papier oder Pergament neu beschrieben werden konnte. Archimedes’ Werke wurden um 530 in Konstantinopel (heute Istanbul), der Hauptstadt des Byzantinischen Reiches, von Isidor von Milet zusammengetragen. Um 950 wurden diese Werke dann von einem byzantinischen Schreiber kopiert; damals leitete Leon der Mathematiker eine Schule, in der Archimedes’ Schriften studiert wurden. Das Manuskript gelangte schließlich nach Jerusalem, wo es 1229 auseinandergenommen, (nicht sehr effektiv) gewaschen, auf die Hälfte gefaltet und neu gebunden wurde, um daraus ein 177 Seiten starkes christliches Gebetbuch herzustellen.

In den 1840er Jahren stieß der evangelische Theologe Konstantin von Tischendorf in einer griechisch-orthodoxen Bibliothek auf den Text, der sich zu diesem Zeitpunkt wieder in Konstantinopel befand. Ihm fielen schwache Spuren griechischer Mathematik auf, und er nahm eine Seite mit nach Hause, die US