


DECISIONES
GERENCIALES
ESTRATÉGICAS:
UNA APLICACIÓN
A LA TEORÍA DE JUEGOS
2a EDICIÓN
Maximiliano González F.
Alexander Guzmán V.
María Andrea Trujillo D.
CESA - Colegio de Estudios Superiores de Administración
658.4012 / G659d 2017
González F., Maximiliano (Autor)
Decisiones gerenciales estratégicas: una aplicación a la teoría de juegos. 2a edición / Maximiliano González F., Alexander Guzmán V., María Andrea Trujillo D. (Autores). Bogotá: CESA–Colegio de Estudios Superiores de Administración. Editorial CESA, 2017. 338 p.
ISBN Impreso: 978-958-8999-14-6
ISBN Digital: 978-958-8988-15-3
Descriptores:
1. PLANIFICACIÓN ESTRATEGICA. 2. TEORÍA DE LOS JUEGOS
© 2017 CESA - Colegio de Estudios Superiores de Administración
© 2017 María Andrea Trujillo D. [Maria.trujillo@cesa.edu.co]
© 2017 Alexander Guzmán V. [Alexander.guzman@cesa.edu.co]
© 2017 Maximiliano González F. [Maxgonza@uniandes.edu.co]
ISBN Impreso: 978-958-8999-14-6
ISBN Digital: 978-958-8988-15-3
Editorial CESA
Casa Incolda
Diagonal 34a No 5a - 23
www.editorialcesa.com
www.cesa.edu.co
editorialcesa@cesa.edu.co
Grupo de Estudios en Administración
Proyecto de Investigación: Economía de la Información
Código interno: 10012
Bogotá, D.C, junio de 2017
Dirección Editorial: Editorial CESA
Corrección de estilo: José Ignacio Curcio
Diagramación y diseño: YO_Diseño
Desarrollo ePub: Lápiz Blanco S.A.S.
Todos los derechos reservados. Esta obra no puede ser reproducida sin el permiso previo escrito.
Impreso y hecho en Colombia
Agradecimientos
Prólogo
CAPÍTULO 1.
INTRODUCCIÓN Y EQUILIBRIO DE NASH
¿Qué es la teoría de juegos?
¿Qué hace que algo sea considerado un juego?
¿Cuál es el objetivo y la estructura de este libro?
Teoría de juegos y decisiones gerenciales
Estructura básica de un juego
Juegos estáticos de información completa y equilibrios
Aplicaciones
Problemas con solución para practicar y afianzar conceptos
CAPÍTULO 2.
ESTRATEGIAS MIXTAS
Interpretación de los equilibrios mixtos
Aplicaciones
Problemas con solución para practicar y afianzar conceptos
CAPÍTULO 3.
JUEGOS DINÁMICOS
Equilibrio Perfecto de Nash en Sub-juegos (EPNS)
¿Cómo transformar un juego dinámico en un juego estático?
Importancia de los juegos dinámicos
Aplicaciones
Problemas con solución para practicar y afianzar conceptos
CAPÍTULO 4.
JUEGOS REPETIDOS E INFORMACIÓN IMPERFECTA
Juegos repetidos finitos
Juegos repetidos infinitos
Aplicaciones
Juegos de información imperfecta
Problemas con solución para practicar y afianzar conceptos
CAPÍTULO 5
JUEGOS DE INFORMACIÓN INCOMPLETA
Actualización de creencias
Concepto de estrategia y equilibrio en los juegos bayesianos
Aplicaciones
Problemas con solución para practicar y afianzar conceptos
CAPÍTULO 6.
JUEGOS DE SEÑALES
Estructura básica de los juegos de señales
Aplicaciones
Problemas con solución para practicar y afianzar conceptos
CAPÍTULO 7.
OPCIONES REALES Y TOMA DE DECISIONES FINANCIERAS ESTRATÉGICAS
¿Qué es una opción real?
Clasificación de las opciones reales
Valoración de las opciones reales
Aplicaciones
Problemas con solución para practicar y afianzar conceptos
CAPÍTULO 8.
MINICASOS DE ESTUDIO
Caso de estudio 1.
Determinación de la política de precios
Caso de estudio 2.
Salida y entrada al mercado de explosivos para la minería en Colombia
Caso de estudio 3.
Política de cobranzas y descuentos por pronto pago
Caso de estudio 4.
Negociación con sindicatos
Caso de estudio 5.
Lucha entre banqueros
Caso de estudio 6.
Control corporativo, takeovers y el problema del “free-raider”
Caso de estudio 7.
Corrupción e incentivos
Caso de estudio 8.
Acceso al microcrédito
Caso de estudio 9.
Contratos como juegos de información incompleta
Caso de estudio 10.
Políticas de desarrollo como un juego de coordinación
Caso de estudio 11.
Empresa petrolera y sus opciones reales (parte A)
Caso de estudio 12.
Empresa petrolera y sus opciones reales (parte B)
Caso de estudio 13.
Empresa petrolera y sus opciones reales (parte C)
Bibliografía
Agradecemos especialmente a Diego Téllez, estudiante del doctorado en Administración de la Universidad de los Andes, la asistencia en la estructuración de la primera edición de este texto. Igualmente, reconocemos el aporte a la discusión y aplicación de la Teoría de Juegos a situaciones cotidianas de los estudiantes del curso Decisiones Gerenciales Estratégicas en el Magister en Administración, el Magister en Finanzas y la Maestría en Gerencia y Práctica del Desarrollo de la Facultad de Administración de la Universidad de los Andes. Finalmente, agradecemos la acogida de la Editorial CESA, y el proceso riguroso de evaluación que nos llevó a un mejor texto.
En mi práctica docente con empresarios y directivos he encontrado que la teoría de juegos es una excelente herramienta para incentivar el pensamiento estratégico. Sin duda una buena preparación en este campo es necesaria para quienes buscan ejercer cargos de dirección. Hay excelentes libros sobre el tema –como los que nos recomiendan los autores en las primeras páginas–, pero desafortunadamente muchos de los que se usan como textos en los cursos de la materia resultan complejos, abstractos y en cierta medida, difíciles de leer.
El presente texto apunta en una dirección muy interesante: mantener el rigor necesario para un grupo de estudiantes en formación, sin permitir que ese rigor se convierta en un obstáculo al entendimiento o el interés; vale decir, que la lectura juiciosa de este libro les permitirá conocer con cierta profundidad la teoría de juegos y los principios en que se sustenta, y les brindará multitud de oportunidades para aplicarlas a su vida gerencial y personal, sin que ello les exija una preparación matemática superior.
La teoría de juegos es cada vez más apreciada y su campo de aplicación crece en todas direcciones: economía, biología, psicología, negociación, politología, sociología, etc., por lo cual creo conveniente hacerle al lector dos advertencias.
La primera hace relación con lo que en teoría de juegos se denomina “pagos”, es decir, los números que acompañan a las matrices, y los árboles que encontrarán en este libro y en todo libro de teoría de juegos. Pero, ¿qué representan? Los pagos representan las preferencias del jugador: si el jugador tiene que elegir, elegirá la alternativa con el mayor pago (el número mayor en la matriz o en el árbol). ¿Y de dónde salen esos pagos? Simplificando en exceso se puede decir que se obtienen así: se le pregunta al jugador cuál alternativa, A o B, prefiere; si nos dice que prefiere B asignamos un pago de, por ejemplo, 1 a la alternativa B y un pago de 0 a la A. Así pues, ese 0 y ese 1 nos indican qué preferirá el jugador.
Naturalmente, cuando le llegue el momento a nuestro jugador de elegir entre la alternativa A y la B, podremos predecir que elegirá la B apoyados en que esta tiene un valor de 1, superior al valor de 0 de la alternativa A. Como se ve, se trata de una tautología: ¿por qué elige B?, porque tiene un valor mayor; ¿y por qué tiene un valor mayor?, porque nos dijo que esa sería la que elegiría.
Pero no por esto el lector debe creer que la teoría de juegos es simple, porque lo que resulta asombroso y apasionante es ver la cantidad de resultados sorprendentes que a partir de unas bases tan sencillas se pueden lograr. Tan sorprendentes que a veces nuestra intuición se revela, cuando no es la misma realidad la que lo hace. A esto, la teoría de juegos solo puede contestar que, si los pagos son los correctos y se presume racionalidad en los jugadores, el resultado es el que se indica, y que si el resultado no nos gusta o no se da en la realidad, debemos culpar a la mala asignación de los pagos, no a las conclusiones lógicas que obtiene la teoría.
A veces estos pagos no nacen de una pregunta directa, sino de una suposición como, por ejemplo, la de que frente a dos sumas de dinero el jugador preferirá la mayor. No es una mala suposición, pero los experimentos no se cansan de mostrar que los seres humanos, por múltiples razones, no siempre respondemos “lógicamente”, ni uniformemente, ni siquiera consistentemente. Esto, lejos de restarle belleza a la teoría, le agrega, creo, más asombro al conocimiento de nuestra condición de seres humanos.
La segunda advertencia tiene relación con lo que podríamos llamar la neutralidad ética de la teoría de juegos. Si bien esta teoría puede usarse, y se ha usado, para desarrollar teorías éticas, básicamente fundadas en el concepto de reciprocidad, muchas veces las recomendaciones de un análisis riguroso de una situación de juegos son inmorales y peligrosas. La carrera armamentista está muy bien justificada teóricamente, como puede estarlo la “guerra preventiva”, la aniquilación total del enemigo o, en un plano más cercano, y dadas ciertas circunstancias, la indiferencia, el abuso o la corrupción. No se trata solo de preocupaciones abstractas: los debates sobre armamentismo y ataques preventivos con armas nucleares se han sustentado en análisis incluso primitivos de teoría de juegos por personas de alto calibre intelectual.
La teoría de juegos se presenta como una herramienta interesantísima y enriquecedora, tanto, que es fácil dejarse deslumbrar. Los análisis y los ejemplos que están a punto de leer resultarán tan atractivos que correrán el peligro de intoxicarse con ellos. Tomada con la debida moderación, aplicada con la debida prudencia, la teoría de juegos puede ser una herramienta utilísima y hermosa, un mundo mágico y sorprendente que vale la pena conocer.
Agradezco a los autores por invitarme a prologar esta publicación, y los felicito por el trabajo desarrollado; al amable lector le deseo un viaje placentero y fructífero.
Ciro Gómez Ardila
Director Académico de INALDE Business School
Ph.D. en Management, IESE Business School
Master en Dirección de Empresas –MBA, INALDE Business School
Médico y Especialista en Anestesiología, Universidad del Rosario
Comencemos con un juego… hace un tiempo en Inglaterra un periódico anunció un concurso con las siguientes características: cada persona iba a enviar a la dirección del periódico una carta con su nombre y un número entero ente 1 y 100…, el ganador sería aquella persona cuyo número se aproximara más al promedio de todos los números recibidos dividido entre dos. Por ejemplo, si la persona A envió el número 60, la B el 50 y la C el 40, entonces el promedio es 50 y al dividirlo entre 2 el resultado es 25, y el ganador del concurso sería la persona C. Supongamos que hacemos ese concurso en un salón de clase y ofrecemos un premio de $1.000 (en la versión original el premio era 1.000 libras esterlinas!). ¿Qué cree que ocurriría? ¿Si usted estuviese en ese salón de clase, que número escribiría en el papel?
Nuestra experiencia, nos indica que los estudiantes razonan de la siguiente manera: si todos escogen 50 voy a poner 25…, pero si todos están pensando igual que yo entonces voy a escribir 12 (o 13) …, pero si todos siguen esta línea de razonamiento entonces mejor me voy con el 6 (o 7)… Generalmente los estudiantes llegan hasta allí; sin embargo, el razonamiento puede continuar un par de pasos adelante y llegar hasta el valor óptimo de 1 (o 2)…
Con esta información, ¿qué número escribiría en el papel?, ¿todos los estudiantes colocarían el mismo número?, ¿qué ocurre si repetimos varias veces este juego? Note que la respuesta a estas preguntas requiere pensar sobre qué harán los demás y eso es justamente lo que diferencia a la teoría de juegos de otras disciplinas que estudian los procesos de toma de decisiones.
Formalmente podemos decir que la teoría de juegos es una disciplina que estudia la manera como los individuos racionales toman decisiones estratégicas, es decir, considerando las posibles acciones de sus contrincantes; como en nuestro ejemplo introductorio, donde la decisión sobre qué número escribir en el papel depende de lo que creemos que colocarán los demás.
La teoría de juegos es una disciplina importante. Prueba de ello es que cerca de un tercio de los últimos premios Nobel de economía han tenido algo que ver con el desarrollo de tales ideas. Sin embargo, es una disciplina relativamente joven comparada con otros paradigmas económicos, pues su origen, puede decirse, se remonta a 1944 con la publicación del libro Games and Economic Behavior del matemático (¡y genio!) John Von Newman1 y el economista Oskar Morgenstern.
El objeto de estudio de la teoría de juegos no son realmente “juegos” como comúnmente los conocemos; por el contrario, en este libro un “juego” es cualquier interacción estratégica entre dos o más personas. Los ejemplos de los “juegos” que se analizan aquí se focalizan en interacciones gerenciales estratégicas: imagine un gerente de finanzas que está considerando recortar un dividendo para financiar un proyecto de inversión… ¿se puede justificar de manera creíble ese recorte?, ¿cómo reaccionará el mercado al momento del anuncio?
O considere dos contratistas petroleros que entran en un proceso de licitación para explorar en una determinada zona geográfica donde las condiciones de la oferta se fundamentan en la fracción de las ganancias que cada empresa ofrece como regalías a la estatal petrolera; entonces, ¿cuál es el mejor curso de acción para cada una de las empresas, considerando que entre mayor sea la regalía más probabilidades tienen de ganar la licitación pero a costa de reducir los márgenes de ganancia?
Adelante se formaliza aún más el concepto, pero, por ahora: si una determinada interacción estratégica tiene al menos dos “jugadores”, cada jugador tiene un conjunto de “estrategias” o planes de acción, y la interacción genera “pagos”, entonces estamos hablando de un “juego”.
También es importante entender que no necesariamente el análisis de un juego nos va a indicar qué va a suceder en la situación observada, pues ese no es el objetivo de la teoría de juegos; más bien lo que se busca es comprender mejor ciertas situaciones como, por ejemplo, el siguiente caso:
Un experto en juegos se reunió en una sala de juntas con un grupo de ejecutivos de finanzas y les propuso subastar un billete de 100 dólares. La regla de la subasta era que ganaba aquel que ofreciera más por el billete pero pagaba el que hiciera la segunda mejor oferta… ¿Por cuánto subastaron el billete? Bueno, ¡terminaron pagando 465 dólares por un billete de 100 dólares!
¿Cómo puede ocurrir esto entre ejecutivos bien entrenados en finanzas? Si el ejecutivo A dice que pagará 100 por el billete, el ejecutivo B dice entonces que pagará 110 y en ese caso se lleva el billete, mientras que el ejecutivo A paga los 100… pero el ejecutivo C viendo la situación ofrece 120, se lleva el billete y paga el ejecutivo B 110… Lo anterior sucedió de manera sucesiva hasta que el juego paró y el experto en juegos se llevó 465 dólares por el billete de 100.
Entonces, el objetivo de la teoría de juegos es entender más que predecir. Por eso es tan útil en prácticamente todas las áreas de conocimiento. Inclusive existen algunos economistas que argumentan que la teoría de juegos es realmente la teoría unificada de las ciencias sociales (Luce y Raiffa, 1989).
Aquí estudiaremos juegos sencillos que permiten entender situaciones complejas de la vida real, pero sin el aparato económico-matemático de los libros tradicionales sobre el tema. Para el lector interesado en comprender los fundamentos teóricos de la teoría de juegos recomendamos consultar diferentes textos, entre ellos Gibbons (1992), Dutta (1999), Rasmussen (2007), Dixit y Balebuff (2010), Pérez, Jimeno y Cerdá (2004), y Binmore (1994) representan exposiciones que si bien tienen un enfoque más técnico, son accesibles para un lector con conocimientos universitarios de matemáticas y economía; para aquellos lectores más interesados en los formalismos remitimos a Fudenberg (1991), Vega-Redondo (2003), Tirole (2006) y los handbooks de Aumann y Hart (1992, 1994 y 2002); en cuanto a los libros de texto editados en Colombia, y que presentan un enfoque técnico, resaltamos los de Monsalve y Arévalo (2005), y Özak (2006). Todas esas publicaciones son consideradas fundamentales y abordadas por especialistas en la materia. Por lo tanto, esta obra constituye un aporte que les permite a los actuales y futuros gerentes acercarse a la aplicación de la teoría de juegos en la toma de decisiones, sin necesidad de tener un conocimiento profundo matemático o económico, pero sin desconocer tampoco los elementos fundamentales de esas disciplinas, así como las limitaciones de esta teoría en la solución de problemas concretos en el ámbito gerencial.
Cada capítulo presenta una breve introducción teórica acerca de las distintas categorías de juegos que se van a estudiar, luego se analizan juegos abstractos (sin historias) para entender los conceptos presentados, posteriormente se abordan aplicaciones (juegos con historias) donde se busca enfrentar al lector a situaciones de la vida cotidiana que pueden ser analizadas como juegos estratégicos, después se incluyen problemas resueltos con los cuales se busca afianzar los conceptos aprendidos mediante la explicación paso a paso de cómo hallar e interpretar equilibrios y, finalmente, se introducen problemas sugeridos que incluyen tanto juegos abstractos como situaciones reales que deben ser analizados como juegos estratégicos.
Hemos dividido los juegos en dos categorías: juegos estáticos, donde cada jugador no sabe cómo jugó su contrincante, o donde ambos juegan simultáneamente (caps. 1, 2 y 5), y juegos dinámicos, donde los jugadores compiten secuencialmente (caps. 3, 4 y 6). Dentro de esta categorización estudiamos los juegos de información completa (caps. 1, 2, 3 y 4), en los cuales todos los jugadores tienen la misma información sobre los pagos de su contrincante, y los juegos de información incompleta, donde existe incertidumbre en alguno de los jugadores sobre los pagos de sus adversarios (caps. 5 y 6). Además, incorporamos un capítulo dedicado a las opciones reales, por la trascendencia que pueden tener en la valoración de un proyecto y de oportunidades de inversión que en general agregan valor a las empresas (cap. 7). El último capítulo ofrece una colección de trece minicasos que representan situaciones en contextos reales, donde se busca que el lector utilice las herramientas aprendidas a lo largo del texto.
Como lo definimos previamente, un juego representa una interacción estratégica entre al menos dos contrapartes. Pero si quisiéramos una definición apropiada de la teoría de juegos podemos remitirnos a los aportes de Martin Shubik, profesor de Princeton University a mediados del siglo pasado. Para Shubik (1955) la teoría de juegos estudia la toma de decisiones en situaciones de conflicto, es decir, situaciones en las cuales una sola persona no tiene el control total de todos los factores que afectan el resultado. El autor ofrece diferentes ejemplos, como el de los generales que dirigen sus ejércitos en una confrontación, los jugadores de póquer, y los políticos que buscan obtener una posición sometiéndose a elección popular. Todos esos “juegos”, y la toma de decisiones que los subyace, son objeto de estudio en la teoría de juegos.
Shubik sostiene que los problemas que se estudian en esta teoría son más complejos que un simple proceso de maximización. El jugador, o tomador de decisiones, busca obtener lo máximo que le sea posible, siendo consciente de que los demás persiguen también sus propios objetivos y que sus acciones afectan el resultado final que todos alcanzan; por lo tanto, debe tener en cuenta las posibles acciones y reacciones de los demás actores involucrados en el juego.
Decidimos traer a este texto los aportes de Shubik (1955) porque para él la teoría de juegos tiene una aplicación directa en la toma de decisiones gerenciales; por ejemplo, considera que dos compañías se enfrentan a duelo en diferentes ocasiones, de forma que en aquellos mercados que han alcanzado cierta madurez y cuyo tamaño se ha estabilizado, los nuevos clientes que logra conquistar una empresa implican una pérdida para su competidora, es decir, las firmas son oponentes claros ya que lo que gana una lo pierde la otra. Igual sucede cuando dos refinerías comparten el mismo mercado con una demanda relativamente fija. De acuerdo con Shubik, utilizando juegos más complejos que no son de suma cero, es posible dilucidar la propuesta que debe hacer una empresa que compite contra otros oferentes por contratos que licita el gobierno. Lo anterior, suponiendo que la empresa no cuenta con la capacidad instalada para atender más que un porcentaje de los proyectos, digamos un 30%, por lo que la oferta que hace la empresa debe modelarse para perder aproximadamente el 70% de los contratos debido a un precio menos competitivo que el de sus pares en el mercado.
Ahora bien, según Shubik (1955), las aplicaciones en el mundo empresarial no se limitan exclusivamente a nivel empresa; por ejemplo, al momento de expedir regulaciones relacionadas con la libre competencia, potenciales colusiones entre competidores, creaciones de carteles, y otras prácticas de competencia desleal, es posible modelar el comportamiento de los tomadores de decisiones en cada empresa a partir de la teoría de juegos. De igual manera, dentro de cada empresa, en unidades de análisis más pequeñas, se presentan situaciones que se pueden examinar a través de la teoría de juegos, tales como el poder de una persona al interior de un comité que le señala un comportamiento o relación no lineal con los votos que controla y las coaliciones que puede llegar a concretar.
Diversos estudios académicos validan la posición clásica de Shubik (1955). Por ejemplo, Saloner (1991) analiza la utilidad de la modelación que se puede realizar a través de la teoría de juegos para la gerencia estratégica; para él una gran cantidad de asuntos relacionados con la estrategia y la competitividad de las empresas puede modelarse y analizarse a través de la teoría de juegos, entre ellos la importancia de las ventajas para quien realiza el primer movimiento, el papel del compromiso estratégico cuidando una participación en el mercado, la construcción de una reputación, la señalización al mercado, y el control estratégico de la información.
Pero no solo las estrategias externas se pueden analizar con esta batería de herramientas. Los tomadores de decisiones pueden apoyarse en la teoría de juegos para resolver asuntos relacionados con la estrategia interna de la empresa, entre ellos los esquemas de incentivos, la integración vertical, la composición de los comités ejecutivos, y la asignación de poder formal a diferentes niveles organizacionales. Saloner hace una aclaración que es totalmente válida para el lector de este texto: los juegos que se plantean alrededor de asuntos estratégicos y gerenciales tienen una limitante representada en la racionalidad de los jugadores o tomadores de decisiones, de forma que la efectividad del uso de la teoría de juegos en el contexto gerencial depende de cuáles sean las expectativas de los ejecutivos respecto del papel de las herramientas que provee esta teoría.
Si se quieren tomar decisiones muy específicas en respuesta a interrogantes tales como cuánta debe ser la capacidad instalada, cómo posicionar un producto y cuánto producir, la teoría de juegos se puede ver desafiada por la dificultad de modelar la racionalidad del tomador de decisiones. Sin embargo, es posible encontrar diferentes juegos aplicados a la toma de decisiones gerenciales donde el nivel de plausibilidad de las conclusiones no se ve amenazada por la modelación de la racionalidad. En general los juegos proveen intuición, permiten al ejecutivo evidenciar las tensiones, tratar de anticipar la reacción de las contrapartes involucradas y tomar una mejor decisión. Además, para Saloner la teoría de juegos permite a la empresa no solo pensar en maximizar utilidades sino en obtener resultados óptimos en diferentes aspectos, monetarios o no monetarios, que tendrán impacto en su sustentabilidad a largo plazo.
Pulido, Sánchez-Soriano y Llorca (2002) analizan un caso particular que enfrenta la gerencia y que es común en las universidades: las tensiones que enfrentan las directivas cuando asignan recursos financieros para la compra de equipos técnicos destinados a los laboratorios de los diferentes departamentos. El problema particular surge cuando los recursos financieros limitados no logran satisfacer las demandas de los diferentes departamentos, y se hace más severo debido a que las demandas que realizan son altamente subjetivas. Pulido et al. desarrollan en detalle un modelo basado en teoría de juegos que explica el proceso de toma de decisiones que observan en su universidad y que puede servir de soporte para otros tomadores de decisiones.
Un estudio reciente de Peldschus (2008) resalta la importancia y aplicabilidad de la teoría de juegos para la alta gerencia de las empresas dedicadas a la construcción. El autor asegura que ese sector se ve afectado por decisiones complejas que se deben tomar con información incompleta respecto de factores determinantes como la adquisición de maquinaria y herramientas, la implementación de procesos, la contratación de personal y en general, la coordinación de todos esos elementos para alcanzar el mayor resultado posible con los limitados recursos financieros a disposición.
Sin embargo, tales características del proceso de toma de decisiones en ese sector, por demás evidentes, son regularmente ignoradas por los ejecutivos a cargo del despliegue operativo y del desarrollo de la estrategia, por lo que la toma de decisiones se basa en modelos simples que se adaptan parcialmente de acuerdo con las experiencias del equipo de alta gerencia y los resultados de la empresa, pero que no reflejan de manera adecuada la situación a enfrentar. Peldschus asegura que a través de esos métodos se llega a soluciones que se pueden implementar y que son viables, pero que no necesariamente representan la mejor opción para las empresas.
La posibilidad de representar situaciones con diversas tensiones y sus potenciales soluciones permite escoger el comportamiento más favorable entre un conjunto de comportamientos posibles, así el autor presenta soluciones a problemas cotidianos a través de las herramientas ofrecidas por la teoría de juegos.
Podríamos ofrecer ejemplos adicionales, pero con las investigaciones aquí reseñadas es posible resaltar el valor de la teoría de juegos, reconocida en la literatura por más de seis décadas, y su aplicación directa al entorno empresarial, especialmente por aquellos a cargo del proceso de toma de decisiones gerenciales y estratégicas.
Veamos un juego clásico conocido como el juego de la guerra fría, e introduzcamos las definiciones básicas para que una situación dada se convierta en un juego, a saber: jugadores, estrategias, pagos y equilibrio.
Considere la situación entre Estados Unidos y la Unión Soviética durante el período 1945-1985. En nuestro contexto cada país representa un jugador y ambos tienen dos posibles estrategias: lanzar un ataque nuclear (A), o no hacerlo (NA). Si los dos países atacan simultáneamente el resultado sería la destrucción total del mundo; si uno solo ataca, el país atacado quedará totalmente destruido, pero el otro deberá asumir los costos ambientales del ataque, que, supongamos, puede representarse por una cantidad C. En caso de que ninguno de los dos decida atacar, cada uno deberá invertir un monto importante de dinero (I) en armamento nuclear para que le quede claro a su rival que cuenta con suficiente poder destructivo. Supongamos que las inversiones requeridas en armamento son menores que los costos ambientales de un ataque nuclear.
Antes de seguir es importante dejar en claro la diferencia entre acciones y estrategias. En este caso, dado que estamos suponiendo un juego estático donde los dos jugadores juegan simultáneamente, las acciones y las estrategias representan exactamente el mismo conjunto: (A, NA); sin embargo, las acciones representan hechos físicos (qué botón accionar si la decisión es atacar) mientras que las estrategias representan planes sobre qué hacer en determinadas circunstancias. Más adelante, cuando introduzcamos los juegos secuenciales, quedará más clara la diferencia entre acciones y estrategias; por ahora lo importante es entender que las estrategias representan “planes” de acción.
Generalmente la situación planteada se puede representar gráficamente con una matriz como la siguiente:
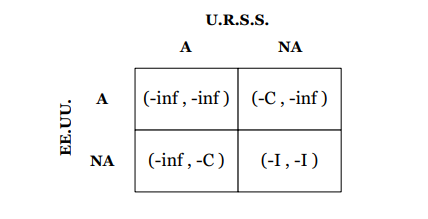
Note que, de acuerdo con lo definido, la matriz representa un juego, ya que claramente se establece quiénes son los jugadores (Estados Unidos y la Unión Soviética), cuáles son sus estrategias (Atacar o No Atacar) y cuáles son los pagos para cada situación posible dentro del juego (p. ej., destrucción total si los dos atacan, lo cual genera un pago de menos infinito ya que los dos países quedan totalmente destruidos).
Por otra parte, cuando se representa un juego en forma de matriz, es una convención usual que el jugador 1 esté a la izquierda (Estados Unidos en este caso) y el jugador 2 en la parte de arriba de la matriz (la Unión Soviética, en este caso). El primer número dentro de cada cuadrante representa el pago2 del jugador 1 y el segundo representa el pago del jugador 2 (Pago Jugador 1, Pago Jugador 2). Por ejemplo, si Estados Unidos decide no atacar mientras que la Unión Soviética sí lo hace, el pago correspondiente a cada jugador sería de menos infinito para el primer jugador dado que queda destruido, y el pago para el jugador que ataca sería el costo ambiental generado por la decisión de atacar (-inf, -C).
Este juego permite entender el concepto de equilibrio. Se habrá alcanzado una situación de equilibrio cuando a ninguno de los jugadores le conviene moverse. Otra forma de entenderlo es cuando cada jugador escoge la estrategia óptima dado que sus contrincantes también escogieron sus estrategias óptimas. Como cada uno está optimizando su conjunto de estrategias ninguno querrá salir de esa situación, por lo que en consecuencia se dice que el juego llegó a un equilibrio3.
Veamos si el juego de la guerra fría llega a un equilibrio. Para hacerlo cada jugador supone las distintas estrategias de su contrincante y trata, dado su propio conjunto de estrategias, de escoger aquellas que maximicen su pago. Note que los jugadores no están tratando de “ganar el juego” sino de “maximizar sus pagos”.
Por ejemplo, para el caso del juego de la guerra fría, ¿cuál será la estrategia óptima de la Unión Soviética si Estados Unidos ataca? Utilizando la matriz de pagos encontramos lo siguiente:
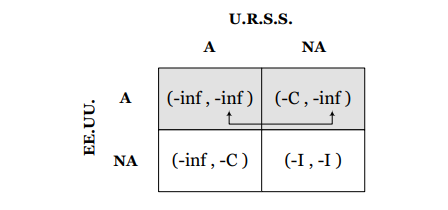
En este caso para la Unión Soviética es indiferente atacar o no atacar debido a que de todas formas quedará totalmente destruida. Supongamos que en caso de “empate” se toma la decisión de atacar también. ¿Qué hará la Unión Soviética si Estados Unidos decide no atacar? Utilizando la matriz de pagos encontramos lo siguiente:
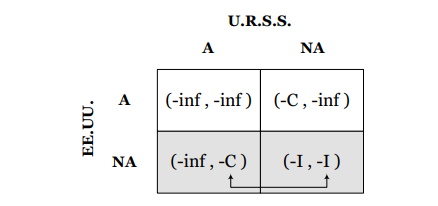
Note que en esta situación la Unión Soviética debe comparar entre los costos ambientales de atacar a Estados Unidos versus las inversiones requeridas en armamento. Como hemos supuesto que C es mayor que I, entonces la Unión Soviética decide, maximizando sus pagos, no atacar.
El mismo análisis lo hacemos análogamente para el caso en que Estados Unidos debe decidir qué hacer dadas las distintas estrategias de la Unión Soviética, tal como se muestra en la siguiente matriz:
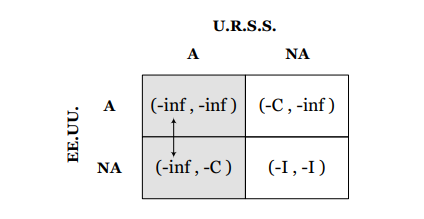
Si la Unión Soviética decide atacar, para Estados Unidos es indiferente llevar a cabo cualquier estrategia dado que sus pagos serían los mismos.
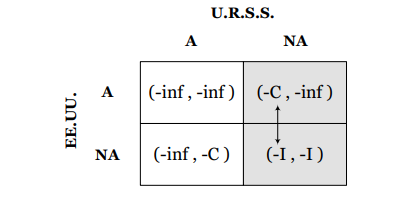
Pero si la Unión Soviética decide no atacar, Estados Unidos desarrollará un análisis relacionado con la maximización de sus pagos. Bajo el supuesto de que la inversión realizada en armamento nuclear sea inferior al costo ambiental que genera la destrucción del país, Estados Unidos decidirá igualmente no atacar.
Note que luego de hacer las respectivas comparaciones de pagos para cada uno de los jugadores dadas las posibles estrategias de su contrincante, llegamos al cuadrante (-I, -I) donde ninguno de los jugadores ataca y los dos prefieren invertir en armamento nuclear:
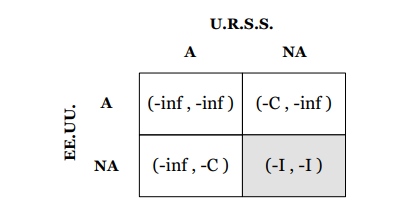
A ese equilibrio se le llamó “guerra fría”.
Mucho de lo que se hace en este libro es justamente buscar e interpretar equilibrios, es decir, encontrar interacciones estratégicas que conduzcan a situaciones donde ninguno de los jugadores tenga incentivos para desviarse, es decir, situaciones de equilibrio.
Otro concepto importante que se desprende del juego de la guerra fría es el de common knowledge..